Раздел 2 Методические указания по изучению содержания тем и разделов дисциплины

 

2 .1 Задача С1. Плоская система сил

 

Жесткая шарнирная рама (рисунок С1.0 – С1.9) закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню в шарнирами на концах, или к шарнирной опоре на катках.

В точке С к раме привязан трос, который перекинут черев блек и несет на конце груз Р = 25 кН. На раму действует пара сил с моментом M = 60 кН*м и две силы, величины, направления и точки приложения которых указаны в таблице С1.

Определить реакции связей в точках А и В, вызываемые действу­ющими нагрузками. При окончательных расчетах принять a = 0,5 м.

 

Таблица С1 Данные к задаче С1

Силы	α1 F1 = 10 кН	α2 F2 = 20 кН	α3 F3 = 30 кН	α4 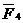F4 = 40 кН
Номер условия	Точка приложения	α1	Точка приложения	α2	Точка приложения	α3	Точка приложения	α4
	H	30	–	–	K	45	–	–
	–	–	D	30	H	60	–	–
	K	75	–	–	–	–	E	30
	–	–	K	60	H	30	–	–
	D	30	–	–	–	–	K	60
	–	–	H	30	D	75	–	–
	–	–	E	45	–	–	K	30
	–	–	D	60	H	30	–	–
	K	60	–	–	–	–	E	45
	–	–	K	75	–	–	H	30

 

 

 

 

Пример С1 Жесткая шарнирная рама АНСВ (рисунок С1) имеет в точке А шарнирную опору, а в точке В – подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.

Дано: а=0,5м; F₂=20кН; F₄=40кН; M=60кНм, Р=25кН

Определить: реакции связей в точках А и В, вызываемые действующими нагрузками.

Решение.1. Рассмотрим равновесие рамы. Проведем координатные оси xy и изобразим действующие на пластину силы: силу F, пару сил с моментами М, натяжение троса Т и реакции связей XА, YА, RВ (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).

Рис.С1

2. Для полученной плоскости системы сил составим три уравнения равновесия. При вычислении момента силы F относительно токи А воспользуемся теоремой Вариньона, т.е. разложим силу F на составляющие.

Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.

 

 

2.2 Задача С2. Пространственная система сил

 

Найти реакции опор заданной конструкции. Необходимые для вычислений значения сил Q, G и размеров взять из таблицы С2.

 

Таблица С2 Данные к задаче С2

Номер условия	Q, H	G, H	a, м	b, м	c, м	R, м	r, м
	200	100	0,2	0,3	0,1	0,15	0,08
	300	150	0,3	0,2	0,15	0,18	0,1
	400	250	0,25	0,2	0,15	0,15	0,07
	350	200	0,3	0,25	0,2	0,1	0,07
	250	150	0,25	0,15	0,15	0,12	0,08
	250	200	0,2	0,25	0,15	0,12	0,07
	400	300	0,3	0,3	0,2	0,2	0,12
	150	250	0,2	0,25	0,15	0,12	0,08
	200	150	0,25	0,2	0,1	0,12	0,1
	350	300	0,2	0,25	0,15	0,15	0,1

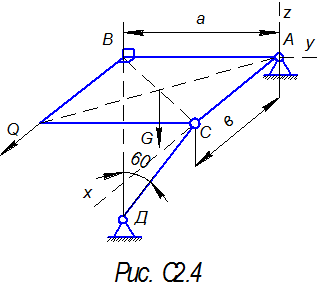
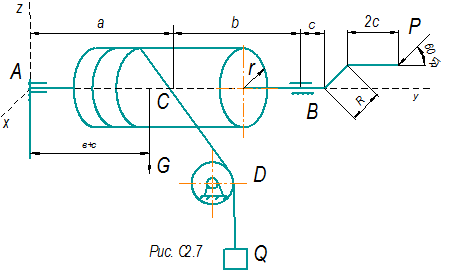
Пример С2 Заданная однородная прямоугольная плита весом G=150Н и силой Q=250H, со сторонами a=0,25м, b=0,15м, закреплена в точке А сферическим шарниром, а в точке В цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем СD.

Определить реакции опор в точках А и В, и стержне СD

Размеры указаны на чертеже.

Дано: G=150Н, Q=250H, a=0,25м, b=0,15м,.

Решение 1. Рассмотрим равновесие плиты. На нее действуют заданные силы G, Q, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие XA, YА, ZА, цилиндрического (подпятника) – на две составляющие XВ, ZВ, и реакцию Rc стержня направив вдоль стержня, предлагая, что он сжат.

2. Для определения шести неизвестных реакций составим шесть уравнений равновесия действующей на плиту пространственной системы сил:

 

Рис.2

 

Находим неизвестные из уравнений

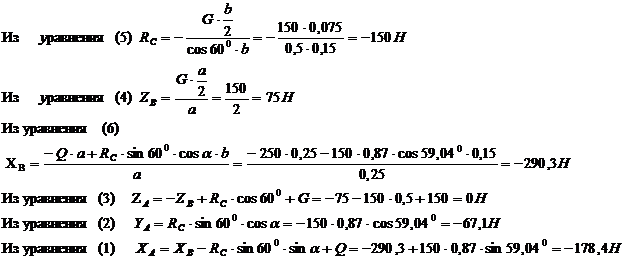
2.3 Задача К1. Кинематика точки

 

Точка М движется в плоскости xy согласно заданным уравнениям x = x(t) и y = y(t) (таблица К1), где x и y выражены в сантиметрах, t – в секундах.

Найти уравнение траектории точки; для момента времени t₁ = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории. Построить в масштабе чертеж траектории, указать положение точки М и все вектора.

 

Таблица К1 Уравнения движения точки М по осям координат

 

Предпоследняя цифра шифра	х = х(t)	Последняя цифра шифра	y = y (t)
	–2t2 + 3		–5t
	4t2 – 2t + 1		3t
	–3cos(πt/3) + 2		4t
	2sin(πt/3)		–2t
	3t2 + 2		2t
	7sin(πt/6) + 3		–3t
	–3/(t + 2)		–4t
	–4cos(πt/3)		5t
	3t2 + t + 3		2t
	6sin(πt/6) – 2		–3t

 

Пример К1. Даны уравнения движения точки в плоскости xy: 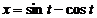, Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени _.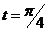

Решение: Для определения уравнения траектории точки исключим из заданных уравнений движения время t.

Скорости точки:

,

,

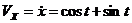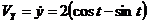Модуль скорости:

Ускорения точки:

,

,

Модуль полного ускорения:

Модуль касательного ускорения точки:

,

А модуль нормального ускорения:

.

Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

 

2.4 Задача К2. Сложное движение точки. Теорема Кориолиса

 

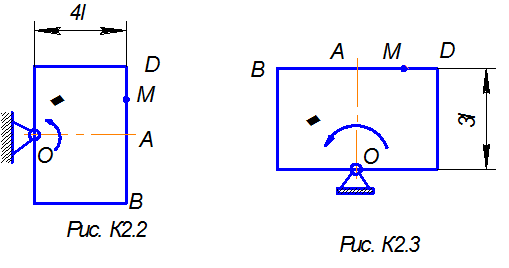
Прямоугольная пластина (рисунок К2.0 – К2.4) или круглая пластина радиуса R = 60 см (рисунок К2.5 – К2.9) вращается вокруг неподвижной оси по закону φ = φ(t), заданному в таблице К2. На рисунке 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины, на остальных рисун­ках ось вращения лежит в плоскости пластины.

По пластине вдоль прямой BD (рисунок К2.0 – К2.5) или по окруж–ности (рисунок К2.6 – К2.9) движется точка М; закон ее относительного движения s = AM = s(t) см.

Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t₁ = 1 с.

 

 

Таблица К2 Данные к задаче К2

 

Номер условия	Для всех рисунков φ(t), рад	Для рисунков 0 – 5	Для рисунков 6 – 9
b, см	s(t)	l	s(t), см
	4(t2 – t)	12	50(3t – t2) – 64	R	(π/3)R(4t2 – 2t3)
	3t2 – 8t	16	40(3t2 – t4) – 32	(4/3)R	(π/2)R(2t2 – t3)
	6t3 – 12t2	10	80(t2 – t) + 40	R	(π/3)R(2t2 – 1)
	t2 – 2t3	16	60(t4 – 3t2) + 56	R	(π/3)R(t4 – 3t2)
	10t2 – 5t3	8	80(2t2 – t3) – 48	R	(π/6)R(3t – t2)
	2(t2 – t)	20	60(t3 – 2t2)	R	(π/3)R(t3 – 2t)
	5t – 4t2	12	40(t2 – 3t) + 32	(3/4)R	(π/2)R(t3 – 2t2)
	15t – 3t2	8	60(t – t3) + 24	R	(π/6)R(t – 5t2)
	2t3 – 11t	10	50(t3 – t) – 30	R	(π/3)R(3t2 – t)
	6t2 – 3t3	20	40(t – 2t2) – 40	(4/3)R	(π/2)R(t – 2t2)

 

 

 

 

Пример К2. Круглая пластина R = 60 см вращается вокруг неподвижной оси по закону . По дуге окружности R движется точка по закону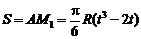

Дано: R=60 см; ; l =R; ; t ₁= 1 c.

Определить: V_абс и a _абс.

Указания. Задача – на сложное движение точки. Для ее решения следует воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, необходимо по условиям задачи определить, где находится точка М на пластине в момент времени t ₁ =1 с, и изобразить точку именно в этом положении (а не в произвольном, как показано на рисунках к задаче).

Решение.Рассмотрим движение точки М как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам:

,

,

где ,

.

Определим все входящие в равенство величины.

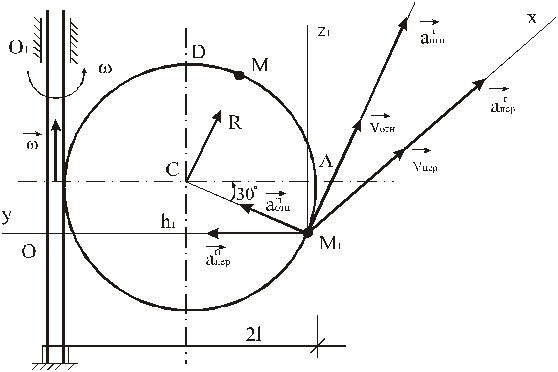1. Относительное движение

Рис.К2

 

Это движение происходит по закону

.

Установим, где будет находиться точка М на дуге окружности в момент времени t ₁, полагая, что t ₁ = 1 c:

.

Знак «минус» свидетельствует о том, что точка М в момент времени t ₁=1 c находится снизу от точки А. Изображаем ее в этом положении: .

Находим числовые значения , :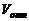

м/с.

м/с².

м/с².

Вектор направлен к центру C окружности, векторы и 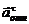направлены в сторону положительного отсчета.

2. Переносное движение

Это движение происходит по закону .

Найдем сначала угловую скорость и угловое ускорение переносного вращения:

, ,

при t ₁ = 1 c, 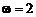c^-1, c^-2.

Для определения находим сначала расстояние h₁ =О^/М₁ точки М₁ от оси вращения.

СК =Rcos30⁰ =0,52 м, ОК =СК + R =1,12 м, М₁О^/ = ОК=1,12 м.

Находим: =224 см/с, =448 см/с²,

=448 см/с².

Изобразим векторы и перпендикулярно плоскости DAO^/, а вектор – по линии МO^/ к оси вращения.

3. Кориолисово ускорение

Т.к. угол между вектором и осью вращения (вектором ) равен 30⁰, то численно в момент времени t ₁ =1 с

=2·0,31·2·(1/2) =0,68 см/с².

Направление найдем по правилу Жуковского. Для этого вектор спроектируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору ), и затем эту проекцию повернем на 90⁰ в сторону , т.е. против хода часовой стрелки. Получим направление вектора . Он направлен перпендикулярно плоскости пластины так же, как и вектор .

4. Определение V _абс и а _абс Т.к. , а векторы и взаимноперпендикулярны, то

= 234 см/с.

По теореме о сложении ускорений

.

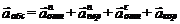Для определения а _абс проведем координаты М₁хуz и вычислим проекции а _абс на эти оси. Векторы и лежат на оси х, а векторы и расположены в плоскости М₁уz₁, т.е. в плоскости пластины.

Проецируя обе части равенства на оси М₁хуz, получаем:

а _{абс х} = =448,62 см/с²,

а _{абс z} = · =1,71 см/с²,

а _{абс у} = =449,08 см/с².

Находим затем а _абс. а _абс = =634,8 см/с².

Ответ: V _абс =234 см/с; a _абс =634,8 см/с².

 

2.5 Задача КЗ. Плоскопараллельное движение твердого тела

 

Для заданного положения механизма найти незаданные угловые скорости и ускорения звеньев механизма, а также скорости и ускорения точек В и С.

 

Таблица К3 Данные к задаче К3

Номер условия	Размеры, см	ω0, с–1	ε0, с–2
ОА	АВ	АС
	50	100	30	4	5
	40	80	30	3	6
	35	75	25	–5	7
	30	70	30	3	6
	40	100	50	3	–5
	20	70	30	2	4
	25	75	25	–3	5
	40	100	40	3	–5
	15	50	20	4	6
	45	120	40	2	–4

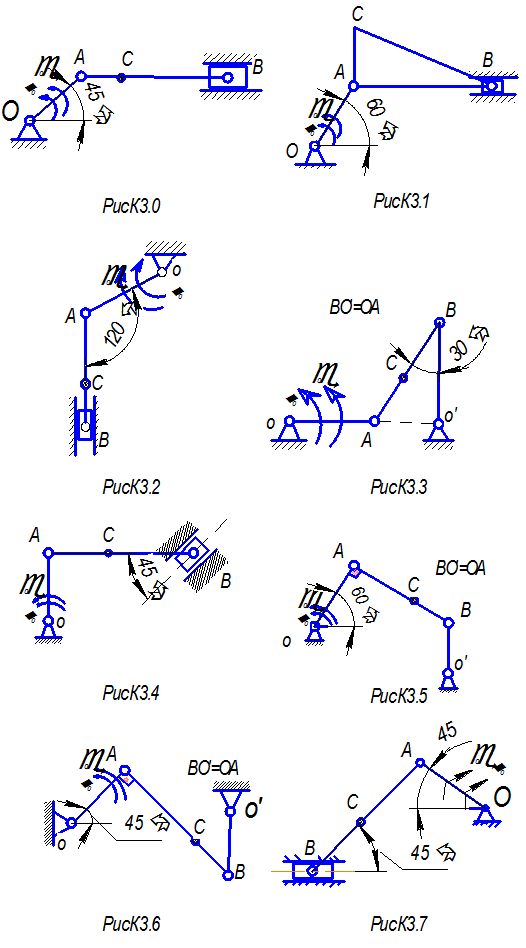
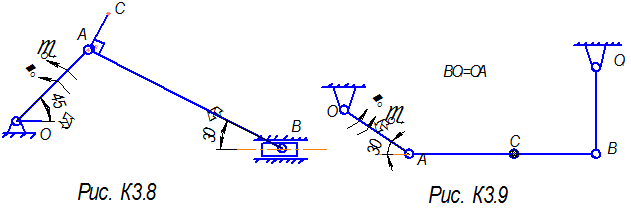
Пример К3. Найти для заданного положения механизма скорости и ускорения точек B и C, а также угловую скорость и угловое ускорение звена, которому эти точки принадлежат.

Дано: Cхема механизма в заданном положении (рис.К3.1), исходные данные таковы, что OA = 40 см, AC = 20 см, ω_OA = 5 рад/с, ε_OA = 10 рад/с².

Найти: .

Решение: 1) Определение скорости точек и угловой скорости звена AB: вычисляем модуль скорости точки A при заданном положении механизма:

.

Скорость точки А перпендикулярна кривошипу ОА. Скорость ползуна В направлена вдоль ОВ. Мгновенный центр скоростей P_AB шатуна АВ находится в точке пересечения перпендикуляров, проведенных из точек A и B к их скоростям.

Угловая скорость звена AB:

.

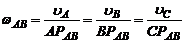Расстояния АР_АВ, ВР_АВ и СР_АВ определяются из рассмотрения треугольников АСР_АВ и АВР_АВ :

AP_АВ=OA =40 см, ВP_АВ= см, СP_АВ= см.

В соответствии с этим , ; ; .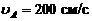

Вектор направлен перпендикулярно отрезку СР_АВ в сторону, соответствующую направлению вращения звена АВ.

2) Определение ускорений точек и углового ускорения звена AB(рис.К.3.2). Ускорение точки A складывается из вращательного и центростремительного ускорений:

,

где , .

Согласно теореме об ускорениях точек плоской фигуры:

или . (1)

Вектор направлен от A к О. Вектор перпендикулярен вектору и направлен в сторону, противоположную , (т.к. из условия задачи движение кривошипа OA замедленное).

Центростремительное ускорение точки B во вращательном движении шатуна AB вокруг полюса A: и направлено от B к A.

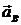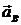Ускорение направлено вдоль линии OB, а . Зададим произвольно их направления: - вертикально вверх, - от B к O. Эти ускорения определим из уравнений проекций векторного равенства (2) на оси координат. Знак в ответе показывает, соответствует ли истинное направление вектора принятому при расчете.

Выбрав направление осей x и y, как показано на рис.К3.2, получаем:

, (2)

. (3)

Из уравнения (2) находим

.

Из уравнения (3) получаем

.

Следовательно, ускорение 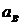направлено так, как показано на рисунке, а – в противоположную сторону. Истинная картина ускорений для точки B показана на рис.К.3.3.

Угловое ускорение шатуна AB: .

Направление относительно полюса A определяет направление углового ускорения 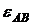. В данном случае, 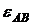не совпадает с направлением , следовательно, движение звена замедленное.

Определим ускорение точки C:

.

Вращательное и центростремительное ускорения точки C во вращательном движении AB вокруг полюса A:

;

.

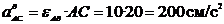Вектор 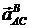перпендикулярен вектору и направлен соответственно угловому ускорению .

Ускорение находим методом проекций (рис.К3.4):

, ,

.

В результате вычислений получаем:

,

,

 

 

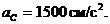
2.6 Задача Д1. Дифференциальные уравнения движения материальной точки

 

Груз D массой m, получив в точке A начальную скорость υ₀, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости. На участке АВ на груз кроме силы тяжести действуют постоянная сила и сила сопротивления среды, зависящая от скорости груза и направленная против движения.

В точке В груз, не изменяя значения своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует пе­ременная сила , проекция которой F_x на ось x задана в таблице Д1.

Считая груз материальной точкой и зная расстояние АВ = l или время t₁ движения груза от точки А до точки В, найти закон движе­ния груза на участке ВС в виде функции x = f(t). Трением пренеб­речь.

 

Таблица Д1 Данные к задаче Д1

 

Номер условия	m, кг	υ0, м/с	Q, Н	R, Н	l, м	t1, с	Fx, Н
	2,4	12	5	0,8υ2	1,5	–	4sin(4t)
	2	20	6	0,4υ	–	2,5	–5cos(4t)
	8	10	16	0,5υ2	4	–	6t2
	1,8	24	5	0,3υ	–	2	–2cos(2t)
	6	15	12	0,6υ2	5	–	–5sin(2t)
	4,5	22	9	0,5υ	–	3	3t
	4	12	10	0,8υ2	2,5	–	6cos(4t)
	1,6	18	4	0,4υ	–	2	–3sin(4t)
	4,8	10	10	0,2υ2	4	–	4cos(2t)
	3	22	9	0,5υ	–	3	4sin(2t)

 

 

Пример Д1. На наклонном участке AB трубы на груз D массы m действуют сила тяжести P, сила сопротивления R и сила трения _.; коэффициент трения равен ; время движения груза от точки А, где , до точки В равно ; на вертикальном участке ВС на груз действуют сила тяжести и переменная сила F=F(t), заданная в ньютонах.

Рис. Д1

 

Дано: m=2 кг, R = 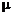v, где 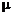= 0,5 кг/с, f=0,2, v₀=2 м/с, = = 2 c, =30°, .

Определить: закон движения груза на участке ВС, т.е. зависимость .

Указания. Задача — на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке , учтя начальные условия. Затем, зная время движения груза на участке или длину этого участка, определить скорость груза в точке 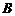. Эта скорость будет начальной для движения груза на участке . После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке 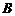, и полагая в этот момент . При интегрировании уравнения движения на участке в случае, когда задана длина 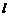участка, целесообразно перейти к переменному 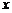, учтя, что

Решение: Рассмотрим движение груза на участке АВ. Выберем начало отсчета в точке А и направим ось А_z в сторону движения (рис. Д1-1). Тогда начальные условия будут: при . Изображаем в произвольном положении груз и действующие на него силы и (нормальная реакция трубы). Составляем дифференциальное уравнение движения груза в проекции на ось А_z:

или . (1)

Проекции сил имеют значения , .

, , и уравнение (1) примет вид

. (2)

Для определения N составим уравнение в проекции на ось А_y:

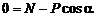
или

.

Подставим найденное значение N в уравнение (2) и, разделив обе части уравнения на m, получим:

. (3)

Обозначим и подсчитаем величины:

,

k= 10(0,5 – 0,2×0,866)= 3,27 м/с², (4)

, с^-1.

С учетом (4) уравнение (3) примет вид:

.

Разделяя переменные, запишем:

.

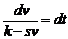Общее решение данного уравнения есть

(5)

Найдем постоянную интегрирования, используя начальные условия: при t=0, v = v ₀

.

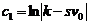Уравнение (5) теперь перепишется в виде:

,

откуда

.

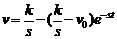При t=t₁, т.е. в точке В скорость груза равна

м/с.

Рассмотрим теперь движение груза на участке ВС. Выберем начало отсчета в точке В и направим ось В_х вертикально вниз. Будем считать, что при t=0, х=0, v_х= v₁. На груз действуют силы тяжести Р и переменная сила F, зависящая только от t. Дифференциальное уравнение движения груза в проекции на ось В_х имеет вид:

. (6)

Заметим, что в уравнениях (2) и (6) переменные силы выражены через величины, от которых они зависят. Обе стороны уравнения (6) поделим на m и запишем

. (7)

Уравнение (7) дважды последовательно интегрируем и, определяя из начальных условий постоянные интегрирования, находим искомую зависимость х=f(t):

. (8)

При t = 0, , .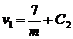

Подставляем найденное значение С₂ в (8), получим

откуда

. (9)

При t = 0 C₃ = 0.

Окончательно получим:

.

Подставив числовые значения величин m, g и v₁, получим закон движения груза в виде:

х=2,9t + 5,15t² + 3,5×sint, где t – в с, х – в м.

 

 

2.7 Задача Д2. Общие теоремы динамики механической системы

 

Механическая система состоит ив прямоугольной вертикальной плиты 1 массой m₁ = 24 кг и груза D массой m₂ = 8 кг; плита или движется вдоль горизонтальных направляющих (рисунок Д2.0 – Д2.4), или вращается вокруг вертикальной оси z, лежащей в плоскости плиты (рисунок Д2.5 – Д2.9). В момент времени t₀ = 0 груз начинает двигаться под действием внутренних сил по имеющемуся на плите желобу по закону s = AD = F(t), заданному в таблице Д2, где s вы­ражено в метрах, t – в секундах. Форма желоба или прямолинейная, или выполнена по окружности радиуса R = 0,8 м с центром в центре масс C₁ плиты.

Плита на рисунке Д2.0 – Д2.4 в начальный момент времени непод–вижна, а на рисунке Д2.5 – Д2.9 имеет начальную угловую скорость ω₀ = 8 с^-1 и в этот момент на нее начинает действовать вращающий момент М (момент относительно оси z), заданный в таблице в Н*м и направленный как ω₀ при М > 0 и в противоположную сторону при М < 0. Ось z проходит от центра С₁ плиты на расстоянии b; размеры плиты показаны на рисунках.

Считая груз материальной точкой и пренебрегая всеми сопротивлениями, определить указанные в таблице Д2 величины: х₁ – перемещение плиты за время от t₀ = 0 до t₁ = 1 c, U₁ – скорость плиты в момент времени t1, N1 – полную силу нормального давления плиты на направляющие в момент времени t1, ω1 – угловую скорость плиты в момент времени t1, ω = f(t) – угловую скорость плиты как функцию времени.

 

Таблица Д2 Данные к задаче Д2