Пусть дан ряд с положительными членами 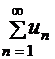 и существует предел
и существует предел  .
.
Тогда: 1) при С < 1 ряд сходится;
2) при С > 1 ряд расходится
(при С = 1 признак не дает ответа о сходимости ряда).
Пример 6. Исследовать ряды на сходимость:
а)  .
.
Решение. Общий член ряда 

 .
.
Вычислим 

 >
>  .
.
Следовательно, ряд расходится по радикальному признаку Коши.
Ответ: расходится.
б)  .
.
Решение. Общий член ряда 
 .
.
Вычислим 




 .
.
Следовательно, ряд сходится по радикальному признаку Коши.
Ответ: сходится.
в)  .
.
Решение. Общий член ряда 

 .
.
Вычислим







 .
.
Следовательно, ряд сходится по радикальному признаку Коши.
Ответ: сходится.
Интегральный признак Коши
Пусть дан ряд с положительными членами  такой, что члены ряда монотонно убывают
такой, что члены ряда монотонно убывают  и функция
и функция  , непрерывная при
, непрерывная при  такая, что
такая, что  .
.
Тогда  и несобственный интеграл
и несобственный интеграл  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример 7. Исследовать ряды на сходимость:
а)  .
.
Решение. Положим 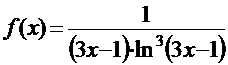 . Эта функция удовлетворяет всем требованиям интегрального признака Коши.
. Эта функция удовлетворяет всем требованиям интегрального признака Коши.
Рассмотрим несобственный интеграл.







 ― число.
― число.
Tак как несобственный интеграл сходится, то и исходный ряд сходится по интегральному признаку Коши.
Ответ: сходится.
б)  .
.
Решение. Положим  . Эта функция удовлетворяет всем требованиям интегрального признака Коши.
. Эта функция удовлетворяет всем требованиям интегрального признака Коши.
Рассмотрим несобственный интеграл
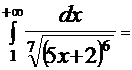


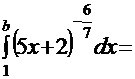



 .
.
Следовательно, несобственный интеграл расходится, тогда и ряд
 расходится по интегральному признаку Коши.
расходится по интегральному признаку Коши.
Ответ: расходится.
ЗНАКОЧЕРЕДУЮЩИЕСЯ ЧИСЛОВЫЕ РЯДЫ
Ряд вида 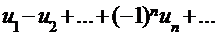 , где
, где  , называется знакочередующимся рядом. Для знакочередующегося ряда справедлива теорема Лейбница.
, называется знакочередующимся рядом. Для знакочередующегося ряда справедлива теорема Лейбница.
Теорема Лейбница
Если для знакочередующегося ряда 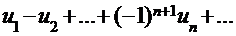 выполняется 1)
выполняется 1)  ; 2)
; 2)  , то ряд сходится и его сумма S удовлетворяет условию
, то ряд сходится и его сумма S удовлетворяет условию 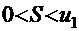 .
.
|
|
Наряду со знакочередующимся рядом  рассмотрим ряд из абсолютных величин
рассмотрим ряд из абсолютных величин  , члены которого – положительные числа. Если ряд из абсолютных величин
, члены которого – положительные числа. Если ряд из абсолютных величин  сходится, то знакочередующийся ряд
сходится, то знакочередующийся ряд  тоже сходится и
тоже сходится и  называется абсолютно сходящимся. Если ряд из абсолютных величин
называется абсолютно сходящимся. Если ряд из абсолютных величин  расходится, а знакочередующийся ряд
расходится, а знакочередующийся ряд  сходится (по теореме Лейбница), то
сходится (по теореме Лейбница), то  называется условно сходящимся.
называется условно сходящимся.
Исследовать знакочередующиеся ряды  на абсолютную и условную сходимость можно по следующей схеме:
на абсолютную и условную сходимость можно по следующей схеме:
1. Вычислить  . Если
. Если  , то ряд расходится по достаточному признаку расходимости и исследование этого ряда закончено.
, то ряд расходится по достаточному признаку расходимости и исследование этого ряда закончено.
2. Составить ряд из модулей  ― знакоположительный числовой ряд. Используя признаки сходимости рядов с положительными членами, исследовать его на сходимость. Если ряд из модулей
― знакоположительный числовой ряд. Используя признаки сходимости рядов с положительными членами, исследовать его на сходимость. Если ряд из модулей  сходится, то исходный знакочередующийся ряд
сходится, то исходный знакочередующийся ряд  сходится абсолютно и исследование этого ряда закончено.
сходится абсолютно и исследование этого ряда закончено.
3. Проверить выполнение условий теоремы Лейбница для знакочередующихся рядов. Если условия выполнены, то знакочередующийся ряд  сходится условно, если нет – то расходится.
сходится условно, если нет – то расходится.
Пример 8. Исследовать знакочередующиеся ряды на абсолютную и условную сходимость.
а)  .
.
Решение. Общий член ряда  .
.
1. Проверим  . Следовательно, исходный ряд расходится по достаточному признаку расходимости.
. Следовательно, исходный ряд расходится по достаточному признаку расходимости.
Ответ: расходится.
б)  .
.
Решение. Общий член ряда 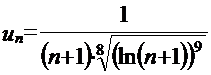 .
.
1. Проверим  .
.
2. Составим ряд из модулей  ― знакоположительный числовой ряд, и применим к нему интегральный признак Коши. Положим
― знакоположительный числовой ряд, и применим к нему интегральный признак Коши. Положим 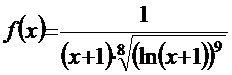 . Эта функция удовлетворяет требованиям интегрального признака Коши. Рассмотрим несобственный интеграл
. Эта функция удовлетворяет требованиям интегрального признака Коши. Рассмотрим несобственный интеграл 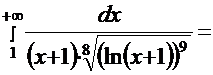


 =
=
|
|
=  число.
число.
Следовательно, несобственный интеграл и ряд из модулей сходятся одновременно по интегральному признаку Коши. Поэтому исходный знакочередующийся ряд сходится абсолютно.
Ответ: сходится абсолютно. 
в)  .
.
Решение. Общий член ряда  .
.
1. Проверим 
 .
.
2. Составим ряд из модулей, 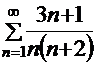 ― знакоположительный ряд, и применим к нему второй признак сравнения. Для сравнения возьмём расходящийся обобщённый гармонический ряд
― знакоположительный ряд, и применим к нему второй признак сравнения. Для сравнения возьмём расходящийся обобщённый гармонический ряд  с общим членом
с общим членом  .
.
Вычислим  . Следовательно, оба ряда расходятся одновременно и абсолютной сходимости исходного знакочередующегося ряда нет.
. Следовательно, оба ряда расходятся одновременно и абсолютной сходимости исходного знакочередующегося ряда нет.
3. Проверим выполнение условий теоремы Лейбница для знакочередующихся рядов:
а)  (это условие проверено в п.1);
(это условие проверено в п.1);
б) Последовательность 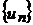 убывает
убывает  .
.
Проверим монотонное убывание с помощью производной: 

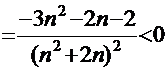 при любых значениях n.
при любых значениях n.
Следовательно, последовательность 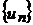 убывает. Оба условия теоремы Лейбница выполняются и исходный знакочередующийся ряд сходится условно.
убывает. Оба условия теоремы Лейбница выполняются и исходный знакочередующийся ряд сходится условно.
Ответ: сходится условно.