Второе начало термодинамики. Энтропия. Циклы.

Министерство образования и науки Российской федерации

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«Ростовский государственный строительный университет»

 

 

Утверждено

на заседании кафедры физики

25 октября 2007 г.

 

 

ИНФОРМАЦИОННО-методическИЕ УКАЗАНИЯ К КОМПЬЮТЕРНОМУ ТЕСТИРОВАНИЮ ПО ФИЗИКЕ. ЧАСТЬ III. МОЛЕКУЛЯРНая ФИЗИКА, ТЕРМОДИНАМИКА

 

 

Ростов-на-Дону

 

 

УДК 531.383

Информационно-методические указания к компьютерному тестированию по физике. Часть III. Молекулярная физика, термодинамика.

– Ростов н/Д: Рост. гос. строит. ун-т, 2008. – 11 с.

 

 

Содержатся тестовые задания для проверки уровня подготовки студентов по курсу физики, а также необходимый теоретический материал для самостоятельной работы студентов при подготовке к защите лабораторных работ физического практикума, к промежуточной и итоговой аттестациям студентов, к сдаче зачетов и экзаменов.

Предназначены для студентов всех специальностей РГСУ, предусматривающих изучение курса физики.

 

Составители: проф. Н.Н.Харабаев,

проф. А.Н.Павлов

Рецензент: доц. Ю.И.Гольцов

 

Редактор Н.Е.Гладких

Темплан 2008 года, поз. 192

Подписано в печать 8.02.08

Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л. 0,7

Тираж 100 экз. Заказ

___________________________________________________________

 

Редакционно-издательский центр

Ростовского государственного строительного университета

334022, Ростов-на-Дону, ул. Социалистическая, 162.

 

 

© Ростовский государственный

строительный университет, 2008

РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА И БОЛЬЦМАНА

 

ЗАДАНИЕ № 1

 

Число молекул в стакане воды примерно равно (молярная масса воды 18 г/моль)...

 

ВАРИАНТЫОТВЕТОВ:

 

1) 10²²; 2) 10²⁰;3) 10²⁶; 4)10²⁸; 5) 10²⁴.

---------------------------

Указание

Число молекул , где N_A – число Авогадро (N_A = 6,02×10²³ моль ^-1).

ЗАДАНИЕ № 2

 

На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где f(v)=(dN/dv)/N – доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.

 

 

Выберите верные утверждения.

 

ВАРИАНТЫОТВЕТОВ:

1. С ростом температуры площадь под кривой растет.

2. С ростом температуры максимум кривой смещается вправо.

3. С ростом температуры величина максимума растет.

4. Площадь заштрихованной полоски равна доле молекул со скоростями в интервале от v до v + dv.

ЗАДАНИЕ № 3

 

Как изменится характер распределения молекул газа по скоростям при уменьшении массы молекул газа при неизменной температуре?

Выберите верные утверждения.

 

ВАРИАНТЫОТВЕТОВ:

1. Площадь под кривой распределения уменьшится.

2. Площадь под кривой распределения не изменится.

3. Максимум функции распределения сместится в сторону меньших скоростей.

4. Максимум функции распределения сместится в сторону больших скоростей.

5. Положение максимума функции распределения не изменится.

---------------------------

Указание к заданиям № 2, 3

Наиболее вероятная скорость движения молекул газа: 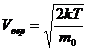(m₀ – масса молекулы газа).

 

ВНУТРЕННЯЯ ЭНЕРГИЯ И ТЕПЛОЕМКОСТЬ ГАЗОВ

ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ

 

ЗАДАНИЕ № 4

Укажите, в какой из приведенных единиц измерения не может быть выражена постоянная Больцмана.

 

ВАРИАНТЫОТВЕТОВ:

1) Дж/К; 2) кгм²/(с²К); 3) кгм²/(сК); 4) Нм/К; 5) эВ/К.

ЗАДАНИЕ № 5

Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. При условии, что имеют место только поступательное и вращательное движения, средняя кинетическая энергия молекул азота (N₂) равна...

 

ВАРИАНТЫОТВЕТОВ:

 

1) kT/ 2; 2) 3 kT/ 2;3)5 kT/ 2; 4) 3 kT;5) 7 kT/ 2.

 

ЗАДАНИЕ № 6

 

В классическом описании газа из N двухатомных молекул используются две возможные модели для молекулы:

1 модель 2 модель

О^______О O-\/\/\/\/-О

Жесткая гантель Упpугая гантель
Какое из следующих утвеpждений веpно для этого газа?

ВАРИАНТЫОТВЕТОВ:

1. Удельная теплоемкость для втоpой модели меньше, чем для пеpвой модели.

2. Модель 1 всегда коppектна.

3. Модель 2 всегда коppектна.

4. Модель 1 имеет теплоемкость C_V= (3/2)^. k^.N_А (k – постоянная Больцмана).

5. Выбоp модели зависит от темпеpатуpы.

---------------------------

Указания к заданиям № 4 – 6

 

Средняя кинетическая энергия молекулы идеального газа при температуре Т равна . Здесь i = п_п + п_вр + 2п_к, где п_п , п_вр и п_к – число степеней

свободы поступательного, вращательного и колебательного движений молекулы.

Молярная теплоемкость при постоянном объеме C_v и при постоянном давлении C_p: ,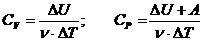

где DU – изменение внутренней энергии; A – работа над внешними телами;

n – число молей; DT – изменение температуры.

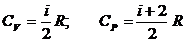(i – число степеней свободы молекулы).

– уравнение Майера. R=kN_A (N_A – число Авогадро).

Для многоатомных молекул число степеней свободы, проявляющихся в теплоемкости газа, зависит от температуры. С повышением температуры, кроме степеней свободы поступательного движения, увеличивается роль степеней свободы вращательного и колебательного движений молекулы.

 

ЗАДАНИЕ № 7

Состояние идеального газа определяется значениями параметров: T₀, p₀, V₀,

где Т – термодинамическая температура, р – давление, V – объем газа. Определенное количество газа перевели из состояния (р₀, V₀) в состояние

(2 р₀, V _o/3). При этом его внутренняя энергия...

 

ВАРИАНТЫОТВЕТОВ:

1) не изменилась; 2) уменьшилась;3) увеличилась.

 

---------------------------

Указания

Уравнение Клапейрона-Менделеева: .

Изменение внутренней энергии идеального газа: .

ЗАДАНИЕ № 8

 

Если DU – изменение внутренней энергии идеального газа, А – работа газа,

Q – количество теплоты, сообщаемое газу, то для адиабатного расширения газа справедливы соотношения...

ВАРИАНТЫОТВЕТОВ:

1) Q> 0; A> 0; DU= 0;

2) Q< 0; A< 0; DU= 0;

3) Q= 0; A< 0; DU> 0;

4) Q= 0; A> 0; DU< 0.

ЗАДАНИЕ № 9

 

Если DU – изменение внутренней энергии идеального газа, А – работа газа,

Q – количество теплоты, сообщаемое газу, то для изотермического сжатия газа справедливы соотношения...

ВАРИАНТЫОТВЕТОВ:

1) Q= 0; A< 0; DU> 0;

2) Q< 0; A> 0; DU= 0;

3) Q> 0; A< 0; DU< 0;

4) Q< 0; A< 0; DU= 0.

 

 

ЗАДАНИЕ № 10

 

Если DU – изменение внутренней энергии идеального газа, А – работа газа,

Q – количество теплоты, сообщаемое газу, то для изобарного расширения газа справедливы соотношения...

ВАРИАНТЫОТВЕТОВ:

1) Q= 0; A> 0; DU< 0;

2) Q> 0; A> 0; DU> 0;

3) Q< 0; A< 0; DU> 0;

4) Q> 0; A> 0; DU= 0.

 

ЗАДАНИЕ № 11

 

Если DU – изменение внутренней энергии идеального газа, А – работа газа,

Q – количество теплоты, сообщаемое газу, то для изохорного нагревания газа справедливы соотношения...

ВАРИАНТЫОТВЕТОВ:

1) Q= 0; A< 0; DU> 0;

2) Q< 0; A= 0; DU> 0;

3) Q> 0; A= 0; DU> 0;

4) Q > 0; A> 0; DU> 0.

 

---------------------------

Указания к заданиям № 8 - 11

 

Уравнение адиабатного (Q= 0) процесса в координатах (V, T): .

Работа при адиабатном процессе: .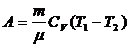

Уравнение изотермического (T=const) процесса: .

Работа при изотермическом процессе: .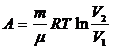

Уравнение изобарного (p=const) процесса: .

Работа при изобарном процессе: .

Уравнение изохорного (V=const) процесса: .

Работа при изохорном процессе: .

Изменение внутренней энергии: .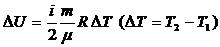

Первое начало термодинамики: .

 

 

ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ЭНТРОПИЯ. ЦИКЛЫ.

 

ЗАДАНИЕ № 12

На (p,V)-диаграмме изображены два циклических процесса. Отношение работ, совершенных в каждом цикле А_I/А_II, равно…

ВАРИАНТЫОТВЕТОВ: 1) 2; 2) -1/2; 3) -2; 4) 1/2.

 

---------------------------

Указания

Работа при круговом процессе: .

Работа А при круговом процессе равна по величине площади, ограниченной замкнутой кривой (контуром) зависимости p(V) на графике кругового процесса в координатах (p, V), а знак (+ или -) определяется направлением обхода по контуру (по часовой стрелке “ + “, против часовой стрелки “ – “).

ЗАДАНИЕ № 13

 

На рисунке 1-2-5 – изотерма, 6-3-4 – изотерма, 2-3, 5-6, 4-1 – адиабаты. Рассматриваются 2 цикла: I – 12341, II – 15641. Какое из соотношений для КПД циклов справедливо?

ВАРИАНТЫОТВЕТОВ: 1) КПД1<КПД2; 2) КПД1>КПД2; 3) КПД1=КПД2.

 

 

ЗАДАНИЕ № 14

Тепловая машина работает по циклу Карно. Если температуру нагревателя увеличить, то КПД цикла...

 

ВАРИАНТЫОТВЕТОВ:

1) не изменится; 2) уменьшится; 3) увеличится.

ЗАДАНИЕ № 15

Тепловая машина работает по циклу Карно. Если температуру холодильника увеличить, то КПД цикла...

 

ВАРИАНТЫОТВЕТОВ:

1) не изменится; 2) уменьшится; 3) увеличится.

 

ЗАДАНИЕ № 16

На рисунке изображен цикл Карно в координатах (T, S), где S-энтропия. Теплота подводится к системе на участке …

 

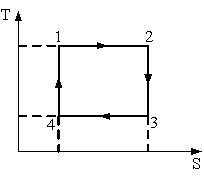
ВАРИАНТЫОТВЕТОВ: 1) 1 – 2; 2) 2 – 3;   3) 3 – 4; 4) 4 – 1.

 

ЗАДАНИЕ № 17

 

На рисунке изображен цикл Карно в координатах (T, S), где S – энтропия. Изотермическое расширение происходит на этапе...

 

ВАРИАНТЫОТВЕТОВ: 1) 1 – 2; 2) 2 – 3;   3) 3 – 4; 4) 4 – 1.

 

ЗАДАНИЕ № 18

 

На рисунке изображен цикл Карно в координатах (T,S), где S – энтропия. Адиабатное сжатие происходит на этапе...

 

ВАРИАНТЫОТВЕТОВ: 1) 1 – 2; 2) 2 – 3;   3) 3 – 4; 4) 4 – 1.

ЗАДАНИЕ № 19

Система совеpшает цикл Каpно, получая количество теплоты Q₁ от нагpевателя пpи темпеpатуpе T₁ и отдавая количество теплоты Q₂ холодильнику пpи темпеpатуpе T₂. Все следующие утвеpждения веpны, за исключением:

ВАРИАНТЫОТВЕТОВ: 1. Энтpопия нагpевателя уменьшается. 2. КПД цикла не зависит от пpиpоды pабочего тела. 3. Выполненная pабота pавна Q1 – Q2. 4. Q1/T1=Q2/T2. 5. Энтpопия системы возpастает.

 

---------------------------

Указания к заданиям № 13 – 19

 

КПД цикла Карно: ,

где Q₁ – количество теплоты, полученное рабочим телом от нагревателя при температуре нагревателя Т₁,

Q₂ – количество теплоты, отданное рабочим телом холодильнику при температуре холодильника Т₂.

Цикл Карно состоит из чередующихся двух изотерм (расширения при температуре нагревателя Т₁ и сжатия при температуре холодильнике Т₂) и двух адиабат (расширения и сжатия).

Второе начало термодинамики: при необратимых процессах энтропия возрастает.

 

 

ЯВЛЕНИЯ ПЕРЕНОСА

ЗАДАНИЕ № 20

 

Явление диффузии имеет место при наличии градиента...

 

ВАРИАНТЫОТВЕТОВ:

1) температуры;

2) электрического заряда;

3) скорости слоев жидкости или газа;

4) концентрации.

 

ЗАДАНИЕ № 21

 

При нагревании тела градиент температуры направлен вдоль оси +ОУ. В каком направлении происходит перенос тепла?

 

ВАРИАНТЫОТВЕТОВ:

1) + OХ; 2) – OZ; 3) – ОУ; 4) + OZ;5) + ОУ.

ЗАДАНИЕ № 22

В жидкости вектор градиента концентрации примеси направлен вдоль оси + ОХ. В каком направлении происходит перенос массы примеси?

 

ВАРИАНТЫОТВЕТОВ:

 

1) + OZ; 2) + OХ; 3) – OZ; 4) + ОУ; 5) – ОХ.

---------------------------

Указания к заданиям № 20 – 22

Закон теплопроводности Фурье: , где Q – теплота, прошедшая посредством теплопроводности через площадь S за время t в направлении х, перпендикулярном площадке S;

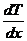– градиент температуры Т вдоль оси х;

l – коэффициент теплопроводности.

Закон диффузии Фика: где m – масса вещества, переносимая посредством диффузии через площадь S за время t в направлении х, перпендикулярном площадке S;

– градиент плотности вещества r вдоль оси х;

D – коэффициент диффузии.