Вырожденное распределение
Говорят, что случайная величина  имеет вырожденное распределение в точке
имеет вырожденное распределение в точке  , и пишут:
, и пишут:  , если
, если  принимает единственное значение
принимает единственное значение  с вероятностью 1, т.е.
с вероятностью 1, т.е.  . Функция распределения
. Функция распределения  имеет вид:
имеет вид:

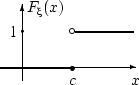
Распределение Бернулли
Говорят, что случайная величина  имеет распределение Бернулли с параметром
имеет распределение Бернулли с параметром 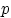 , и пишут:
, и пишут:  , если
, если  принимает значения 1 и 0 с вероятностями
принимает значения 1 и 0 с вероятностями 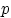 и
и  соответственно. Случайная величина
соответственно. Случайная величина  с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха
с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха 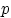 : ни одного успеха или один успех. Таблица распределения
: ни одного успеха или один успех. Таблица распределения  имеет вид:
имеет вид:

| |||||

| 
| 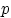
| |||
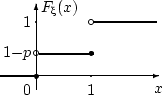
Функция распределения случайной величины  такова:
такова:

Биномиальное распределение
Говорят, что случайная величина  имеет биномиальное распределение с параметрами
имеет биномиальное распределение с параметрами  и
и 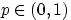 , и пишут:
, и пишут:  , если
, если  принимает значения
принимает значения  с вероятностями
с вероятностями  . Случайная величина с таким распределением имеет смысл числа успехов в
. Случайная величина с таким распределением имеет смысл числа успехов в  испытаниях схемы Бернулли с вероятностью успеха
испытаниях схемы Бернулли с вероятностью успеха 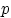 . Таблица распределения
. Таблица распределения  имеет вид:
имеет вид:

Распределение Бернулли совпадает с распределением  .
.
Распределение Пуассона
Говорят, что случайная величина  имеет распределение Пуассона с параметром
имеет распределение Пуассона с параметром  , где
, где  , и пишут:
, и пишут: 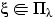 , если
, если  принимает значения
принимает значения  с вероятностями
с вероятностями  .
.
Геометрическое распределение
Говорят, что случайная величина  имеет геометрическое распределение с параметром
имеет геометрическое распределение с параметром 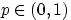 , и пишут
, и пишут  , если
, если  принимает значения
принимает значения  с вероятностями
с вероятностями  . Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха
. Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха 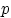 . Таблица распределения
. Таблица распределения  имеет вид:
имеет вид:

Равномерное распределение
Говорят, что  имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке  , и пишут:
, и пишут:  , если плотность распределения
, если плотность распределения  постоянна на отрезке
постоянна на отрезке  и равна нулю вне него:
и равна нулю вне него:


Очевидно, что площадь под графиком этой функции равна единице и  . Поэтому
. Поэтому  является плотностью распределения.
является плотностью распределения.
Случайная величина  имеет смысл координаты точки, выбранной наудачу на отрезке
имеет смысл координаты точки, выбранной наудачу на отрезке  . Вычислим по определению 30 функцию распределения случайной величины
. Вычислим по определению 30 функцию распределения случайной величины  :
:

Получим следующую непрерывную функцию распределения:


Показательное распределение
Говорят, что  имеет показательное (экспоненциальное) распределение с параметром
имеет показательное (экспоненциальное) распределение с параметром  , и пишут:
, и пишут:  , если
, если  имеет следующую плотность распределения:
имеет следующую плотность распределения:


Функция распределения случайной величины  непрерывна:
непрерывна:


Показательное распределение является единственным абсолютно непрерывным распределением, для которого выполнено свойство «нестарения» (и в этом смысле оно является непрерывным аналогом дискретного геометрического распределения).
Гамма-распределение
Говорят, что  имеет гамма-распределение с параметрами
имеет гамма-распределение с параметрами  ,
,  , и пишут:
, и пишут:  , если
, если  имеет следующую плотность распределения:
имеет следующую плотность распределения:

где постоянная  вычисляется из свойства (f2) плотности так:
вычисляется из свойства (f2) плотности так:
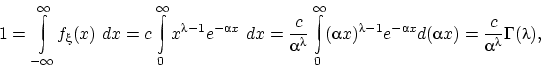
откуда  . Здесь через
. Здесь через  обозначен интеграл
обозначен интеграл

называемый гамма-функцией Эйлера(3);  при целых положительных
при целых положительных  ,
,  . Замена в интеграле Пуассона даст
. Замена в интеграле Пуассона даст  .
.
Показательное распределение — частный случай гамма-распределения:  .
.
Нормальное распределение
Говорят, что  имеет нормальное (гауссовское (1) ) распределение с параметрами
имеет нормальное (гауссовское (1) ) распределение с параметрами 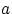 и
и  , где
, где  ,
,  , и пишут:
, и пишут:  , если
, если  имеет следующую плотность распределения:
имеет следующую плотность распределения:


Убедимся, что  является плотностью распределения. Так как
является плотностью распределения. Так как  для всех
для всех  , то свойство (f1) выполнено. Проверим (f2):
, то свойство (f1) выполнено. Проверим (f2):

где через  обозначен табличный интеграл (интеграл Пуассона (2))
обозначен табличный интеграл (интеграл Пуассона (2))

Нормальное распределение  с параметрами
с параметрами  и
и  называется стандартным нормальным распределением. Плотность стандартного нормального распределения равна
называется стандартным нормальным распределением. Плотность стандартного нормального распределения равна  .
.
Ввиду особой роли нормального распределения в теории вероятностей (мы ещё узнаем о ней) существует даже специальное обозначение  для функции распределения нормального закона
для функции распределения нормального закона  . Первообразная функции
. Первообразная функции  не может быть выражена через элементарные функции. Поэтому функцию
не может быть выражена через элементарные функции. Поэтому функцию  можно записать лишь в виде интеграла:
можно записать лишь в виде интеграла:

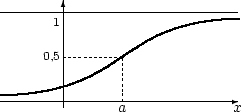
Функция  табулирована, т.е. её значения при различных вещественных
табулирована, т.е. её значения при различных вещественных 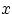 вычислены. Их можно найти в соответствующих таблицах.
вычислены. Их можно найти в соответствующих таблицах.
- Свойства нормального распределения (в том числе вычисление его математического ожидания и дисперсии).
Свойство 1. Для любого  справедливо соотношение:
справедливо соотношение:

Следствие 1. Если  , то
, то  .
.
Следствие 2. Если  , то
, то 
Свойство 2.  ,
, 
Свойство 3. Если  , то для любого
, то для любого 

Свойство 4 (правило трех сигм). Если  , то
, то
 .
.
-------------------------------------------------------------------------------------------------------------------
С тандартное нормальное распределение  :
:
Математическое ожидание этого распределения существует в силу конечности  :
:

Математическое ожидание  равно
равно

так как под сходящимся интегралом стоит нечётная функция. Далее,

Поэтому 
Нормальное распределение  :
:
Если  , то
, то  .
.
 ,
, 

- Определения независимости случайных величин.
Определение 1. Случайные величины  называют независимыми (в совокупности), если для любого набора борелевских множеств
называют независимыми (в совокупности), если для любого набора борелевских множеств  ,...,
,...,  имеет место равенство:
имеет место равенство:

Определение 2. Случайные величины  называют попарно независимыми, если независимы любые две из них.
называют попарно независимыми, если независимы любые две из них.
Определение 3. Случайные величины  независимы (в совокупности), если для любых
независимы (в совокупности), если для любых  имеет место равенство:
имеет место равенство:

Определение 4. Случайные величины  с дискретным распределением независимы (в совокупности), если для любых чисел
с дискретным распределением независимы (в совокупности), если для любых чисел  имеет место равенство:
имеет место равенство:

Определение 5. Случайные величины  с абсолютно непрерывным совместным распределением независимы (в совокупности), если плотность совместного распределения равна произведению плотностей случайных величин
с абсолютно непрерывным совместным распределением независимы (в совокупности), если плотность совместного распределения равна произведению плотностей случайных величин  , т.е. для любых
, т.е. для любых  имеет место равенство:
имеет место равенство:
 .
.
- Определение и свойства математического ожидания.
Определение 1. Математическим ожиданием  (средним значением, первым моментом) случайной величины
(средним значением, первым моментом) случайной величины  с дискретным распределением, задаваемым таблицей
с дискретным распределением, задаваемым таблицей  , где
, где  , называется число
, называется число

если данный ряд абсолютно сходится, т.е. если  . В противном случае говорят, что математическое ожидание не существует.
. В противном случае говорят, что математическое ожидание не существует.
Определение 2. Математическим ожиданием  (средним значением, первым моментом) случайной величины
(средним значением, первым моментом) случайной величины  с абсолютно непрерывным распределением с плотностью распределения
с абсолютно непрерывным распределением с плотностью распределения  называется число
называется число

если этот интеграл абсолютно сходится, т.е. если 
В противном случае математическое ожидание не существует.
-----------------------------------------------------------------------------------------------------------------
Во всех свойствах предполагается, что рассматриваемые математические ожидания существуют.
1.
Для произвольной борелевской функции 

2.
Математическое ожидание постоянной равно ей самой: 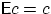 .
.
3.
Постоянную можно вынести за знак математического ожидания: 
4.
Математическое ожидание суммы любых случайных величин равно сумме их математических ожиданий, если только эти математические ожидания существуют:

5.
Если  п.н., т.е. если
п.н., т.е. если  , то
, то  .
.
6.
Если  п.н., и при этом
п.н., и при этом  , то
, то  п.н., т.е.
п.н., т.е.  .
.
7.
Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: если  и
и  независимы и их математические ожидания существуют, то
независимы и их математические ожидания существуют, то

- Определение и свойства дисперсии.
Дисперсия  есть «среднее значение квадрата отклонения случайной величины
есть «среднее значение квадрата отклонения случайной величины  от своего среднего». Посмотрим, за что эта величина отвечает.
от своего среднего». Посмотрим, за что эта величина отвечает.
Пусть случайная величина  принимает значения
принимает значения  с равными вероятностями, а случайная величина
с равными вероятностями, а случайная величина  — значения
— значения  с равными вероятностями. Тогда
с равными вероятностями. Тогда  , поэтому
, поэтому  ,
,  . Говорят, что дисперсия характеризует степень разброса значений случайной величины вокруг её математического ожидания.
. Говорят, что дисперсия характеризует степень разброса значений случайной величины вокруг её математического ожидания.
---------------------------------------------------------------------------------------------------------------------
Свойства дисперсии следуют из соответствующих свойств математического ожидания.
1.
Дисперсия может быть вычислена по формуле:  .
.
2.
При умножении случайной величины на постоянную  дисперсия увеличивается в
дисперсия увеличивается в  раз:
раз:  .
.
3.
— Дисперсия всегда неотрицательна:  .
.
— Дисперсия обращается в нуль лишь для вырожденного распределения: если  , то
, то  п. н., и наоборот.
п. н., и наоборот.
4.
Дисперсия не зависит от сдвига случайной величины на постоянную:  .
.
5.
Если  и
и  независимы, то дисперсия их суммы равна сумме их дисперсий:
независимы, то дисперсия их суммы равна сумме их дисперсий:  .
.
6.
Минимум среднеквадратического отклонения случайной величины  от точек вещественной прямой есть среднеквадратическое отклонение
от точек вещественной прямой есть среднеквадратическое отклонение  от своего математического ожидания:
от своего математического ожидания:  .
.
- Определение и свойства коэффициента корреляции.
Коэффициентом корреляции  случайных величин
случайных величин  и
и  , дисперсии которых существуют и отличны от нуля, называется число
, дисперсии которых существуют и отличны от нуля, называется число

-----------------------------------------------------------------------------------------------------------------
Коэффициент корреляции обладает свойствами:
1)
если  и
и  независимы, то
независимы, то  ;
;
2)
всегда  ;
;
3)
 тогда и только тогда, когда
тогда и только тогда, когда  и
и  п. н. линейно связаны, т.е. существуют числа
п. н. линейно связаны, т.е. существуют числа  и
и  такие, что
такие, что  .
.
[Сокращение «п.н.» читается как «почти наверное» и означает «с вероятностью 1»]
- Определение сходимости по вероятности. Неравенства Маркова и Чебышёва.
Говорят, что последовательность случайных величин 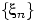 сходится по вероятности к случайной величине
сходится по вероятности к случайной величине  при
при  , и пишут:
, и пишут:  , если для любого
, если для любого 

------------------------------------------------------------------------------------------------------------------
(неравенство Маркова). Если  , то для любого
, то для любого 
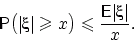
(обобщённое неравенство Чебышёва). Пусть функция  не убывает и неотрицательна на
не убывает и неотрицательна на 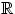 . Если
. Если  , то для любого
, то для любого 

- Закон больших чисел в форме Чебышёва (с док-вом). Закон больших чисел Бернулли.
Для любой последовательности  попарно независимых и одинаково распределённых случайных величин с конечным вторым моментом
попарно независимых и одинаково распределённых случайных величин с конечным вторым моментом  имеет место сходимость:
имеет место сходимость:

Доказательство.
Обозначим через  сумму первых
сумму первых  случайных величин. Из линейности математического ожидания получим:
случайных величин. Из линейности математического ожидания получим:

Пусть  . Воспользуемся неравенством Чебышёва:
. Воспользуемся неравенством Чебышёва:

|
так как  . Заметим, что дисперсия суммы превратилась в сумму дисперсий в силу попарной независимости слагаемых, из-за которой все ковариации
. Заметим, что дисперсия суммы превратилась в сумму дисперсий в силу попарной независимости слагаемых, из-за которой все ковариации  обратились в нуль при
обратились в нуль при  . Сумма же дисперсий слагаемых равняется
. Сумма же дисперсий слагаемых равняется  из-за их одинаковой распределённости.
из-за их одинаковой распределённости.
-------------------------------------------------------------------------------------------------------------------
Пусть событие  может произойти в любом из
может произойти в любом из  независимых испытаний с одной и той же вероятностью
независимых испытаний с одной и той же вероятностью 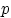 , и пусть
, и пусть  — число осуществлений события
— число осуществлений события  в
в  испытаниях. Тогда
испытаниях. Тогда  . При этом для любого
. При этом для любого 
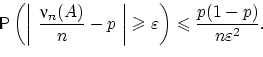
- Определение сходимости по распределению (слабой сходимости).
Пусть задана последовательность случайных величин  , задано некоторое распределение
, задано некоторое распределение 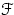 с функцией распределения
с функцией распределения  и пусть
и пусть  — произвольная случайная величина, имеющая распределение
— произвольная случайная величина, имеющая распределение 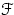 .
.
Говорят, что последовательность случайных величин  сходится слабо или по распределению к случайной величине
сходится слабо или по распределению к случайной величине  и пишут:
и пишут:  , если для любого
, если для любого 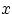 такого, что функция распределения
такого, что функция распределения  непрерывна в точке
непрерывна в точке 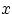 , имеет место сходимость
, имеет место сходимость
 при
при  .
.
Итак, слабая сходимость — это сходимость функций распределения во всех точках непрерывности предельной функции распределения.
- Центральная предельная теорема.
(ЦПТ Ляпунова). Пусть  — независимые и одинаково распределённые случайные величины с конечной и ненулевой дисперсией:
— независимые и одинаково распределённые случайные величины с конечной и ненулевой дисперсией:  . Тогда имеет место слабая сходимость
. Тогда имеет место слабая сходимость

последовательности «центрированных и нормированных» сумм случайных величин к стандартному нормальному распределению.