ИЗОБРАЖЕНИЕ ТОЧКИ, ОБРАЗУЕМОЕ СФЕРИЧЕСКОЙ ПРЕЛОМЛЯЮЩЕЙ ПОВЕРХНОСТЬЮ.

СВОЙСТВА ОПТИЧЕСКИХ СИСТЕМ В ПАРАКСИАЛЬНОЙ ОБЛАСТИ.

ОПТИЧЕСКАЯ СИСТЕМА СО СФЕРИЧЕСКИМИ ПОВЕРХНОСТЯМИ.

(т.1 с.13)

Основными оптическими деталями, входящими в оптическую систему, являются линзы и зеркала со сферическими поверхностями. Плоская поверхность рассматривается как сфера с радиусом кривизны, равным бесконечности. Детали располагаются таким образом, что все центры кривизны отдельных поверхностей (О1 - О4) лежат на одной линии АА', называемой оптической осью системы (рис. 1.1),а сама система называется центрированной.

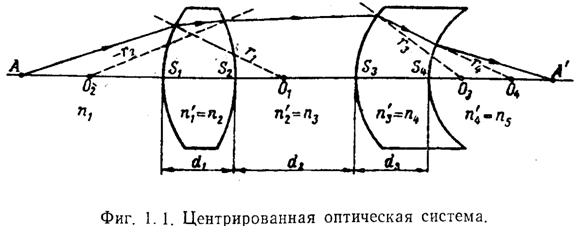
Очевидно, оптическая ось является осью круговой симметрии. Плоскость, проходящая через оптическую ось системы, называется меридиональной.

Если входящий в оптическую систему луч лежит в меридиональной плоскости, то в следствие центрированности системы и закона преломления этот луч при прохождении через оптическую систему остается в этой плоскости.

Конструктивные параметры системы - радиусы кривизны, расстояния между оптическими поверхностями вдоль оптической оси и показатели преломления сред.

Свет распространяется слева на право, а точки пересечения преломляющих поверхностей с оптической осью S1,S2... называются вершинами этих поверхностей.

Радиус кривизны отсчитывается от вершины поверхности и считается положительным, если центр кривизны расположен от поверхности по направлению луча (вправо), в противоположном случае радиус кривизны будет отрицательным. (рис.1.2)

ИЗОБРАЖЕНИЕ ТОЧКИ, ОБРАЗУЕМОЕ СФЕРИЧЕСКОЙ ПРЕЛОМЛЯЮЩЕЙ ПОВЕРХНОСТЬЮ.

(т.1 с.14)

Пусть сферическая поверхность разграничивает две среды с показателями преломления n и n' (рис 1.3).

Возьмем на оптической оси светящуюся точку А. Расстояние от вершины поверхности S до этой точки обозначим через s. Если точка А расположена от вершины влево, то расстояние s будет отрицательным (s < 0), если точка А расположена от вершины поверхности вправо, то расстояние будет положительным (s > 0). Проведем из точки А произвольный луч, который, преломляясь, пересечет оптическую ось в точке А' на расстоянии s' от вершины поверхности. Для отрезка s' правила знаков те же, как и для отрезка s. Углы входного луча АМ с оптической осью и нормалью к поверхности будем обозначать через u и i, а для преломленного луча соответственно через u' и i'.

Условимся отсчитывать углы от какой-нибудь определенной оси, точно указываемой в каждом отдельном случае; будем считать угол положительным, если этот угол можно образовать вращением прямой линии от указанной оси по часовой стрелке, и отрицательным против часовой стрелки.

За начальные оси будем считать:

для отсчета углов u и u' - оптическую ось, а для отсчета углов i и i' - нормаль к поверхности в точке падения луча.

В соответствии с этим на рис.1.3 u < 0, u' > 0 и i < 0, i' < 0.

С учетом закона преломления находим следующий ряд зависимостей:

- из треугольника АМО следует

(1.1)

Пользуясь законом преломления, получим

(1.2)

- из треугольника А'МО будем иметь

u' = -i+i'+u, (1.3)

(1.4)

(1.5)

Последовательное применение формул (1.1), (1.2), (1.3),(1.4),(1.5) дает возможность при заданных значениях r, n, n' и s вычислить величину отрезка s', определяющего положение точки А'.

Пучок лучей после преломления перестает быть гомоцентричным и поэтому изображение точки отсутствует.

В общем случае ход лучей изображен на рис.1.7.

Нарушение гомоцентричности в пучке преломленных или отраженных лучей вызывает ошибки изображения, которые называются аберрациями.

Если углы лучей с оптической осью и нормалями к поверхности настолько малы, что значения синусов этих углов можно заменить значениями самих углов, выраженных в радианах, то такие лучи называются параксиальными или нулевыми лучами, а область вокруг оптической оси, внутри которой распространяются эти лучи, называется параксиальной областью.

Рассмотрим в параксильной области изображение малого отрезка dl перпендикулярного к оптической оси в точке А (рис.1.8). Пусть dl' будет изображением этого отрезка. Если отрезки dl и dl' направлены от оси системе вверх, то они считаются положительными, а если вниз - отрицательными. Отношение величины изображения к величине предмета:

(1.10)

назывется линейным, или поперечным увеличением. При b >0 изображение называется прямым, при b < 0 изображение будет обратным..

Обозначим вершину отрезка dl через С и изображение ее через С'. Проведем из точки С два луча: луч СО через центр поверхности (точку О) - этот луч пройдет через поверхность не преломляясь, а второй луч – СS через вершину поверхности S. Рассматривая подобные треугольники, образованные первым лучом, и используя закон преломления для второго луча, получим:

(1.9)

(1.11)

Полученные зависимости (1.9) и (1.11) позволяют сделать выводы, а именно: каждому положению предметной точки соответствует вполне определенное положение ее изображения, и каждому малому отрезку, перпендикулярного к оптической оси, соответствует изображение так же отрезка, перпендикулярного к оптической оси. Такие пары точек и отрезков называются сопряженными.

Т.к. два пересекающихся отрезка, перпендикулярных к оптической оси, определяют плоскость, то, следовательно, элемент плоскости ds', перпендикулярный к оптической оси, изображается также элементом плоскости ds', перпендикулярным к этой же оси (рис 1.9)

Отсюда так же следует, что всякий гомоцентричный пучок после преломления в параксильной области имеет свою, ему одному соответствующую точку схода.

Из формулы (1.11) получается:

(1.12)

известная под названием теоремы Гюйгенса-Гельмгольца.

В литературе эта формула встречается так же под название Лагранжа-Гельмгольца.

§1.3 ИЗОБРАЖЕНИЕ В ОПТИЧЕСКОЙ СИСТЕМЕ, СОСТОЯЩЕЙ ИЗ РЯДА СФЕРИЧЕСКИХ ПОВЕРХНОСТЕЙ.

(т.1 с.19)

Рассмотрим образование изображений в параксильной области оптической системы, состоящей из ряда сферических поверхностей 1, 2,... к,...р. (рис 1.10).

Т.к. изображение любой предметной точки является в свою очередь предметом для последующей поверхности, то исходя из фигуры можно записать:

, … .

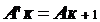Кроме того:

, …

и т. д. Из формулы (1.12), применяя ее к каждой из преломляющих поверхностей, получим

(1.13)

Формула (1.13) дает возможность определить линейное увеличение для всей системы:

(1.14)

Для определения положения и величины изображения рассмотрим два способа:

1 способ основан на расчете хода луча, вышедшего из предметной точки через оптическую систему. Для вывода расчетных формул воспользуемся рис 1.10 и формулой (1.9).Умножим обе части формулы (1.9) на величину h,обозначающую высоту пересечения луча с поверхностью:

Производя замену:

;

окончательно получим

(1.15)

Из рис 1.10 также следует (для параксиальной области)

(1.16)

Зная для выбранного луча входные координаты u и h, причем

и применяя последовательно к каждой из поверхностей формулы (1.15) и (1.16), найдем все значения углов и высот:

u = u = u = … u'=

h = h = h = … h =

Таким образом, положение изображения s', линейное увеличение и величина изображения dl' определяется по формулам

(1.17)

(1.18)

(1.19)

2 способ - последовательное применение формулы (1.9)к каждой из поверхностей (на рис 1.10).

Применительно к поверхности k эта формула примет вид:

(1.20)

и .

В результате этих расчетов мы найдем значения всех отрезков, определяющих положения промежуточных изображений, т.е. будут известны отрезки

Линейное увеличение в этом случае лучше рассматривать как произведение линейных увеличений отдельных поверхностей; принимая во внимание формулу (1.11), получим:

(1.21)