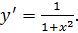Лекция №3.
Тема: Дифференциальное исчисление функции одной переменной.
Основные определения.
Опр. 1. Дифференцированием функции называется операция нахождения производной от функции.
Опр. 2. Производной функции y=f(x) по аргументу x называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю произвольным образом.
f ’(x)=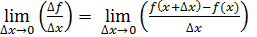 
Замечание: В школе считалось, что производная существует, если этот предел конечен, однако, если lim=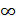 
, то функция f(x) имеет в точке x бесконечную производную.
Геометрический смысл:
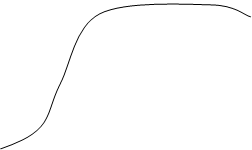
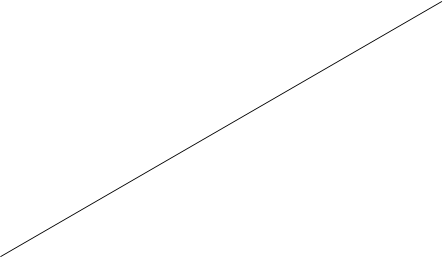Значение производной f ’(x) при заданном значении аргумента x равно тангенсу угла, образованного с положительным направлении оси Ox касательной к графику функции f(x) в точке M0(x0,y0).
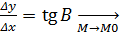tg 
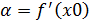
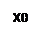
y
 |
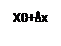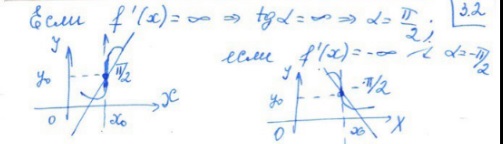
Механический смысл:
Если зависимость расстояния S движущейся точки от времени t выражается формулой S=f(t), то мгновенная (не путать со средней) скорость в момент времени t выражается формулой:
v=S’(t)=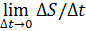 
= 
,
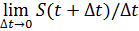т.е. скорость равна производной по пути от времени.
Замечание: Экономический смысл производной будет рассмотрен в отдельном параграфе.
Односторонние производные.
Опр. 1: Односторонней производной функции f(x) по аргументу x называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю слева (левосторонняя) или справа (правосторонняя), т.е.
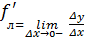
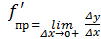
Замечания:
1) Если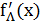 
= 
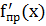, то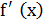 
существует. В противном случае 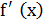не существует.
Пример: y=|x-1|
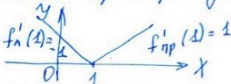
x=1 называется угловой точкой.
2) Рассмотрим случаи бесконечных односторонних производных
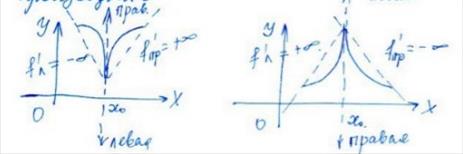
Таблица производных.
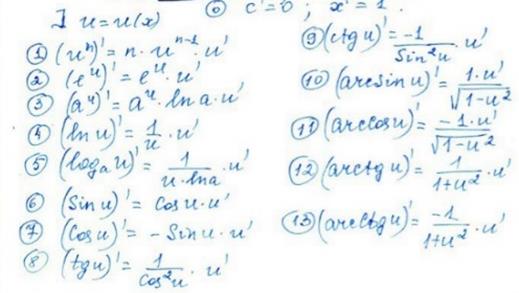
Пример: Вычислить производную функции f(x)=1/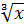 
– lnx*cosx+tgx/x^7 +5sinx*5.
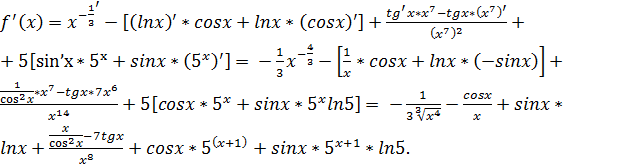
Связь между дифференцируемостью и непрерывностью.
Теорема: Если функция f(x) дифференцируема в (.) x0, то она в этой точке непрерывна.
Док-во:
Если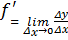 
, тогда по теореме о пределе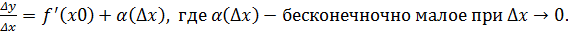 
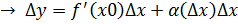
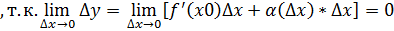
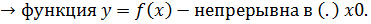
Производная сложной функции.
Теорема: Пусть дана функция y=f(x) такая, что её можно представить в виде y=F(u), u =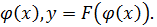 
Тогда, если y=F(u) и u= 
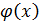имеют производные в некоторые точки u т (.) x, то функция 
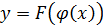имеет в (.) x производную, которая равна
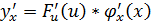
Или кратко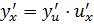 
.
То есть производная сложной функции равна произведению производной данной функции по промежуточному аргументу «и» на производную промежуточного аргумента по x.
Доказательство:
Зададим аргументу x приращение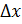 
, тогда функция получит приращение 
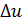и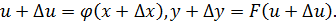 
Таким образом, приращению 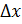соответствует приращение 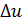, которое соответствует приращению 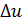, которое соответствует приращению 
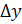, причём при 
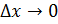будет 
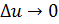и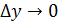 
.
По условию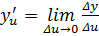 
по определению предела 
= 
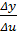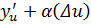, где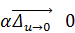 
.
.
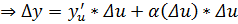Разделим все члены равенства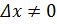 
.
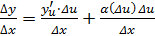, и
 |
 |
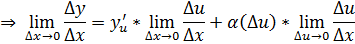
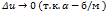
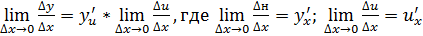- по определению производной.
Отсюда
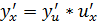ч.т.д.
Пример: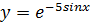 
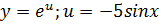
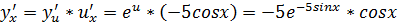
Производная обратной функции.
Пусть задана функция y=f(x), тогда обратная её функция будет иметь вид x=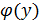 
.
Замечания:
1. Возрастающая или убывающая функции имеют одну обратную функцию.
2. Если возрастающая или убывающая функция y=f(x) непрерывна на [a;b], причём f(a)=c; f(b)=d, тогда обратная функция будет определена и непрерывна на [c;d].
Пример:
y=sinx, x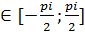 
x=arcsiny, y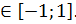 
3. Если функция не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций.
4. Графики обратных функций будут симметричны относительно биссектрисы координат угла или совпадать.
Теорема: Если для функции y=f(x) существует обратная функция x=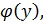 
которая в рассматриваемой точке имеет производную 
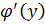, отличную от нуля, то в этой точке функция y=f(x) имеет производную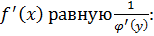 
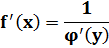
Доказательство: I способ
Пусть аргумент y имеет приращение 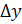, тогда функция x получит приращение
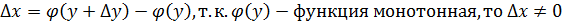
Напишем тождество:
(1) 
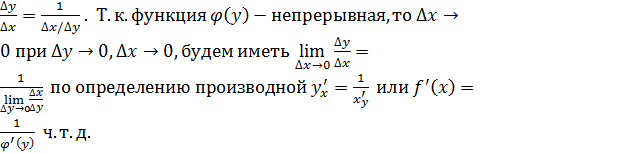
II способ
Т.к. x=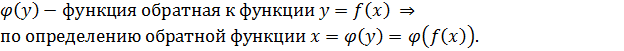 
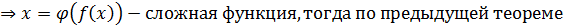
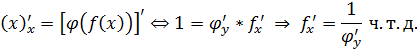
Пример: 1) Пусть y=arcsinx. Докажем, что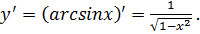 
3) y=arctgx; 