Для решения уравнений с модулями необходимо знать 4 случая:
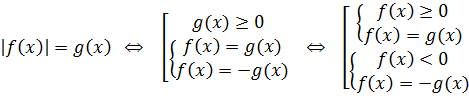
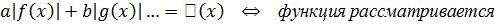
Пример 1:
Решить относительно всех значений параметра a уравнение 
Данное уравнение равносильно совокупности
Оба уравнения являются линейными, поэтому решим их отдельно:
1) 
Если 
, то есть 
уравнение не имеет решений, так как 
, что невозможно, но уравнение 
имеет корень 
;
· Если 
, то есть 
, то 
.
2)
· Если 
, то есть 
уравнение не имеет решений, так как , что невозможно, но уравнение 
имеет корень ;
· Если 
, то есть 
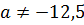, то 
.
Ответ: при 
корень ;
при 
.
Пример 2:
Решить относительно всех значениях параметра a уравнение 
Данное уравнение равносильно совокупности:
Решим каждое уравнение системы отдельно:
1) 
корень 
при a ∊ R;
2) 
· Если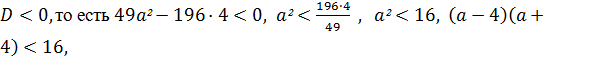 
то есть, если 
, то уравнение не имеет корней;
· Если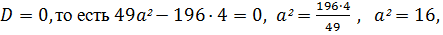 
то есть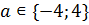, если 
, 
, т.о. если 
;
· Если 
то есть, если 
, то уравнение имеет два различных корня: 
.
3) 
· Если 
, что невозможно, поэтому уравнение не имеет корней;
· Если 
;
· Если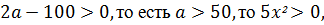 
уравнение имеет два корня: 
.
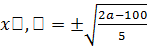Ответ: при 
;
при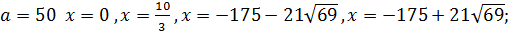 
при 
;
при 
;
при 
, 
, 
;
при 
, 
, , 
.
Пример 3:
Решить относительно параметра a уравнение: 
Данное уравнение равносильно следующей совокупности:
.
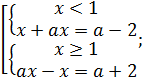
Далее проще рассматривать каждую систему отдельно:
1) 
;
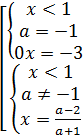Первая система в совокупности решений не имеет, поэтому остается вторая, которую можно преобразовать:
;
2) 
;
Первая система в совокупности решений не имеет, поэтому остается вторая, которую можно преобразовать:
;
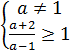Таким образом, исходное уравнение при 
корней не имеет, при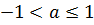 
будет иметь ровно один корень, равный 
, при 
более одного корня.
Ответ: при нет корней,
при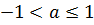 
,
при более одного корня.
Пример 4:
Решить при всех a уравнение 
и определить, при каких значениях параметра a оно имеет ровно два решения.
Данное уравнение равносильно следующей совокупности:
;
;
1) Рассмотрим первую систему. Если a=1, то эта система решений не имеет, если a≠1, то уравнение имеет только одно решение 
. Выясним, при каких a данное x будет удовлетворять первому неравенству системы:
.
Значит, при этих значениях a первая система будет иметь решение , а при остальных значениях a эта системы решений иметь не будет.
2) Теперь рассмотрим вторую систему:
При 
решением уравнения будет любое число x, поэтому при данном значении параметра решением системы будут все x из интервала 
. При 
уравнение будет иметь единственное решение 
, которое является также решением этой системы.
3) В третьей системе при 
решением уравнения будет любое x, поэтому при данном a решением системы будут все 
. При 
уравнение будет иметь единственное решение , котрое не является решением этой системы, поэтому сама система решений иметь не будет.
Рассмотрим, какие решения имеет исходная совокупность при различных значениях параметра a. При первая система совокупность решений не имеет, вторая система имеет решение , третья 
. Поэтому совокупность будет иметь решение x∊[1;+∞). При первая система будет иметь решение 
, вторая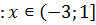 
, третья система сосвокупности решений не имеет. Значит, решением совокупность будет отрезок x∊[-3;1]. При 
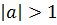первая и третья система решений не имеют, значит, решением совокупность будет решение второй системы . При 
первая система имеет решение , вторая 
, третья система решений не имеет. Значит, решение совокупности будет состоять из двух чисел: 
.
Ответ: если , то x∊[1;+∞);
если , то x∊[-3;1];
если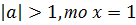 
;
если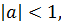 
то и .
При имеются ровно два решения.
Задания для тренировки:
1. Найдите все значения параметра a, при каждом из которых уравнение 
имеет минимум один корень, и укажите число корней уравнения для каждого значения a.
2. Найдите все значения параметра a, при каждом из которых уравнение 
имеет минимум один корень, и укажите корни уравнения для каждого значения a.
3. Решить относительно параметра a уравнение: 
.
4. Найдите все значения параметра a, при каждом из которых уравнение 
имеет единственное решение.
5. Решить относительно параметра a уравнение: 
.