В работе [2] приведены основные реологические модели, характеризующие поведение материалов в зоне контакта. Рост ФПК и силы трения в зависимости от времени неподвижного контакта объясняет схема И.В. Крагельского и А.Ю. Ишлинского, приведенная на рис. 1.7,ж.
Зависимость коэффициента трения от скорости скольжения V в виде экспоненциальной функции предложили И.В. Крагельский и В.С. Щедров:
. (1.49)
Параметры а, в, с, d характеризуют режим скольжения и свойства материалов пары трения. Параметр а зависит от физических свойств материалов и шероховатости, в и с зависят от вязкости и нагрузки, d зависит от конструкции узла трения и режима скольжения. Однако влияние скорости на свойства контакта при небольшом ее изменении само по себе невелико.
Но существенный рост скорости приводит к значительному повышению температуры контакта, поскольку мощность трения (F×V) превращается в теплоту. Рост температуры в свою очередь вызывает заметное изменение свойств материалов в зоне контакта, резко снижается твердость. Поскольку увеличивается ФПК, снижается интенсивность молекулярного взаимодействия (t0, b), происходят химические превращения в поверхностных слоях. При очень больших скоростях скольжения возможно оплавление поверхности, и сухое трение переходит в гидродинамическое. В общем случае наблюдается снижение коэффициента трения с ростом температуры.
Теория тепловых процессов, протекающих при трении, в России наиболее полно разработана профессором А.В. Чичинадзе и его научной школой. В соответствии с этой теорией максимальную температуру на пятне контакта можно представить в виде суммы:
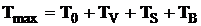, (1.50)
где T0 - исходная температура пары трения, Tv - средняя объемная температура элемента пары, TS - средняя температура на номинальной (контурной) площади контакта, TB - температурная вспышка на пятне контакта. Эти факторы опосредованы теплопроводностью пары трения.
|
|
Задачу теплопроводности обычно формулируют в следующем виде: найти распределение температур в элементах пары трения, когда на контакте действует переменный по времени и положению источник теплоты, а со свободных поверхностей происходит теплоотдача в окружающую среду. При этом учитывают изменение теплофизических характеристик материалов в зависимости от температуры. Решение задачи позволяет рассчитать TV, TS, TB в условиях работы тормозов, сцепления и других узлов трения. Расчеты и эксперименты показали, что Tmax может, даже при сравнительно небольших скоростях, достигать сотен градусов, что приводит к заметным изменениям свойств материалов в тонком поверхностном слое.
При работе разных механизмов часто возникают колебания, связанные с трением. Они приводят к появлению скрипов, которые проявляются при движении (скрип колес, тормозов, скрип протекторов автомобилей, когда машина идет юзом и др.). Такие колебания называют фрикционными. Причинами колебаний являются реологические свойства контакта, а также упругие свойства элементов пары трения и их связей с другими деталями. Главным проявлением реологии контакта является рост ФПК, а следовательно, и статической силы трения с увеличением времени неподвижного контакта и скачкообразное падение силы трения при переходе от покоя к движению, а затем падение силы трения с ростом скорости скольжения, вызванное, главным образом, скачком температуры на пятнах контакта. Динамическая модель такой системы изображена на рис. 1.17.
|
|
Модель представляет собой последовательно соединенные тела Кельвина-Фойгта и Сен-Венана. Если в целях упрощения принять, что h=0, m=const, то 2-й закон Ньютона для колебаний ползуна запишется в виде:
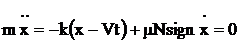. (1.51)
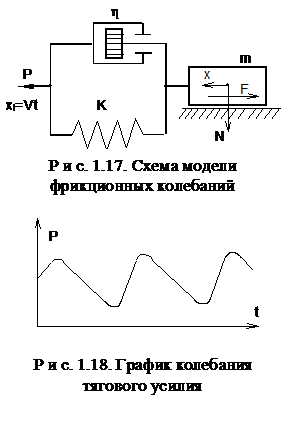Решение этого уравнения позволяет найти законы движения ползуна и колебаний тягового усилия. На рис. 1.18 показан примерный график колебаний тягового усилия. Наиболее обстоятельные теоретические решения в этой области выполнены в МГТУ им. Баумана Ф.Р. Геккером и его учениками.
В зависимости от уровня гашения (вязкости системы m) колебания могут существовать либо не возникать. От этого зависит устойчивость, надежность и долговечность механических систем, что необходимо учитывать при проектировании механизмов и замене деталей при ремонте и техобслуживании.
Трение качения
Если бы колесо, катящееся по основанию, не испытывало проскальзывания, то такое движение было бы чистым качением и путь, проходимый любой точкой поверхности колеса по основанию за один оборот, составлял бы 2pr. Однако качения без проскальзывания не бывает. Колесо и основание испытывают упругие деформации. При этом колесо в зоне контакта сжимается, а основание - растягивается (стрелки на рис. 1.19,а).
а б
Р и с. 1.19. Взаимодействия колеса с опорой
Поэтому на контакте постоянно происходит проскальзывание колеса относительно основания. Это один из источников рассеяния энергии. Другим источником является вязкоупругое поведение материалов основания колеса. Если к оси колеса не приложено тяговое усилие, то дуга контакта симметрична (см. рис. 1.19,а), и реакция опоры соосна с нормальной нагрузкой. Если приложить тяговое усилие и колесо приходит в движение, то зона контакта искажается (см. рис. 1.19,б). Материал сзади колеса не успевает восстановить форму. Эпюра давлений смещается в сторону движения. Большая часть дуги контакта оказывается во фронтальной части. Реакция опоры распределяется на 2 составляющих: вертикальную (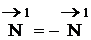
) и горизонтальную (Fl) которая представляет собой сопротивление перекатыванию.
|
|
Поскольку из условия равновесия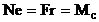 
, то коэффициент трения качения
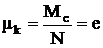, (1.52)
где e - эксцентриситет - смещение центра опорной поверхности от вертикали (см. рис. 1.19,б). Наряду с этой характеристикой используется коэффициент сопротивления качению, равный отношению работы на единичном пути к нормальной нагрузке. Работа при повороте на угол dj равна Mdj, а пройденный путь - Dl = rdj. Тогда коэффициент сопротивления
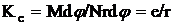. (1.53)
Это выражение было получено Кулоном. Дальнейшие исследования показали, что эксцентриситет не является константой и 
~1/rn, причем n<1.
Далее было установлено, что проскальзывание вносит незначительный вклад в потери энергии, а главный источник потерь - вязкоупругие деформации катка и опоры. Рассеивание энергии связано в основном с гистерезисом деформации. Исходя их этих соображений, для цилиндрического катка
mk =0,24ar (q×r×j)1/2, (1.54)
где q - нагрузка, приходящаяся на единицу длины. Более детально задача о качении жесткого цилиндра по вязкоупругому полупространству решена академиком А.Ю. Ишлинским. Свойства полупространства описаны реологической моделью Кельвина-Фойгта (см. рис. 1.7,г). Для малых скоростей качения
mk=C1V, (1.55)
а для больших скоростей
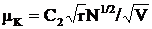. (1.56)
При малых скоростях коэффициент трения качения увеличивается с повышением скорости, а при больших - уменьшается.
Дальнейшее развитие теория трения качения получила в работах И.Г. Горячевой, которая рассмотрела качение вязкоупругих тел при наличии на площадке контакта зон сцепления и проскальзывания. Она показала, что в случае одинаковых материалов зона сцепления располагается на фронтальной части дуги контакта, а проскальзывание - на тыльной.