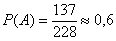теорема умножения вероятностей зависимых событий

- вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло:

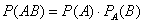
В нашем случае:
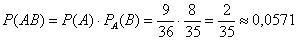– вероятность того, что из полной колоды будут извлечены 2 червы подряд.

Аналогично:
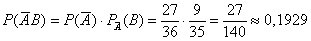– вероятность того, что сначала будет извлечена карта другой масти и затем черва.

Вероятность события 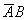получилась заметно больше вероятности события 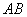, что, в общем-то, было очевидно безо всяких вычислений.

И, само собой, не нужно питать особых надежд, что из конверта с десятью лотерейными билетами (Задача 2) вы вытяните 3 выигрышных билета подряд:

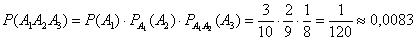
Да, совершенно верно – теорема умножения вероятностей зависимых событий естественным образом распространяется и на бОльшее их количество.

Закрепим материал несколькими типовыми примерами:

Задача 3

В урне 4 белых и 7 черных шаров. Из урны наудачу один за другим извлекают два шара, не возвращая их обратно. Найти вероятность того, что:

а) оба шара будут белыми;
б) оба шара будут чёрными;
в) сначала будет извлечён белый шар, а затем – чёрный.

Обратите внимание на уточнение «не возвращая их обратно». Этот комментарий дополнительно подчёркивает тот факт, что события зависимы. Действительно, а вдруг извлечённые шары возвращают обратно? В случае возвратной выборки вероятности извлечения чёрного и белого шара меняться не будут, а в такой задаче уже следует руководствоваться теоремой умножения вероятностей НЕзависимых событий.

Решение: всего в урне: 4 + 7 = 11 шаров. Поехали:

а) Рассмотрим события 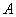– первый шар будет белым, 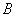– второй шар будет белым и найдём вероятность события 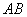, состоящего в том, что 1-й шар будет белым и 2-й белым.

По классическому определению вероятности: 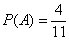. Предположим, что белый шар извлечён, тогда в урне останется 10 шаров, среди которых 3 белых, поэтому:
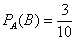– вероятность извлечения белого шара во 2-м испытании при условии, что до этого был извлечён белый шар.

По теореме умножения вероятностей зависимых событий:
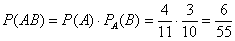– вероятность того, что оба шара будут белыми.

б) Найдём вероятность события 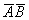, состоящего в том, что 1-й шар будет чёрным и 2-й чёрным

По классическому определению: 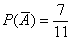– вероятность того, что в 1-м испытании будет извлечён чёрный шар. Пусть извлечён чёрный шар, тогда в урне останется 10 шаров, среди которых 6 чёрных, следовательно: 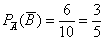– вероятность того, что во 2-м испытании будет извлечён чёрный шар при условии, что до этого был извлечен чёрный шар.

По теореме умножения вероятностей зависимых событий:
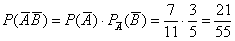– вероятность того, что оба шара будут чёрными.

в) Найдём вероятность события 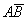(сначала будет извлечён белый шар и затем чёрный)

После извлечения белого шара (с вероятностью 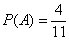) в урне останется 10 шаров, среди которых 3 белых и 7 чёрных, таким образом: 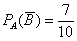– вероятность того, что во 2-м испытании будет извлечён чёрный шар при условии, что до этого был извлечен белый шар.

По теореме умножения вероятностей зависимых событий:
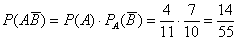– искомая вероятность.

Ответ: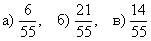

Данную задачу нетрудно проверить через теорему сложения вероятностей событий, образующих полную группу. Для этого найдём вероятность 4-го недостающего события: 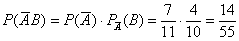– того, что сначала будет извлечён чёрный шар и затем белый.

События 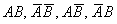образуют полную группу, поэтому сумма их вероятностей должна равняться единице:
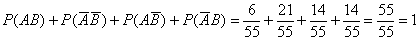,что и требовалось проверить.

Задача 4

Какова вероятность того, что из колоды в 36 карт будут извлечены два туза подряд?

Решение: всего: 4 туза в колоде. Рассмотрим события 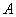– первой картой будет извлечён туз, 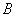– 2-й картой будет извлечён туз. По классическому определению вероятности: 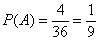. В случае осуществления события 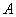в колоде останется 35 карт, среди которых 3 туза, поэтому: 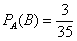– вероятность того, что 2-й картой будет извлечён туз, при условии, что до этого был извлечен туз.
По теореме умножения вероятностей зависимых событий:
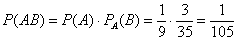– вероятность того, что из колоды в 36 карт будут извлечены два туза подряд.
Ответ: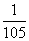

Задача 5

В урне 6 черных, 5 красных и 4 белых шара. Последовательно извлекают три шара. Найти вероятность того, что

а) третий шар окажется белым, если до этого был извлечён черный и красный шар;
б) первый шар окажется черным, второй – красным и третий – белым.

Решение: всего: 6 + 5 + 4 = 15 шаров в урне. Рассмотрим следующие события:
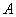– 1-й шар будет черным;
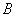– 2-й шар будет красным;
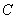– 3-й шар будет белым.

а) По условию, события 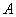и 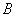уже произошли, а значит, в урне осталось 13 шаров, среди которых 4 белых. По классическому определению: 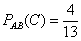– вероятность того, что 3-й шар будет белым при условии, что до этого был извлечён черный и красный шар.

б) По классическому определению: 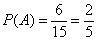. Предположим, что событие 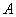произошло, тогда в урне осталось 14 шаров, среди которых 5 красных. По классическому определению: 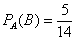– вероятность того, что 2-й шар будет красным при условии, что 1-й был чёрным.
По теореме умножения вероятностей зависимых событий:
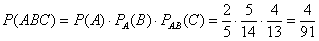– вероятность того, что первый шар окажется черным и второй – красным и третий – белым

Ответ: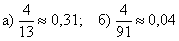

Надо сказать, что многие из рассматриваемых задач разрешимы и другим способом, но чтобы не возникло путаницы, пожалуй, вообще о нём умолчу.

Наверное, все заметили, что зависимые события возникают в тех случаях, когда осуществляется некоторая цепочка действий. Однако сама по себе последовательность действий ещё не гарантируют зависимость событий. Пусть, например, студент наугад отвечает на вопросы какого-нибудь теста – данные события хоть и происходят одно за другим, но незнание ответа на один вопрос никак не зависит от незнания других ответов =) Хотя, закономерности тут, конечно, есть =) Тогда совсем простой пример с неоднократным подбрасыванием монеты – сей увлекательный процесс даже так и называется: повторные НЕзависимые испытания.

Задача 6

Из урны, в которой находится 6 белых и 4 черных шара, извлекаются наудачу один за другим три шара. Найти вероятность того, что:

а) все три шара будут черными;
б) будет не меньше двух шаров черного цвета.

Решение:всего: 6 + 4 = 10 шаров в урне.

Событий в данной задаче будет многовато, и в этой связи целесообразнее использовать смешанный стиль оформления, обозначая прописными латинскими буквами только основные события. Надеюсь, вы уже поняли, по какому принципу подсчитываются условные вероятности.

а) Рассмотрим событие: 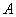– все три шара будут черными.

По теореме умножения вероятностей зависимых событий:

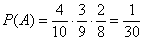
б) Второй пункт интереснее, рассмотрим событие: 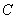– будет не меньше двух шаров черного цвета. Данное событие состоит в 2 несовместных исходах: либо все шары будут чёрными (событие 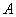) либо 2 шара будут чёрным и 1 белым – обозначим последнее событие буквой .

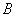Событие 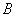включается в себя 3 несовместных исхода:

в 1-м испытании извлечён белый и во 2-м и в 3-м испытаниях – чёрные шары
или
в 1-м испытании извлечён ЧШ и во 2-м – БШ и в 3-м – ЧШ
или
в 1-м испытании извлечён ЧШ и во 2-м – ЧШ и в 3-м – БШ.

По теоремам сложения вероятностей несовместных и умножения вероятностей зависимых событий:
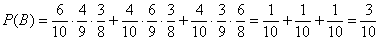– вероятность того, что среди трёх последовательно извлеченных шаров будет 2 чёрных и 1 белый шар.

На всякий случай озвучу примерный ход рассуждений при конструировании, например, произведения :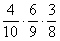
«в 1-м испытании с вероятностью 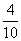извлекается ЧШ, после чего в урне останется 9 шаров, среди которых 6 белых и 3 чёрных. И во 2-м испытании с вероятностью 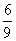извлекается БШ, после чего в урне останется 8 шаров, среди которых 5 белых и 3 чёрных. И, наконец, в 3-м испытании с вероятностью 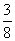будет снова извлечён ЧШ»

По теореме сложения вероятностей несовместных событий:
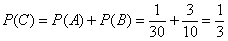– вероятность того, что среди трёх последовательно извлеченных шаров будет не менее двух черных.

Ответ: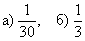

Задача 7

Из 20 экзаменационных билетов 3 содержат простые вопросы. Пять студентов по очереди берут билеты. Найти вероятность того, что хотя бы одному из них достанется билет с простыми вопросами

Решение: рассмотрим события:
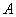– хотя бы одному из пяти студентов достанется билет с простыми вопросами;
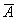– всем пятерым достанутся непростые билеты.
Данные события являются противоположными, поэтому .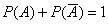
По теореме умножения вероятностей зависимых событий:

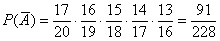
Таким образом: 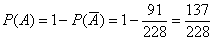– искомая вероятность
Ответ: