I. Общие свойства
13) Область существования функции (множество значений и область определения функции).
14) Непрерывность. Точки разрыва. (Если они имеются).
15) Вертикальные асимптоты
16) Пересечение с осями координат. Интервалы знакопостоянства.
17) Четность. Периодичность.
II. Монотонность. Точки экстремума.
18) Интервалы возрастания и убывания.
19) Точки максимума и минимума.
III. Выпуклость, вогнутость, точки перегиба.
20) Области выпуклости и вогнутости.
21) Точки перегиба. (Если они имеются).
IV. Наклонные асимптоты. Построение графика.
22) Асимптоты. (Если они имеются).
23) Дополнительные точки. (Если надо).
24) Построение графика.
Решение. 1. Общие свойства
1.1. Находим область определения функции: 
функция непрерывна в каждой точке числовой оси и, следовательно, не имеет вертикальных асимптот.
1.2. Находим точки пересечения графика с осями координат:
если 
, то 
;
если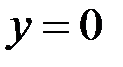 
, то 
или 
.
Таким образом 
– точки пересечения графика с координатными осями.
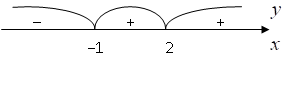
1.3. Находим интервалы знакопостоянства функции.
Функция отрицательна, если 
, при 
функция положительна.
1.4. Проверим, является ли функция четной, нечетной или она является функцией общего вида:
1) 
;
2) Найдем 
. Так как 
функция не является четной. При этом, 
следовательно, свойство нечетности также не выполняется, а значит данная функция общего вида.
1.5. Функция не обладает свойством периодичности.
Исследование функции по первой производной
2.1. Находим первую производную функции:
.
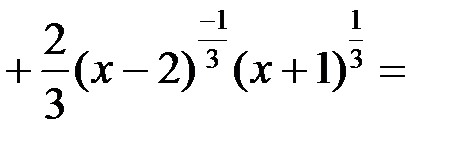
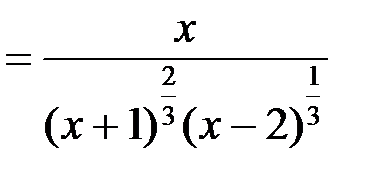2.2. Находим критические точки первого типа, т.е. точки, в которых первая производная равна нулю или не существует: 
– не существует, если 
.
2.3. Находим интервалы возрастания и убывания функции:
Функция возрастает, если 
, при 
функция убывает.
2.4. Находим экстремумы функции:
точка гладкого максимума;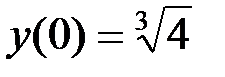 
– максимум функции;
точка пикообразного минимума;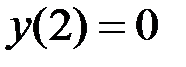 
– минимум функции.
Исследование функции по второй производной
3.1. Находим вторую производную функции (применяя логарифмическое 
дифференцирование)
.
3.2. Находим критические точки для второй производной:
, 
не существует при 
.
3.3. Находим интервалы выпуклости и вогнутости функции:
Функция вогнута, если 
, при 
функция выпукла.
3.4. Находим точки перегиба: 
точка перегиба с вогнутости на выпуклость.
Исследуем функцию на наличие асимптот
4.1. Вертикальных асимптот нет (см. п.1)
4.2. Ищем наклонную асимптоту в виде 
двусторонняя наклонная асимптота.
|
|
|
|
|
|
Задание 4.1. Найти интеграл 
.
Решение. Воспользуемся формулами подведения под знак дифференциала: 
.
Тогда,
.
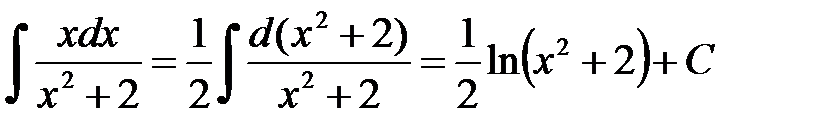Задание 4.2. Найти 
.
Решение.
Используем формулу интегрирования по частям: 
Обозначим 
, тогда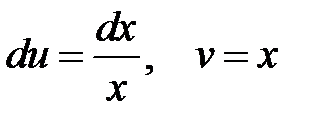 
. Следовательно,
.
Задание 4.3. Вычислить: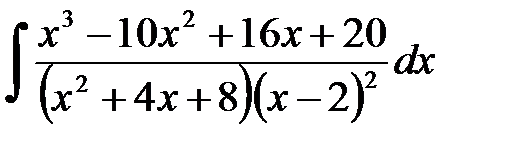 
.
Решение. Дробь 
правильная, так как степень многочлена в числителе строго меньше степени многочлена в знаменателе. Разложим её на сумму простейших дробей: 
.
Найдем неопределенные коэффициенты A, B, C, D. Приведем дроби к общему знаменателю и приравняем числители.
Для нахождения неопределенных коэффициентов используем комбинированный метод, т.е. используем «удобные» значения 
и равенство коэффициентов при одинаковых степенях многочленов.
Из первого равенства: 
. С учетом этого получаем систему трех уравнений с тремя неизвестными:
Используя свойства интегралов, имеем:
Задание 4.4.
а) Найти площадь фигуры, ограниченной линиями
и 
.
Решение. Данная фигура изображена на рисунке. Площадь ее вычислим по формуле 
. Решив систему 
, находим 
, 
, следовательно, 
, 
. На отрезке 
имеем: 
. Значит, в формуле в качестве 
возьмем x, а в качестве 
– 
.
Получим: 
#
б) Найти площадь фигуры, ограниченной линиями , 
, 
, 
Решение. Сделаем чертеж. Данную фигуру можно рассматривать как криволинейную трапецию, ограниченную снизу осью
, слева и справа – прямыми 
и 
, сверху – графиками функций и Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой 
на две части (х =1 – это абсцисса точки пересечения линий и ).
Площадь каждой из этих частей находим по формуле 
:
;
.
Следовательно: 
.
#
в) Найти площадь фигуры, ограниченной линиями 
Решение. Строим фигуру. Видим, что для решения задачи наиболее подходит формула 
.
В нашем случае 
и 
.
При этом 
и 
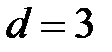, где 
– точка пересечения графиков функций 
и 
.
.
#
г) Найти площадь фигуры ограниченной линиями:
и 
.
Решение: Параметрические уравнения определяют эллипс с полуосями 
. На рисунке представлена фигура, площадь которой надо найти.
Требуется вычислить площадь области, ограниченной эллипсом и прямой 
, находящейся выше этой прямой. Будем искать площадь по формуле: 
, где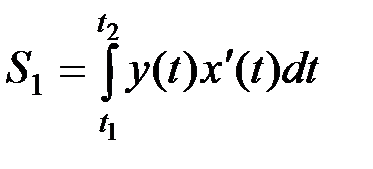 
. Найдём значения параметров 
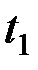и 
, соответствующих точкам пересечения эллипса и прямой. Для этого решим систему уравнений:
Þ 
Параметру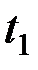 
соответствует значение 
, а параметру 
значение 
. Так как область симметрична относительно оси Оу, то можно найти площадь половины области в пределах от 
до 
, и удвоить это значение. Итак, значению 
соответствует значение параметра 
, тогда 
‒ это площадь прямоугольника, ограниченного осью абсцисс и прямой 
. Стороны прямоугольника 
и 
, а значит его площадь 
.
В итоге получаем: 
#
д) Найти площадь фигуры ограниченной линиями:
Решение. Построим область, ограниченную трёхлепестковой розой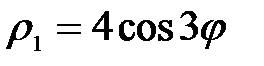 
и окружностью 
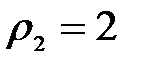радиуса 2, с центром в начале координат.
Найдем точки пересечения данных линий:
С учетом симметрии фигуры можно найти площадь заштрихованной части и умножить на 6.
Воспользуемся формулой 
. В нашем случае: 
Задание 4.5.
а) 
, интеграл сходится.
#
б) 
,
интеграл расходится.