Перевод комплексного числа из одной формы в другую.
Комплексное число можно записать в одной из трех форм:
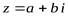– алгебраическая форма;
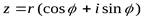– тригонометрическая форма;
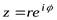– показательная форма.
Для записи комплексного числа в алгебраической форме необходимо знать его действительную часть a и коэффициент при мнимой единице b.
Для тригонометрической и показательной форм – модуль r и аргумент j.
Поэтому для перевода комплексных чисел из одной формы в другую можно предложить следующие алгоритмы.
А) Перевод из алгебраической формы в тригонометрическую и показательную
1. Построить вектор – геометрическое изображение комплексного числа.
2. Отметить на чертеже острый угол a от вектора до ближайшей к нему части оси Ox и угол j – от положительной части оси Ox до вектора.
3. Вычислить модуль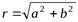 
.
4. Вычислить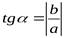 
и определить по его значению острый угол a
5. По найденному значению a и чертежу определить аргумент j
6. Подставить найденные значения модуля и аргумента в запись тригонометрической и показательной форм.
Пример. Записать в тригонометрической и показательной формах комплексное число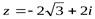 
.
Решение.
На чертеже построен вектор и отмечены углы j и a
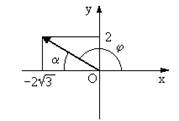Модуль 
.
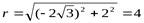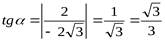, значит a=30°
Из чертежа видно, что j= 180°- a = 150° Поэтому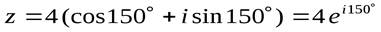 
.
б) Перевод комплексного числа из тригонометрической формы в алгебраическую
1. Вычислить синус и косинус.
2. Раскрыть скобки.
Пример.Записать комплексное число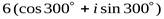 
в алгебраической форме.
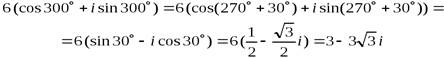Р ешение.
В) Перевод комплексного числа из тригонометрической формы в показательную и наоборот.
В обеих формах комплексное число определяется модулем и аргументом. Поэтому алгоритм перевода состоит из одного действия:
1. Переписать в нужной форме.
Пример.
Записать комплексное число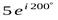 
в тригонометрической форме.
Решение.
Из записи числа видно, что его модуль r = 5 и аргумент j = 200°.
Поэтому тригонометрическая форма числа имеет вид
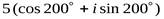
г) Перевод из комплексного числа показательной формы в алгебраическую.
Выше описан перевод комплексного числа из показательной формы в тригонометрическую и из тригонометрической в алгебраическую.
Поэтому алгоритм имеет вид:
1.Выполнить требуемый перевод через тригонометрическую форму.
2. Раскрытие неопределенности. При вычислении некоторых пределов возникает ситуация, которую называют неопределённостью. Например, если f(n) 
и g(n) 
при n 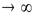, то попытка произвести непосредственное вычисление предела 
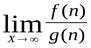приводит к неопределённости 
. Аналогичным образом появляются неопределённости следующих типов: 
; 
; 
; 
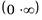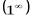и т.п. Для того, чтобы раскрыть неопределенность, требуется применить тот или иной технический приём. В частности, неопределённости 
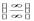обычно исчезает после сокращения дроби на множитель, который определяет наибольшую скорость роста численности или (на выбор) знаменателя. Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть 
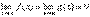или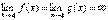 
.Тогда, если существует предел отношения производных этих функций 
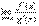, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем 
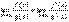.Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Неопределенность типа 
Если при вычислении получается неопределенность типа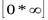 
, то можно использовать правило Лопиталя, преобразовав предварительно выражение следующим образом: 
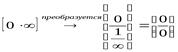или же 
.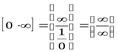