Средняя арифметическая применяется, если известны значения усредняемого признака и количество единиц совокупности с определенным значением признака.
Средняя арифметическая бывает простой и взвешенной.
Простая применяется тогда, когда данные не сгруппированы, а даны в виде перечня.:

Таблица 9
Число дошкольных учреждений и численность детей в них (на конец года)
|


т. е. среднее число дошкольных учреждении в РФ в период с 1999 года по 2004 год составило 41990, средняя численность детей в дошкольных учреждениях РФ – 4290,89 тыс.чел.
Таблица 10
Расходы консолидированного бюджета России на дошкольное образование
| Показатели | ||||
| Численность обучающихся (тыс. чел.) | ||||
| Расходы на одного обучающегося (руб. в год) |
По таблице 10 рассчитаем средние расходы на одного обучающегося за период с 2001 года по 2004 год, для этого используем среднеарифметическую взвешенную:

Рассчитав получим 15384,4 руб. в год на одного обучающегося.
Мода
Мода – наиболее часто встречающаяся в ряду распределения варианта. Она дает представление о центре распределения вариационного ряда.
Для дискретного ряда модой является варианта, обладающая наибольшей частотой.
При исчислении моды для интервального ряда вначале необходимо определить модальный интервал, в пределах которого находится мода, а затем по формуле (формула приведена ниже) определить модальное значение признака.
 , где
, где
 ‑ нижняя граница модального интервала;
‑ нижняя граница модального интервала;
 ‑ величина интервала;
‑ величина интервала;
 ‑ частота модального интервала;
‑ частота модального интервала;
 ‑ частота интервала, предшествующего и следующего за интервалом.
‑ частота интервала, предшествующего и следующего за интервалом.
Медиана
Медиана – это вариант, который приходится на середину вариационного ряда. Медиана делит ряд на две равные части – со значением признака меньше медианы и со значением признака больше медианы. В интервальных рядах она характеризуется тем, что равна накопленной сумме частот, равной или превышающей полусумму всех частот ряда. Значение медианы определяется по формуле:
 , где
, где
x0 – нижняя граница медианного интервала;
h – величина интервала;
Σf – сумма частот или число членов ряда;
Sm-1 – сумма накопленных частот, интервалов, предшествующих медиане;
fm – частота медианного интервала.
Из таблицы 11 получаем:
Мо=2005
Ме=2005
М0 = 2005, т.к. эта варианта имеет наибольшую частоту (38123349,2).
Таблица 11
Расходы на дошкольное образование федерального бюджета России
| Год | Дошкольное образование |
| 462349,8 | |
| 542373,0 | |
| 1139085,2 | |
| 802607,3 | |
| 3812334,2 |
Для расчета медианы найдем полусумму частот, затем определим варианту, в пределах которой лежит данная частота:
6758749,5/ 2 = 3379374,75, тогда Ме = 2005.
2.3.4. Показатели вариациидля дошкольных учреждений
Наряду со средними значениями в статистике применяются показатели вариации, характеризующие отклонение отдельных признаков от общей средней.
К показателям вариации относятся:
1.Размах вариации – наиболее простую меру колеблемости:
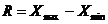
2.среднее линейное отклонение d (средняя арифметическая абсолютных значений отклонений отдельных вариантов от их средней арифметической):
 ;
;
3.Дисперсия (средний квадрат отклонений вариантов от их средней величины):
 ;
;
4.среднее квадратическое отклонение σ(обобщающая характеристика размеров вариации признака в совокупности):
 ;
;
5.коэффициент вариации (выраженное в процентах отношение среднего квадратического отклонения к средней арифметической):
 ;
;
6.коэффициент осцилляции:

Таблица 12
Число дошкольных учреждений в городах и поселках городского типа (на конец года)
 Регион Регион
| Число дошк. учр., 2004 | Расчетные столбцы | |

| 
| ||
| Белгородская область | |||
| Брянская область | |||
| Владимирская область | |||
| Воронежская область | |||
| Ивановская область | |||
| Калужская область | |||
| Костромская область | |||
| Липецкая область | |||
| Московская область | |||
| Орловская область | |||
| Рязанская область | |||
| Смоленская область | |||
| Тамбовская область | |||
| Тверская область | |||
| Тульская область | |||
| Ярославская область | |||

|
Рассчитаем показатели вариации по таблице 12 и получим следующие результаты:
R=1312-132=1180

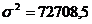

 . Т.к. коэффициент вариации равен 85% следовательно, совокупность неоднородна.
. Т.к. коэффициент вариации равен 85% следовательно, совокупность неоднородна.

Выборочное наблюдение
Статистика имеет дело с массовыми совокупностями, поэтому статистические исследования очень трудоемки. Следовательно, целесообразна замена сплошного наблюдения выборочным.
Выборочное наблюдение – это такое несплошное наблюдение единиц изучаемой совокупности отобранных случайным образом.
Целью выборочного наблюдения является получение обобщающих показателей генеральной совокупности на основе выборочных характеристик (средних и относительных).
При выборочном наблюдении надо учитывать, на сколько обобщающая характеристика генеральной совокупности отличается от соответствующей характеристики выборки, то есть ошибку выборочного наблюдения
Для проведения расчетов необходимо оговорить определенные условия проведения исследования:
1. Коэффициент доверия (t)
2. Средняя ошибка репрезентативности ( )
)
3. Среднее квадратическое отклонение (σ) и т.д.
Пример: В городе проживает 1500 матерей одиночек с одним ребенком в возрасте от 1 года до 6 лет. Планируется провести безповторную случайную выборку для выявления числа детей посещающих детский сад, при средне квадратическом отклонении равном 25 человек.
Необходимо определить объем выборки при котором предельная ошибка не будет превышать 5 человек с вероятностью: 1) 0,683; 2) 0,954; 3) 0,997.
Решение.
Предельная ошибка выборки при бесповторном отборе рассчитывается по следующей формуле: 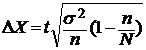
Выразим отсюда выборочную совокупность: 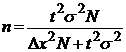
a) Ф(t)=0,683 t=1 
b) Ф(t)=0,954 t=2 
c) Ф(t)=0,997 t=3 
Полученные результаты показывают, что чем более достоверными должны быть результаты выборочного наблюдения, тем больше должен быть размер выборки.