Ряд динамики – последовательность одноименных показателей, расположенных в хронологическом порядке и характеризующих развитие изучаемого явления. Уровни ряда могут задаваться абсолютными, относительными и средними величинами.
Аналитические показатели характеризуют изменение уровней ряда в отчетном периоде по сравнению с предыдущим. В случае, когда сравнение проводится с периодом времени, начальным в ряду динамики, получают базисные показатели (с постоянной базой сравнения). Если же сравнение производится с периодом времени, непосредственно предшествующим отчетному, то говорят о цепных показателях (с переменной базой сравнения).
Абсолютный прирост характеризует темпы увеличения или уменьшения исследуемого явления за определённый промежуток времени.
а) цепной б) базисный
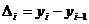

Темп роста – отношение данного уровня явления к предыдущему (цепной темп роста) или начальному (базисный темп роста) выраженное в процентах.
а) цепной б) базисный


Темп прироста – отношение абсолютного прироста к предыдущему или начальному уровню, выраженному в процентах. Темп прироста можно рассчитать по данным о темпе роста, для этого от темпа роста необходимо отнять 100 или от коэффициента роста 1.
а) цепной б) базисный


Абсолютное значение одного процента прироста – отношение абсолютного прироста к темпу прироста.
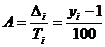
Рассчитаем основные показатели рядов динамики на основании данных, приведенных в таблице 13.
Таблица 13
Обеспеченность местами детей, находящихся в дошкольных учреждениях (на 100 мест приходится детей) в РФ

| ||||||
| Число детей на 100 мест |
Таблица 14
Динамика обеспеченности местами детей, находящихся в дошкольных учреждениях (на 100 мест приходится детей)
| годы | численность детей, приходящихся на 100 мест в дошкольных учреждениях | Абсолютный прирост | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста | ||||
| цепной | базисный | цепной | базисный | цепной | базисный | ||||
| - | - | - | - | - | - | - | |||
| 103,8 | 103,8 | 3,8 | 3,8 | 0,789 | |||||
| 101,2 | 105,1 | 1,2 | 5,1 | 0,83 | |||||
| 103,6 | 108,9 | 3,6 | 8,9 | 0,83 | |||||
| 102,3 | 111,4 | 2,3 | 11,4 | 0,87 | |||||
| 104,5 | 116,5 | 4,5 | 16,5 | 0,89 |
Судя по полученным данным, число детей приходящихся на 100 мест в детском саду с каждым годом неуклонно растет. Так с 1999 года прирост составил 16,5%. Исходя из данных, рассчитанных в таблице 14, можно сделать вывод, что рост не прекратится, а только ускорится, и в скором времени мест в ДОУ будет не хватать.
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. С этой целью ряды динамики подвергаются обработки одним из следующих методов:
1. Приведение рядов к одному основанию.
2. Разбивка ряда на короткие периоды.
3. Сглаживание способом скользящих (подвижных) средних.
4. Метод аналитического выравнивания.
1.Приведение ряда к одному основанию. Суть этого метода в том, что показатели каждого ряда выражаются в % к первому или любому другому члену ряда.
Из таблицы 15 видно, что численность детей приходящихся на 100 мест в ДОУ с каждым годом растет, причем как в городах, так и в сельской местности.
Таблица 15
Обеспеченность местами детей, находящихся в дошкольных учреждениях
(на 100 мест приходится детей)
| всего | город | село | В % к 1999 году | |||
| всего | город | село | ||||
| 103,8 | 103,5 | 103,3 | ||||
| 105,1 | 105,9 | 108,3 | ||||
| 108,9 | 108,2 | 111,7 | ||||
| 111,4 | 111,8 | |||||
| 116,5 | 116,5 |
2. Разбивка ряда на короткие периоды. Для выявления тенденций длинных колеблющихся рядов их разбивают на более короткие периоды, а затем определяют уровень по каждому периоду.
3. Сглаживание способом скользящих (подвижных) средних применяют с целью сглаживания колеблемостим, вызванной действием случайных величин.
Таблица 16
Обеспеченность местами детей, находящихся в дошкольных учреждениях
(на 100 мест приходится детей)
| год | число детей, приходящихся на 100 мест в дошкольных учреждениях | Подвижные средние | |
| за два года | за три года | ||
| 80,5 | 81,3 | ||
| 82,5 | 83,7 | ||
| 84,5 | 85,7 | ||
| 88,7 | |||
Иллюстрация действия данного метода представлена на рисунке 3. На графике заметно постепенное сглаживание линий.

Рис. 3. Метод скользящих средних.
4. Метод аналитического выравнивания. Суть этого метода заключается в нахождении такого уровня плавного движения ряда, который, приближаясь к первоначальному (эмпирическому ряду), будет наиболее полно характеризовать основную тенденцию динамики. Для этого уровни ряд уусловно рассматриваются как функция времени t, а фактические уровни ряда заменяются такими теоретическими, которые наименее отклоняются от эмпирических. Выравнивание происходит по методу наименьших квадратов.
В зависимости от года t число детей приходящихся на 100 мест в ДОУ изменяется по закону:
Yтеор. = a0+a1t, где a0, a1 – параметры уравнения регрессии.
Найдем параметры уравнения регрессии, решив систему уравнений, составленную по методу наименьших квадратов:

Промежуточные значения расчетов приведены в таблице 17.
Таблица 17
| год | № | число детей приходящихся на 100мест в ДОУ | t2 | t*y | Yтеор |
| 78,857 | |||||
| 82,314 | |||||
| 83,771 | |||||
| 86,228 | |||||
| 88,685 | |||||
| 91,142 | |||||
| Итог | 510,997 |
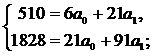

Значит Yтеор.=76,4 + 2,457t
Полученные данные изображены на рисунке 4.
Линия Yтеор., сглаживая колебания конкретных значений уровня, четко отображает неуклонный рост числа детей приходящихся на 100 мест в ДОУ.

Рис. 4.Фактическое и расчетное число детей приходящихся на 100мест в ДОУ
Корреляционный анализ
Корреляция - это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
Основными задачами корреляционного анализа является определение формы и количественной характеристики связи, количественное определение тесноты связи между двумя признаками.
Если связь линейная, то теснота связи оценивается линейным коэффициентом корреляции:
 ,
,
Исследование взаимосвязи числа родившихся и численности детей в ДОУ проведем на основе данных приведенных в таблице 18.
Таблица 18
Число родившихся и численность детей в ДОУ
| № | Год | родившихся, тыс чел. (X) | Числ-ть детей в ДОУ, тыс. чел., (Y) |
| 1311,6 | 4246,3 | ||
| 1397,0 | 4267,3 | ||
| 1477,3 | 4321,27 | ||
| 1502,5 | 4422,57 | ||
| ИТОГ | 5688,4 | 25745,34 |
Предположим, что форма взаимосвязи этих показателей является линейной, т.е. ее можно представить в виде: у=а0+а1х, где х – число родившихся, у – число детей в ДОУ.
Определим параметры уравнения регрессии, для этого используем метод наименьших квадратов.

Расчеты приведены в таблице 19.
Таблица 19
| Год | x | y | 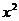
| xy 
| Y |
| 1311,6 | 4246,3 | 1720294,56 | 5569447,08 | 4315,3556 | |
| 1397,0 | 4267,3 | 5961418,1 | 4314,587 | ||
| 1477,3 | 4321,27 | 2182415,29 | 6383812,171 | 4313,8643 | |
| 1502,5 | 4422,57 | 225706,25 | 6644911,425 | 4313,6375 | |
| ИТОГ | 5688,4 | 17257,44 | 6080025,10 | 24559588,78 | 17257,4444 |


Итак, уравнение регрессии имеет вид:


Рис.5. График регрессии
Определим тесноту связи между числом родившихся и численностью детей в ДОУ, для этого вычислим линейный коэффициент корреляции  . Расчеты представлены в таблице 20.
. Расчеты представлены в таблице 20.
Таблица 20
| № | X | Y | 
| 
| 
| 
| 
|
| 1311,6 | 4246,3 | -110,5 | -68,06 | 7520,63 | 12210,25 | 4632,1636 | |
| 1397,0 | 4267,3 | -25,1 | -47,06 | 1181,206 | 630,01 | 2214,6436 | |
| 1477,3 | 4321,27 | 55,2 | 6,91 | 381,432 | 3047,04 | 47,7481 | |
| 1502,5 | 4422,57 | 80,4 | 108,21 | 8700,084 | 6464,16 | 11709,4041 | |

| 5688,4 | 17257,44 | 17783,35 | 22351,46 | 18603,9594 |

Полученное значение линейного коэффициента корреляции говорит о наличии высокой прямой связи между изучаемыми явлениями, т.е. при увеличении числа родившихся увеличивается и численность детей в ДОУ и, наоборот, с уменьшением числа родившихся уменьшается и численность детей в ДОУ.