Вычислим абсолютное ускорение точки  . Для этого возьмем полную производную по времени от абсолютной скорости (5.7):
. Для этого возьмем полную производную по времени от абсолютной скорости (5.7):
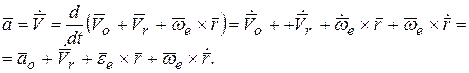 (5.9)
(5.9)
Здесь  – ускорение полюса
– ускорение полюса 
 подвижной системы координат,
подвижной системы координат, 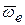 – вектор угловой переносной скорости,
– вектор угловой переносной скорости,  вектор углового переносного ускорения.
вектор углового переносного ускорения.
Вычислим полные производные по времени от векторов 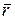 и
и  (используя полученные ранее выражения (5.4, а) и (5.5)):
(используя полученные ранее выражения (5.4, а) и (5.5)):
 ;
;
 (5.10)
(5.10)
Подставляя (5.10) в (5.9), получим
 . (5.11)
. (5.11)
В формуле (5.11) подчеркнутые слагаемые характеризуют движение подвижной системы координат, т.е. составляют переносное ускорение
 , (5.12)
, (5.12)
здесь, согласно формулам Эйлера,
 ,
,  .
. 
Напомним, что переносное ускорение точки – это ускорение точки жестко скрепленной с подвижной системой координат и не имеющей в рассматриваемый момент времени относительного движения.
Второе слагаемое в (5.11) –  , соответствует ускорению относительного движения.
, соответствует ускорению относительного движения.
Оставшиеся не подчеркнутые слагаемые в (5.11) определяют ускорение, которое принято называть ускорением Кориолиса, обозначим это ускорение  , Тогда
, Тогда
 . (5.13)
. (5.13)
Учитывая все замечания, выражение (5.11) перепишется
 . (5.14)
. (5.14)
Полученное выражение определяет теорему Кориолиса: абсолютное ускорение точки является векторной суммой трех ускорений: относительного, переносного и ускорения Кориолиса.
Примечание
Для выяснения физической сущности ускорения Кориолиса рассмотрим движение в плоскости вращения. Нас будет интересовать движение точки с постоянной относительной скоростью  вдоль радиуса стержня (рис. 5.4).
вдоль радиуса стержня (рис. 5.4).
 Рис. 5.4
Рис. 5.4
|
На рисунке указаны положения точки  и
и 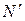 в два момента времени, разделенных промежутком Dt, в течении которого радиус повернется на угол Da=wt. Относительная скорость
в два момента времени, разделенных промежутком Dt, в течении которого радиус повернется на угол Da=wt. Относительная скорость  – скорость вдоль радиуса изменяется за это время только по направлению, а переносная скорость
– скорость вдоль радиуса изменяется за это время только по направлению, а переносная скорость  , перпендикулярная радиусу, изменяется как по направлению, так и по модулю
, перпендикулярная радиусу, изменяется как по направлению, так и по модулю 
 ,
,  для положения точек
для положения точек  и
и 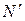 соответственно.
соответственно.
Модуль полного изменения абсолютной скорости, перпендикулярной радиусу (направлению 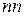 ), равен
), равен

где учтено, что для 


 ,
,  .
.
Изменение скорости характеризуется ускорением, следовательно, ускорение Кориолиса согласно определению ускорения, по модулю равно:

Получили, что изменение модуля абсолютной скорости характеризуется ускорением

Ускорение Кориолиса обусловлено различным значением переносной скорости в разных точках подвижной системы координат. Иначе говоря, ускорение Кориолиса является результатом взаимного влияния двух движений – переносного и относительного.
§ 5.4. Способы вычисления  ,
,  и
и  ускорений
ускорений
Относительное ускорение  . Движение подвижных осей во внимание не принимается, наблюдатель находится внутри подвижной системы координат
. Движение подвижных осей во внимание не принимается, наблюдатель находится внутри подвижной системы координат  .
.
Вычисление  зависит от способа задания относительного движения ():
зависит от способа задания относительного движения ():
– координатный способ задания относительного движения точки М
 .
.
– естественный способ задания относительного движения. Приводим оси естественного трехгранника 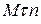 к движущейся точки
к движущейся точки  , тогда
, тогда
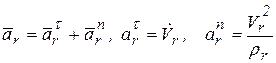 ,
,
здесь  – радиус кривизны относительной траектории в точке М.
– радиус кривизны относительной траектории в точке М.
Вектор относительного ускорения расположен в соприкасающейся плоскости относительного движения.
Переносное ускорение  . Точка жесткосвязана с телом (
. Точка жесткосвязана с телом ( ) и движется вместе с ним относительно неподвижной системы координат
) и движется вместе с ним относительно неподвижной системы координат 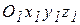 . Наблюдатель находится внутри неподвижной системы координат.
. Наблюдатель находится внутри неподвижной системы координат.
1. Подвижная система координат движется поступательно – 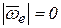 ,
,  , тогда переносное ускорение точки М, согласно (5.12)
, тогда переносное ускорение точки М, согласно (5.12)

Переносное ускорение совпадает с ускорением подвижной системы координат.
2. Подвижная система координат вращается относительно неподвижной оси  с угловой скоростью
с угловой скоростью  и угловым ускорением
и угловым ускорением  . В этом случае
. В этом случае  =0, тогда из (5.12), переносное ускорение точки М, согласно (5.12)
=0, тогда из (5.12), переносное ускорение точки М, согласно (5.12)
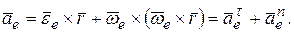
Если точка в переносном движении движется по окружности радиуса  , то
, то
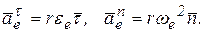
Векторы ускорений  расположены в соприкасающейся плоскости переносного движения, т.е. в плоскости, перпендикулярной оси вращения.
расположены в соприкасающейся плоскости переносного движения, т.е. в плоскости, перпендикулярной оси вращения.
Ускорения Кориолиса 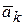 . Ускорение Кориолиса вычисляется по формуле:
. Ускорение Кориолиса вычисляется по формуле:  , здесь
, здесь  . Модуль ускорения Кориолиса равен
. Модуль ускорения Кориолиса равен

 здесь угол
здесь угол  , угол между вектором относительной скорости
, угол между вектором относительной скорости 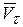 и вектором угловой скорости переносного вращения
и вектором угловой скорости переносного вращения  .
.
Для вычисления направления  , удобно пользоваться правилом Жуковского. Пусть имеем точку М, движущуюся с относительной скоростью
, удобно пользоваться правилом Жуковского. Пусть имеем точку М, движущуюся с относительной скоростью 
(рис. 5.5). Построим плоскость (П), перпендикулярную вектору угловой скорости переносного вращения  . Спроецируем
. Спроецируем 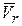 на плоскость (П). Проекцию обозначим
на плоскость (П). Проекцию обозначим  . Она является скаляром и равна
. Она является скаляром и равна
 ,
,
тогда
 . (5.12)
. (5.12)
Правило Жуковского: ч тобы получить направление ускорения Кориолиса  , следует проекцию вектора относительной скорости , следует проекцию вектора относительной скорости  повернуть на 90° вокруг оси, параллельной оси переносного вращения повернуть на 90° вокруг оси, параллельной оси переносного вращения  , в направлении этого вращения. , в направлении этого вращения.
|
Рассмотрим случаи обращения в нуль ускорения Кориолиса.
Ускорение Кориолиса равно нулю, если:
1.  – переносное движение является поступательным;
– переносное движение является поступательным;
2.  – в те моменты времени, в которые происходит изменение направления относительного движения;
– в те моменты времени, в которые происходит изменение направления относительного движения;
3.  – когда
– когда  ║
║  .
.
Примеры решения задач
Пример 5.2. В примере 5.1. вычислить абсолютное ускорение.
Решение. Рассмотрим стержень, который вращается в плоскости  вокруг неподвижного центра
вокруг неподвижного центра  с угловой скоростью
с угловой скоростью  . Точка М скользит вдоль стержня со скоростью
. Точка М скользит вдоль стержня со скоростью 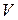 , рис. 5.6.
, рис. 5.6.
Рис. 5.6 
| Абсолютное ускорение точки является векторной суммой трех ускорений: относительного, переносного и ускорения Кориолиса.
 .
Здесь: .
Здесь:
|
– вектор относительного ускорения  , т.к.
, т.к.  ;
;
– вектор переносного ускорения
 ,
,
где  ,
,  .
.
Вектор  направлен пооси
направлен пооси  ;
;
– ускорение Кориолиса 
Определим направление вектора 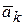 , используя правило Жуковского. Угол между вектором относительной скорости
, используя правило Жуковского. Угол между вектором относительной скорости 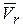 и
и  равен
равен  (вектор
(вектор  ), тогда вектор
), тогда вектор 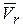 разворачиваем на
разворачиваем на  по направлению дуговой
по направлению дуговой
стрелки  (рис. 5.6).
(рис. 5.6).
Вычислим абсолютное ускорение точки  :
:
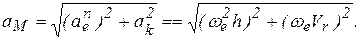
Угол между  и осью
и осью  равен.
равен.
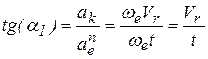 ,
,  .
.
Пусть  ,
,  ,
,  ,
,
тогда  ,
, 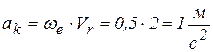 ,
,

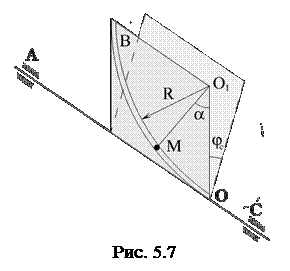
 .
.
Пример 5.3. Пластина В вращается вокруг неподвижной оси  , согласно уравнению
, согласно уравнению  (рис. 5.7).
(рис. 5.7).
На пластине по желобу движется точка, согласно уравнению
 .
.
Вычислить абсолютную скорость и абсолютное ускорение точки М в момент времени t = 1с, если радиус желоба  .
.
Решение. Будем считать, что в момент времени t = 1с угол поворота  имеет такое значение, при котором тело В располагается в плоскости
имеет такое значение, при котором тело В располагается в плоскости  , рис. 5.8.
, рис. 5.8.
 Точка М совершает сложное движение, состоящее из относительного (движение точки по желобу) и переносного (вращение точки вместе с пластиной вокруг оси АС) движений.
Точка М совершает сложное движение, состоящее из относительного (движение точки по желобу) и переносного (вращение точки вместе с пластиной вокруг оси АС) движений.
Вычислим абсолютную скорость точки  :
:
 .
.
 Относительная скорость
Относительная скорость  . Найдем положение точки М на пластине В через 1с. Для этого вычислим значение дуговой координаты
. Найдем положение точки М на пластине В через 1с. Для этого вычислим значение дуговой координаты 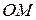 при
при  :
:


Если обозначить угол между радиусами 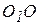 и
и  , через a тогда
, через a тогда
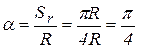 .
.
Относительное движение точки задано естественным способом. Приведем оси  к точке М на траектории. Относительная скорость
к точке М на траектории. Относительная скорость 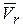 точки М при
точки М при 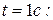

Вектор относительной скорости  лежит в соприкасающейся плоскости
лежит в соприкасающейся плоскости
относительного движения – плоскость  и направлена по касательной к траектории относительного движения – по оси
и направлена по касательной к траектории относительного движения – по оси  (рис. 5.9, а).
(рис. 5.9, а).
Переносная скорость  . В переносном движении точка движется в соприкасающейся плоскости переносного движения – плоскости
. В переносном движении точка движется в соприкасающейся плоскости переносного движения – плоскости 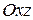 по окружности радиусом
по окружности радиусом  (рис. 5.9, б).
(рис. 5.9, б).

Рис.5.9
Задано уравнение вращения пластины В –  , тогда
, тогда
 .
.
Переносное движение ускоренное, т.к.  > 0,
> 0,  > 0, дуговые стрелки
> 0, дуговые стрелки  и
и 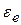 направлены в одну сторону (рис. 5.9, б). Приведем оси
направлены в одну сторону (рис. 5.9, б). Приведем оси  к точке М в плоскости
к точке М в плоскости  .
.
Вычислим радиус кривизны траектории при переносном движении точки М в момент времени 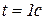 (
( ):
):
 = R -
= R -  = R(1 - cosa) = 30(1 – cos(
= R(1 - cosa) = 30(1 – cos( )) = 30(1 – 0,707) = 8,79 см.
)) = 30(1 – 0,707) = 8,79 см.
Переносная скорость Vе
 .
.
Вектор переносной скорости  направлен по касательной к траектории в точке М – ось
направлен по касательной к траектории в точке М – ось  (рис. 5.9, б). Направление оси
(рис. 5.9, б). Направление оси  согласуется с направлением дуговой стрелки
согласуется с направлением дуговой стрелки  .
.
Так как в данном случае векторы  взаимно перпендикулярны, (вектор скорости
взаимно перпендикулярны, (вектор скорости  расположен в плоскости
расположен в плоскости 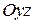 , вектор скорости
, вектор скорости  направлен по оси
направлен по оси  , т.е.
, т.е.  ), то модуль абсолютной скорости точки М
), то модуль абсолютной скорости точки М
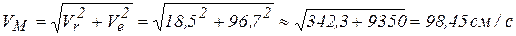 .
.
Вычислим абсолютное ускорение точки М. Абсолютное ускорение точки равно геометрической сумме относительного, переносного и Кориолисово ускорений
 .
.
Относительное ускорение  . Относительное движение точки задано естественным способом – точка
. Относительное движение точки задано естественным способом – точка  движется по окружности радиусом
движется по окружности радиусом  в соприкасающейся плоскости относительного движения
в соприкасающейся плоскости относительного движения  . Приведем к точке
. Приведем к точке  оси естественного трехгранника
оси естественного трехгранника  (рис. 5.10, а). Ось
(рис. 5.10, а). Ось  совпадает с направлением
совпадает с направлением  , ось
, ось  перпендикулярна оси
перпендикулярна оси  и направлена вовнутрь вогнутости траектории по радиусу
и направлена вовнутрь вогнутости траектории по радиусу  .
.

Рис. 5.10
Относительное ускорение  равно
равно
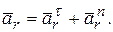
Здесь, при t = 1 с:

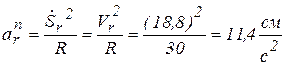 .
.
Точка  движется с замедлением, поскольку векторы
движется с замедлением, поскольку векторы 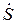 >0,
>0,  <0, вектор
<0, вектор  и вектор
и вектор  имеют разное направление по оси
имеют разное направление по оси  . Вектор
. Вектор  и вектор
и вектор  направлены по осям
направлены по осям  и
и  соответственно и лежат в плоскости
соответственно и лежат в плоскости 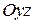 .
.
Переносное ускорение  . Движение точки в ее переносном движении – криволинейное. Точка движется по окружности радиусом
. Движение точки в ее переносном движении – криволинейное. Точка движется по окружности радиусом  в соприкасающейся плоскости переносного движения
в соприкасающейся плоскости переносного движения 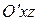 . Приведем к точке
. Приведем к точке  оси естественного трехгранника
оси естественного трехгранника  (рис 5.8, б). Ось
(рис 5.8, б). Ось  совпадает с направлением
совпадает с направлением  , ось
, ось  перпендикулярно оси
перпендикулярно оси  и направлена вовнутрь вогнутости, т.е. по радиусу МК.
и направлена вовнутрь вогнутости, т.е. по радиусу МК.
Переносное ускорение, рис. 5.10, б:
 .
.
Здесь, при t = 1 с:
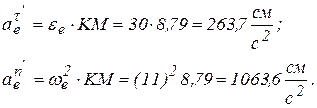
Вектор  и вектор
и вектор 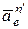 направлены по осям
направлены по осям  и
и  соответственно.
соответственно.
Ускорение Кориолиса  . Вектор ускорения Кориолиса
. Вектор ускорения Кориолиса
 ,
,
его модуль
 .
.
Вектор  направлен по оси вращения АС. Угол
направлен по оси вращения АС. Угол  , угол между векторами
, угол между векторами  и
и  равен
равен  (рис. 5.11, а).
(рис. 5.11, а).
Итак,


Рис. 5.11
Направление вектора  по правилу Журавского: поворачиваем
по правилу Журавского: поворачиваем  на 90° по направлению дуговой стрелке
на 90° по направлению дуговой стрелке 
 вектор
вектор  направлен параллельно оси
направлен параллельно оси  (рис. 5.11, б).
(рис. 5.11, б).
Для вычисления модуля абсолютного ускорения используем способ проекций. Спроецируем все составляющие абсолютного ускорения на оси  . Имеем (рис. 5.10 и рис. 5.11, б):
. Имеем (рис. 5.10 и рис. 5.11, б):



Модуль абсолютного ускорения (рис. 5.12):

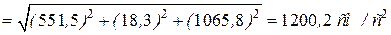
Рис. 5.12 
| Направление вектора  определим геометрически. Совместим с точкой определим геометрически. Совместим с точкой  декартову систему координат декартову систему координат  (рис.5.12). Отложим проекции (рис.5.12). Отложим проекции  абсолютного ускорения на оси координат абсолютного ускорения на оси координат  , построим вектор , построим вектор  . .
|
Пример 5.4. Шар радиусом R=1м вращается вокруг вертикальной оси  по заданному уравнению
по заданному уравнению 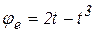 (рад). По меридиану шара движется точка М по заданному уравнению
(рад). По меридиану шара движется точка М по заданному уравнению  (м), рис. 5.13. Дуга
(м), рис. 5.13. Дуга  отсчитывается от точки МО меридиана. Вычислить абсолютную скорость и абсолютное ускорение точки М в момент времени t=1 с.
отсчитывается от точки МО меридиана. Вычислить абсолютную скорость и абсолютное ускорение точки М в момент времени t=1 с.
Решение. За переносное движение точки  примем ее вращение вместе с шаром вокруг оси
примем ее вращение вместе с шаром вокруг оси  (рис. 5.13).
(рис. 5.13).
 Рис. 5.13
Рис. 5.13
| Тогда относительным движением точки будет движение точки по меридиану шара.
Определим положение точки М на меридиане в момент времени t=1с. Имеем:
 .
Так как R=1 м, то положение точки определяется углом широты: .
Так как R=1 м, то положение точки определяется углом широты:

|
Совместим декартову систему координат  с положением точки М при
с положением точки М при  , так, чтобы было М
, так, чтобы было М  , ось Мх проходила через точку С
, ось Мх проходила через точку С
(рис. 5.13). В переносном движении точка движется в соприкасающейся плоскости  . В относительном движении точка движется в соприкасающейся плоскости относительного движения
. В относительном движении точка движется в соприкасающейся плоскости относительного движения  .
.
Вычислим угловую скорость и угловое ускорения переносного движения:
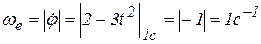 ;
;
 .
.
Знак (–) при  показывает, что вращение шара происходит по часовой стрелке. Одинаковые знаки при
показывает, что вращение шара происходит по часовой стрелке. Одинаковые знаки при 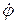 и
и  , показывают, что вращение шара в рассматриваемый момент времени является ускоренным.
, показывают, что вращение шара в рассматриваемый момент времени является ускоренным.
Вычислим модуль скорости переносного движения (при t=1с) – 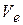 . Жестко скрепляем точку
. Жестко скрепляем точку 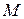 с шаром, точка будет двигаться по окружности радиусом
с шаром, точка будет двигаться по окружности радиусом  в плоскости
в плоскости  (рис. 5.14, а). Тогда
(рис. 5.14, а). Тогда


|
Рис. 5.14
Приведем оси естественного трехгранника  к точке
к точке 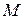 в плоскости
в плоскости  . Вектор скорости переносного движения
. Вектор скорости переносного движения  будет направлен по касательной
будет направлен по касательной  . Оси
. Оси  и
и  определяют соприкасающуюся плоскость переносного движения и совпадают с осями
определяют соприкасающуюся плоскость переносного движения и совпадают с осями  и
и 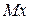 соответственно.
соответственно.
В относительном движении точка движется в соприкасающейся плоскости  относительного движения (рис. 5.14, б). Приведем оси естественного трехгранника
относительного движения (рис. 5.14, б). Приведем оси естественного трехгранника  в плоскости
в плоскости  . Скорость относительного движения точки – это скорость точки М при ее движении вдоль меридиана. Вычислим:
. Скорость относительного движения точки – это скорость точки М при ее движении вдоль меридиана. Вычислим:

 Знак (+) при
Знак (+) при  указывает, что вектор
указывает, что вектор 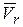 направлен в сторону возрастания дуговой координаты
направлен в сторону возрастания дуговой координаты 
(рис. 5.14, б).
Вычислим абсолютную скорость точки
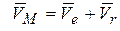 .
.
Модуль абсолютной скорости
 .
.
Направление  вычислим
вычислим
Рис. 5.15 геометрически, рис. 5.15.
Вычислим абсолютное ускорение точки 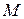
 . (а)
. (а)
Точка М вращается вместе с шаром вокруг неподвижной оси  в плоскости
в плоскости  . Вычислим переносное ускорение
. Вычислим переносное ускорение

Модуль нормального ускорения
 .
.
Ускорение 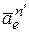 направлено по оси
направлено по оси  (рис. 5.16, а).
(рис. 5.16, а).
Модуль касательной составляющей ускорения
 .
.
 Рис. 5.16
Рис. 5.16
|
Ускорение  направлено по оси
направлено по оси  исовпадает с направлением вектора переносной скорости
исовпадает с направлением вектора переносной скорости  (рис. 5.16, а).
(рис. 5.16, а).
Вектор относительного ускорения расположен в плоскости  (рис.5.16, б).
(рис.5.16, б).
 .
.
Модуль нормальной составляющей относительного ускорения

Ускорение  направлено по оси
направлено по оси  , т.е. к центру шара О (рис. 5.16, б).
, т.е. к центру шара О (рис. 5.16, б).
Модуль касательной составляющей относительного ускорения
 .
.
Вектор ускорения  направлен по оси
направлен по оси  . Так как
. Так как  >0, то вектор
>0, то вектор  направлен в сторону возрастающих значений
направлен в сторону возрастающих значений  S (рис. 5.16, б).
S (рис. 5.16, б).
Вычислим ускорение Кориолиса 
 ,
,
Направление вектора  определим по правилу Жуковского (рис. 5.16, в). Вектор угловой скорости
определим по правилу Жуковского (рис. 5.16, в). Вектор угловой скорости  направлен против оси вращения
направлен против оси вращения 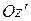 (
( <0). Спроецируем на соприкасающуюся плоскость переносного движения
<0). Спроецируем на соприкасающуюся плоскость переносного движения  вектор
вектор 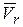 и повернем полученную проекцию
и повернем полученную проекцию  вокруг оси Мz в плоскости
вокруг оси Мz в плоскости  на
на  в сторону дуговой стрелки
в сторону дуговой стрелки 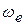 (рис. 5.13, в). Ускорение Кориолиса
(рис. 5.13, в). Ускорение Кориолиса  направлено по оси Му и совпадает с направлением ускорения
направлено по оси Му и совпадает с направлением ускорения  .
.
Для вычисления модуля абсолютного ускорения  используем способ проекций. Спроецируем все составляющие абсолютного ускорения на оси
используем способ проекций. Спроецируем все составляющие абсолютного ускорения на оси  .
.
Имеем (рис. 5.16, а, б, в):
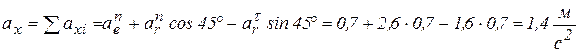 ;
;  ;
;
 .
.
Модуль абсолютного ускорения
 .
.
Направление вектора  вычислим по направляющим косинусам.
вычислим по направляющим косинусам.
 ,
,  ;
;
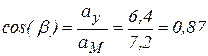 ,
, 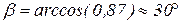 ;
;
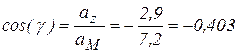 ,
,  .
.
Ответ.  ;
;  .
.