ИССЛЕДОВАНИЕ ИСХОДНОЙ СИСТЕМЫ

Анализ исходной САУ сводится к определению её точности, запаса устойчивости и быстродействия. Для решения этих задач необходимо в первую очередь получить ПФ разомкнутой системы W (s), которая равна произведению ПФ всех звеньев замкнутого контура регулирования. В частности, для структуры, приведенной на рис. 4.1, имеем:

или

,

где K = K_С K_В K_У K_Э K_Г K_Д K_P =1.584 – коэффициент передачи разомкнутой системы.

Передаточной функции разомкнутой системы соответствует tf-модель, получаемая перемножением tf-моделей передаточных функций всех звеньев замкнутого контура САУ. В рассматриваемом случае получим:

>> W=Wd*We*Wg*Wr*Wc*Wv*Wy

Transfer function:

1.584

----------------------------------------------------------------------------------------

2.88e-005 s^6 + 0.00529 s^5 + 0.08456 s^4 + 0.5012 s^3 + 1.206 s^2 + s

Оценка точности исходной системы

Точность работы следящей системы необходимо оценивать ошибкой обработки входного воздействия 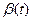, представленного в задании на проектирование максимальной скоростью и максимальным ускорением ε_м. По этим двум параметрам можно сформировать гармоническое входное воздействие

,

где – амплитудное значение ;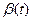

– частота гармонического воздействия.

Пусть Ω _м =17 град/с = 0.2967 рад/с, ε_м =15 град/с² = 0.2618 рад/с². Введем эти параметры в среду MatLab:

>> qm=0.2967 % ввод максимальной скорости

qm =

0.2967

>> еm=0.2618 % ввод максимального ускорения

еm =

0.2618

Определим амплитудное значение и частоту эквивалентного гармонического воздействия :

>> Bm=(qm^2)/еm

Bm =

0.3363

>> wk=еm/qm

wk =

0.8824

Ошибка слежения определяется уравнением

,

где – передаточная функция для ошибки по входному воздействию :

,

где W(s) – ПФ разомкнутой системы.

Для определения целесообразно воспользоваться функцией feedback (W ₁, W ₀), применяемой для вычисления ПФ встречно-параллельного соединения двух звеньев, где W ₁ – охватываемая модель, W ₀ – модель отрицательной обратной связи. В рассматриваемом примере tf-модель ПФ для ошибки получается следующим образом. Полагая W ₁=1, а W ₀= W (s), получим:

>> Fe=feedback(1,W)

Transfer function:

2.88e-005 s^6 + 0.00529 s^5 + 0.08456 s^4 + 0.5012 s^3 + 1.206 s^2 + s

--------------------------------------------------------------------------------------------------

2.88e-005 s^6 + 0.00529 s^5 + 0.08456 s^4 + 0.5012 s^3 + 1.206 s^2 + s + 1.584

Учитывая, что при гармоническом входном воздействии 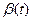рассогласование также изменяется гармонически, можно воспользоваться частотным методом оценки точности. Для определения значения частотной передаточной функции при , удобнее всего воспользоваться функцией freqresp (Fe,wk).

Для рассматриваемого примера получим следующее максимальное значение ошибки :

>> Em=freqresp(Fe,wk)*Bm

Em =

-0.1408 + 0.3706i

т.е. имеем комплексное значение рассогласования .

Для оценки амплитудного значения ошибки следует перейти к модульному соотношению для :

.

В среде MatLab это осуществляется с помощью функции абсолютного значения abs:

>> Em=abs(Em)

Em =

0.3964

Полученное значение сравнивается с допустимой величиной ошибки слежения е_д, приведенной в табл.2.2 и делается соответствующий вывод. Пусть в нашем случае ошибка системы оказалась значительтно больше допустимой е_д = 25 угл.мин. = 0.0073рад, т.е. точность работы исходной САУ не удовлетворяет техническому заданию.