Министерство науки и образования РФ
Федеральное государственное бюджетное образовательное
Учреждение высшего образования
«Владимирский государственный университет им. А.Г. и Н.Г. Столетовых»
Лабораторная работа № 2-2
Определение коэффициента вязкости жидкости
И числа Рейнольдса методом падающего
В жидкостИ шарика
Выполнил:
Студент гр. ЗСу-218
К работе допущен
Работу выполнил
Работу сдал
Владимир 2019
Цель работы: исследование характера движения тела в вязкой жидкости.
Оборудование: длинный цилиндрический сосуд с исследуемой жидкостью и с двумя кольцевыми метками, набор шариков, микрометр, секундомер, линейка, термометр.
Введение
Силы, действующие на движущееся в жидкости тело, в значительной степени зависят от свойств жидкости. При безотрывном плавном обтекании тела идеальной жидкостью сила лобового сопротивления равна нулю ("парадокс" Даламбера). Обтекание тела вязкой жидкостью приводит к возникновению пограничного слоя, в котором влияние сил вязкости заметно, отрыву потока за телом и колебаниям потока из–за вихреобразования. В общем случае сила лобового сопротивления такого обтекания обусловлена: 1) касательными силами вязкости к поверхности тела; 2) перепадом давлений из–за отрыва потока; 3) колебаниями давления вследствие вихреобразования за телом. Какая из составляющих дает наибольший вклад в величину силы лобового сопротивления, в первую очередь, определяется значением критерия подобия числом Рейнольдса 
, где 
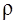– плотность жидкости; 
– характерная скорость потока; 
– характерный размер; 
– коэффициент вязкости жидкости. При малых скоростях потока жидкости, а следовательно, при малых числах Рейнольдса, главную роль играют силы вязкого трения. Стокс показал, что при движении тела в форме шара в вязкой жидкости вдали от стенок сосуда и поверхностей других тел сила лобового сопротивления Fc имеет вид
, (1)
где r – радиус шара. Формула Стокса (1) применима при условии Re <<1. Как видно из выражения (1), медленное движение тела в вязкой жидкости может быть использовано для определения величины коэффициента вязкости жидкости. Это осуществляется в установке, представленной на рисунке.
В широкий вертикально расположенный сосуд налита исследуемая жидкость. На сосуде сделаны по объему жидкости две горизонтальные метки, расстояние между которыми l. Метки достаточно далеко отстоят от дна и верхней кромки жидкости. В сосуд опускают металлический шарик массой m и плотностью ρМ с начальной скоростью, равной нулю. Как видно из рисунка, на шарик действуют три силы: сила тяжести, сила лобового сопротивления вязкой жидкости F 1 и выталкивающая сила Архимеда F. На начальном участке движение шарика ускоренное. Но так как с увеличением скорости растет сила лобового сопротивления, вскоре сумма всех сил, действующих на шарик, будет равна нулю, и шарик будет падать с постоянной скоростью. Метками и выделяется участок длины l, на котором шарик движется равномерно. Проекция суммы всех сил на вертикальную ось дает выражение
,
где 
, 
, 
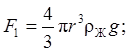
uo – скорость равномерного перемещения шарика;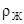 
– плотность жидкости.
Таким образом,
.
Отсюда получается выражение для коэффициента вязкости жидкости
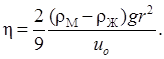
Если учесть, что 
, где 
– время равномерного перемещения шарика между метками, то окончательное выражение для вязкости
Условие применимости формулы (2) – Re<< 1 (см. выше). Это накладывает ограничения на размеры падающего шарика
(3)
если пренебречь архимедовой силой.
Порядок выполнения работы
1. Выбрать из наборов шаров известной плотности один и измерить его диаметр несколько раз (плотность стали – 7,8·103 кг/м3, плотность свинца – 11,3·103 кг/м3).
2. Установить метки на стеклянном сосуде достаточно далеко от края жидкости и дна. Измерить расстояние между метками.
3. Опустить шарик в жидкость известной плотности. При пролете шарика мимо верхней метки включить секундомер. При пролете шарика мимо нижней метки выключить секундомер. По разности показаний секундомера вычислить время τ. (Плотность касторового масла – 9,7·102кг/м3, плотность глицерина – 1,26·103 кг/м3).
4. Выполнить пп. 1 – 3 несколько раз.
5. Рассчитать по полученным данным среднее значение вязкости жидкости и числа Рейнольдса, вычислить погрешность измерений.
6. Сопоставить полученные результаты и неравенство (3), проверить справедливость применения формулы (2).
Дополнительное задание
Исследовать зависимость скорости движения шарика в жидкости от его диаметра. Предположив степенную зависимость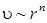 
,определить показатель степени n.
Контрольные вопросы
1. Вывести неравенство (3) из условия, что Re<< 1 и архимедова сила пренебрежимо мала.
2. Какие силы действуют на шарик, падающий в жидкость?
3. Чем обусловлено возникновение силы лобового сопротивления в вязкой жидкости: а) при малых скоростях движения шарика; б) высоких скоростях движения шарика?
4. Почему падение шарика в жидкость сначала ускоренное, затем становится равномерным?
5. Почему верхняя метка должна быть ниже уровня жидкости, а нижняя выше дна?
Список рекомендуемой литературы
1. Стрелков С.П. Механика. – М.: Наука, 1965. § 112. – 528 с.
2. Сивухин Д.В. Общий курс физики: В 5 т. – Т. 1. Механика. – М.: Наука, 1979. §§ 100, 101. – 519 с.
3. Савельев И.В. Курс общей физики: В 3 т. – Т. 1, – М.: Наука, 1977. § 78. – 352 с.