Министерство образования и науки Украины
Севастопольский национальный технический университет
Кафедра Автомобильного транспорта
КОНТРОЛЬНАЯ РАБОТА
АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ СИСТЕМАМИ АВТОМОБИЛЯ
Специальности 07.09.0258
«Автомобили и автомобильное хозяйство»
Выполнил: ст. гр. АВ-51з Калашников
Проверил: доц. Долгин. В.П.
Севастополь
ЗАДАНИЕ
Для подвески автомобиля указанной модели (выбрать в соответствии с вариантом)
Построить переходную h(t) (исследование подвески во временной области) и
2. частотные характеристики (исследование подвески в частотной области) A(w), F(w), Jm(w), Re(w), Jm(Re(w)) в диапазоне частот от Wmin=Wr/10 рад/с до Wmax=Wr*10 рад/с.
ЧАСТОТНЫЕ И ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ
ПОДВЕСКИ АВТОМОБИЛЯ МОДЕЛИ
Ст. гр. АВ-51з Калашников


Рисунок 1.1 – Кинематические схемы подвески автомобиля
Обозначения:
W - передаточная функция,
R(w)- вещественная частотная характеристика,
M(w)- мнимая частотная характеристика,
A(w)- амплитудная частотная характеристика,
F(w)- фазовая частотная характеристика,
ПАРАМЕТРЫПЕРЕДАТОЧНОЙ ФУНКЦИИ
W = b0/(a0+a1*p+a2*p^2);
a0 = c:a1:=L:a2:=m:b0:=c:
Yu = x*limit(W,p=0);
ПАРАМЕТРЫПОДВЕСКИ
Ma– 10185 Масса автомобиля
Mg–5000Грузоподъемность
Kz– 0 Коэффициент загрузки
Dh– 0.1 Осадка под нагрузкой
xi– 0,5 Коэффициент демпфирования (комфортности, xi=0,3..0,8)
m = (Ma+Mg*Kz)/4;
c = evalf(Mg*9.81/Dh)/4;
L = 2*xi*c*sqrt(m/c);
ПЕРЕХОДНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
При вычислениях переходной характеристики звена операторным методом необходимо выполнить следующие действия.
Получить изображение X (p) по Лапласу входного сигнала X (t) в соответствии с определением
X (p) => L{ X (t) },
что в терминах математического пакета MAPLE with (inttrans) имеет вид
Lx:=laplace(X,t,p); (Lx = X (p), X = X (t)).
Найти изображение выходного сигнала Y (p) => X (p)* W (p).
Перейти от изображения по Лапласу выходного сигнала Y (p) к оригиналу Y (t) в соответствии с определением
Y (t) => L-1{ Y (p) },
что в терминах математического пакета MAPLE with (inttrans) имеет вид
Px:=invlaplace(Lx*W,p,t); (Px = X (t), W = W (p)).
Таблица – Переходные характеристики
| Аналитическое решение | ||
| Тип звена | Передаточная функция | Переходная характеристика [1, с.92],[2, c. 296] |
| Коебательное ξ < 1 | 

|     . .
|
| Апериодическое, ξ ≥ 1 |  
|  ; ;  ; ;  ; ;  ; ;  ; ;  . .
|
РЕШЕНИЕ
1. Исследование во временной области
> # Блок 1
restart;
with(stats):
with(inttrans):
№:=051355; # НОМЕР ЗАЧЕТНОЙ КНИЖКИ
randomize(№); # ВАРИАНТ ЗАДАНИЯ
N:=10:
t1:=time():
№=051355
> # Блок 2
# Передаточная функция
W:= b0/(a0+a1*p+a2*p^2);
a0:= c:a1:=L:a2:=m:b0:=c:
Yu:=x*limit(W,p=0);


> # Блок 3
# ПАРАМЕТРЫПОДВЕСКИ
Ma:=6135: # Масса автомобиля
Mg:=5000: # Грузоподъемность
Kz:=0; # Коэффициент загрузки
Dh:=0.10: # Осадка под нагрузкой
xi:=0.5: # Коэффициент демпфирования (xi=0,3..0,8)
m:= evalf((Ma+Mg*Kz)/4);
c:= evalf(Mg*9.81/Dh)/4;
#c:=c/2;
xi:=xi/1.5:
L:= 2*xi*sqrt(m*c);
T:=sqrt(m/c);





> # Блок 4
# Переходная характеристика
x:=1: # Скачок
Lx:=laplace(x,t,p); # Изображение сигнала
Px:=invlaplace(Lx*W,p,t); # Обратное преобразование Лапласа


> # Блк 5
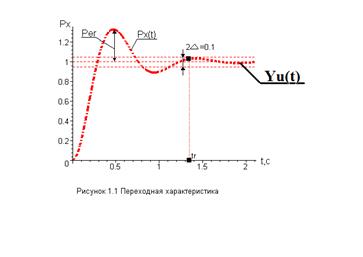
# Графики переходной характеристики
t0:=15*T: # Время переходного процесса
tr:=1.35: # Время регулирования
G1:=plot([tr,J,J=0..subs(t=tr,Px)],linestyle=2):
G2:=plot(Px,t=0..t0,linestyle=4,thickness=4):
G3:=plot(Yu*1.05,t=0..t0,linestyle=4):
G4:=plot(Yu*0.95,t=0..t0,linestyle=4):
G5:=plot(Yu,t=0..t0,linestyle=4):
plots[display]({G1,G2,G3,G4,G5},title="Переходная характеристика");
# Блок 6
# Перерегулирование
Max:=maximize(Px,t=0..t0):
Kz:=Kz;
c:=c;
L:=L;
Per:=Max-x;
tr:=tr;





2. Частотные характеристики
> # Блок 6
# ОПИСАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
p:=I*w:
R(w):=evalc(Re(W));
M(w):=evalc(Im(W));
A(w):=abs(W);
F(w):=argument(W);




> # Блок 7
# ДИАПАЗОН ЧАСТОТ
T:=sqrt(a2/a0):
Wr:=evalf(sqrt(1-2*xi^2)/T); # [1,стр.117]
Wmax:=Wr*10; Wmin:=Wr*.1;



> # Блок 8
# ГОДОГРАФ
G:=plot([R(w),M(w), w=0..Wmax],color=red,style=line,thickness=3):
plots[display]({G},title=`ГОДОГРАФ `);

> # Блок 9
# ОПИСАНИЕ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
G1:=plot([log10(w),R(w), w=Wmin..Wmax],
color=red,linestyle=4,thickness=3,legend="R(w)"): # ВЧХ
G2:=plot([log10(w),M(w), w=Wmin..Wmax],
color=blue,style=line,thickness=3,legend="M(w)"): # МЧХ
G3:=plot([log10(w),A(w), w=Wmin..Wmax],
color=red,linestyle=4,thickness=3,legend="A(w)"): # АЧХ
G4:=plot([log10(w),F(w), w=Wmin..Wmax],
color=black,style=line,thickness=3,legend="F(w)"): # ФЧХ
> # Блок 10
# ГРАФИКИ ЛАЧХ [A(w)] и ЛФЧХ [F(w)]
g:=1.01:
Am:=evalf(1/(xi*sqrt(1-xi^2)*2)); # [1, с.117]
G5:=plot([log10(w),Am,w=Wr/g..Wr*g],style=point,
symbol=circle,symbolsize=15,legend="Am"):
G6:=plot([log10(Wr),J,J=0..Am],linestyle=2,legend="Wm"):
G7:=plot([log10(w),-Pi, w=Wmin..Wmax],linestyle=4,legend="Pi"):
plots[display]({G3,G4,G5,G6,G7},title=`ЛАЧХ и ЛФЧХ`);


Рисунок 1.3 - Графики ЛАЧХ и ЛФЧХ
# Блок 11
# ГРАФИКИ ЛВЧХ [R(w)] и ЛМЧХ [M(w)]
plots[display]({G1,G2},title=`ЛВЧХ и ЛМЧХ`);
Kz:=Kz;
L:=L;
c:=c;
Wr:=Wr;

Рисунок 1.4 – Графики ЛВЧХ и ЛМЧХ




Выводы: Для указанных параметров системы переходный процесс имеет колебательный характер. Время окончания переходного процесса на уровне 5% - менее 3,4с.
Перерегулирование составляет величину менее 0,5
Приложение
| Выпускается Московским автозаводом имени Лихачева с 1986г. Кузов - деревянная платформа армейского типа с откидным задним бортом, в решетках боковых бортов вмонтированы откидные скамейки на 16 посадочных мест, имеется средняя съемная скамейка на 8 мест, предусмотрена установка дуг и тента. Кабина - трехместная, расположена за двигателем, сиденье водителя - регулируемое по длине, высоте, наклону подушки и спинки. Основной прицеп СМЗ-8325 (армейский). | 
| |
Модификация автомобиля:
- ЗИЛ-131НА - автомобиль с неэкранированным и негерметизированным электрооборудованием;
- ЗИЛ-131НС и ЗИЛ-131НАС - исполнение ХЛ для холодного климата (до минус 60°С).
По заказу автомобили ЗИЛ-131Н могут выпускаться в виде шасси без платформы для монтажа различных кузовов и установок.
С 1966 до 1986 гг. выпускался автомобиль ЗИЛ-131.
|