Урок: Преобразование выражений с корнями (внесение множителя под знак корня)
Повторение определения и основных свойств квадратного корня
Начнем урок с повторения теории.
Определение. Квадратным корнем из неотрицательного числа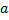 
называется такое неотрицательное число 
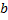, квадрат которого равен .
.
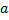Из определения следует тождество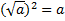 
при 
.
При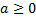мер 1. Вычислите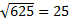 
, т. к. 
.
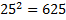Пример 2. Решите уравнение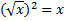 
Решение. Уравнение может показаться очевидным и выполненным всегда при всех значениях переменной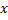 
. Действительно, мы уже знакомы с тождеством, которое представляет собой это уравнение, однако, важно помнить, что оно выполнено при 
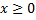, что и будет являться решением уравнения. Это тот случай, в котором решением уравнения может являться не одно или несколько чисел, как мы привыкли, а целая числовая полуось.
Ответ. .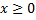
Основные свойства квадратного корня:
а)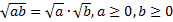 
б)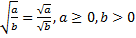 
в)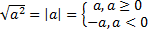 
Рассмотрим две важнейшие типовые задачи урока, на методе решения которых будет базироваться подход к другим подобным задачам.
Две типовых задачи на внесение множителя под квадратный корень
Пример 3. Внесите множитель под знак корня: а)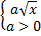 
, б)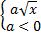 
.
Решение. Задачи отличаются только знаком выражения, которое является множителем перед корнем, но это принципиальный аспект дальнейшего решения.
а) Внесение положительного множителя под знак корня. Если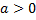 
, то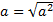 
, тогда 
.
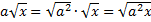б) Внесение отрицательного множителя под знак корня. Если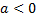 
, то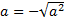 
(т. к. 
), тогда 
.
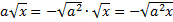Ответ.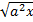 
; 
.
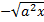Как видно из приведенного примера, знак вносимого под корень выражения важен, и если он отрицательный, то перед корнем после внесения множителя должен остаться минус, в случае внесения положительного множителя, значение выражения остается положительным.
Когда нам известны два принципиальных подхода к решению задач, можем перейти к различным примерам.
Различные примеры на внесение множителя под квадратный корень
Пример 4. Внесите множитель под знак корня: а)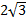 
, б) 
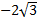, в)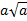 
.
Решение. а) Т. к. множитель перед корнем положительный, то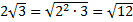 
.
б) Т. к. множитель перед корнем отрицательный, то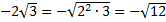 
.
в) В этой задаче может показаться, что решение имеет различные варианты, т. к. знак выражения перед корнем не известен, но следует заметить, что такое же выражение находится и под знаком корня, т. е. оно неотрицательно по определению квадратного корня (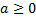). Имеем вариант для внесения неотрицательного числа 
.
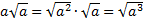Ответ.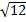 
; 
; 
.
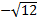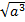Пример 5. Внесите множитель под знак корня и упростите: а)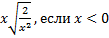 
, б) 
.
Решение. Задачи похожи, однако, отличаются знаками вносимых под корень множителей, подход к решению нам уже известен, применим его.
а)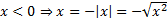 
, тогда 
.
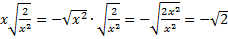б)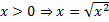 
, тогда 
.
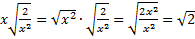Ответ.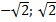 
.
Пример 6. Внесите множитель под знак корня и упростите: а)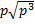 
, б) 
.
Решение. а) По определению квадратного корня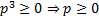 
, т. к. если произведение трех одинаковых чисел неотрицательно, то и эти числа неотрицательны, тогда вносим под корень неотрицательное число: 
.
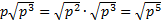б) По определению квадратного корня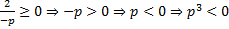 
, тогда вносим под корень отрицательное число: 
.
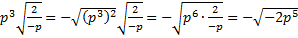Ответ.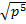 
; 
.
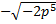На следующем уроке рассмотрим более сложные задачи на преобразования выражений с корнями, в которых нам понадобятся знания обо всех основных свойствах квадратного корня.
1. Внесите множитель под знак корня: а)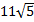 
, б) 
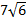, в)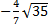 
.
2. Внесите множитель под знак корня, если известно, что 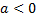: а) 
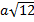, б)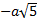 
.
3. Расположите в порядке возрастания числа: а)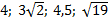 
, б)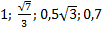 
.