Этап 1. Определение частных показателей (критериев) средств защиты и вычисление их относительных значений.
На первом этапе вычисления определяют относительное значение одного и того же частного показателя для различных средств защиты информации. Каждое значение частного показателя средств защиты информации делят на наилучшее и получают относительное значение частного показателя. Аналогично вычисляют относительные оценки для всех частных показателей средств защиты информации (СЗИ) и составляют таблицу.
Этап 2. Вычисление весовых коэффициентов критериев на основе применения метода анализа иерархий.
Необходимо осуществить заполнение квадратной матрицы парных сравнений критериев по следующему правилу (табл. 3).
Матрицы критериев попарных сравнений обладают свойством обратной симметрии, т.е.:
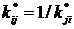, (5)
где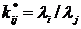 
; 
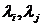- экспертные оценки элементов 
; i,j – индексы относятся к строке и столбцу.
Таблица 3 - Матрица парных сравнений
| К1 | К2 | … | Кn | |
| К1 |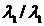 
| 
| … | 
|
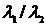
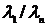
| К2 |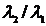 
| 
| … | 
|
| … | … | … | … | … |
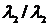
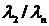
| Кn |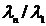 
| 
| … | 
|
Результаты парных сравнений (5) отражают превосходство одного критерия над другим, при этом рекомендуется использовать шкалу относительной важности (табл.4).
Таблица 4 – Шкала относительной важности
| Интенсивность относительной важности | Определение |
| Равная важность | |
| Умеренное превосходство одного над другим | |
| Существенное или сильное превосходство | |
| Значительное превосходство | |
| Очень сильное превосходство | |
| 2, 4, 6, 8 | Промежуточные решения между двумя соседними суждениями |
| Обратные величины приведенных выше чисел | Если при сравнении одного элемента с другим получено одно из вышеуказанных чисел (например, 7), то при сравнении второго элемента с первым получим обратную величину (т.е. 1/7) |
В результате экспертного оценивания по правилу (5) была построена таблица 5, вычислены оценки компонентов собственного вектора, а также получены нормализованные результаты оценки вектора приоритетов.
|
|
Для получения оценки вектора приоритетов, необходимо сначала вычислить компоненты собственного вектора по строкам матрицы. Процедура определения собственных векторов состоит из перемножения n-элементов в строке матрицы и извлечения корня n-й степени из перемноженных элементов (т.е. геометрической средней по строкам матрицы). Полученный таким образом столбец чисел нормализуется делением каждого числа на сумму элементов собственного вектора. Нормализованный столбец чисел и будет являться вектором приоритетов (см. табл. 5).
Вычислим значение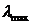 
из данных таблицы 3 по следующему выражению:
,
где А – матрица парных сравнений;
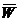– нормализованный собственный вектор (вектор приоритетов).
Величина 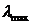определяется путем вычисления вектора столбца 
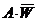с последующим суммированием его элементов
Мера согласованности относительных оценок может быть выражена с помощью индекса согласованности. Согласованность локальных приоритетов проверим путем вычисления индекса согласованности (ИС) и отношения согласованности (ОС). Для индекса согласованности имеем
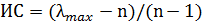, (6)
где n – число сравниваемых элементов матрицы;
– максимальное собственное значение рассматриваемой матрицы суждений.
Отношение согласованности получаем путем деления значения ИС на число, соответствующее случайной согласованности матрицы того же порядка (см. табл. 6).
|
|
Величина ОС должна быть порядка 10% или менее, чтобы быть приемлемой. В некоторых случаях допускается 20%, но не более. Если ОС выходит за эти пределы, то необходимо вновь исследовать задачу и проверить все суждения.
Таблица 6 – Соответствие порядка матрицы и среднего значения случайного индекса
| Размер матрицы | ||||||||||
| Случайная согласованность | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
Контрольный пример
(выполняется согласно этапам МАИ совместно на занятии)
Решение:
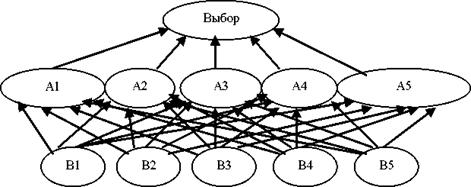
1. Строим иерархию (рис.5.1):
|
Рис.5.1.Иерархия
Где:
А1, А2,..., А5 - критерии Делопроизводство, Внешний вид, Английский язык, Знание компьютера, Умение разговаривать по телефону.
В1, В2,., В5 - альтернативы Ольга, Елена, Светлана, Г алина, Жанна.
2. Строим матрицу парных сравнений для критериев и рассчитываем оценки. Для этого строим матрицу размерностью 5х5 (по числу критериев) и подпишем строки и столбцы наименованиями сравниваемых критериев.
Заполняем табл.5.2. Для этого попарно сравниваем критерий из строки с критерием из столбца по отношению к цели - выбору секретаря. Значения из шкалы относительной важности (табл. 5.1) вписываем в ячейки, образованные пересечением соответствующей строки и столбца.
Таблица 5.2
|
|
|
Сначала определяем оценки компонент собственного вектора. Так для критерия "Внешность" это будет:
(1 x 1/5 x 1/5 x 1/6 x 1/6)1/5 = 0,25654
Получив сумму оценок собственных векторов (= 6,39069), вычисляем нормализованные оценки вектора приоритета для каждого критерия, разделив значение оценки собственного вектора на эту сумму. Для того же критерия "Внешность" имеем:
0,25654 / 6,39069= 0,04014 Результаты заносим в табл. 5.3.
Таблица 5.3
Рассчитаем Lmax (табл. 5.4):
|
Таблица 5.4
|
Сравнивая нормализованные оценки вектора приоритета можно сделать вывод, что наибольшее значение при выборе секретаря придается критерию "Знание компьютера".
Необходимо проверить, насколько суждения были непротиворечивыми при составлении матрицы парных сравнений критериев. Для этого необходимо рассчитать отношение согласованности и индекс согласованности для этой матрицы.
ОС = Ис/ число, соответствующее случайной согласованности матрицы пятого порядка, равного 1,12. Отношение согласованности должно быть меньше 10.
Ис = (Lmax-n)/(n-1)
Ис = (5,2268-5)/(5-1) = 0,0567
ОС = 0,0567/1,12 = 5,06%
Величина ОС < 10% значит пересматривать свои суждения нет нужды
3. Строим матрицу парных сравнений для альтернатив (девушек) по каждому критерию и рассчитываем оценки. Для этого строим матрицы размерностью 5х5 (по числу альтернатив) и подпишем строки и столбцы наименованиями альтернатив.
Для этого попарно сравниваем альтернативу из строки с альтернативой из столбца по каждому критерию отдельно. Значения из шкалы относительной важности (табл. 5.1) вписываем в ячейки, образованные пересечением соответствующей строки и столбца.
Затем определяем оценки компонент собственного вектора для каждой матрицы. Получив сумму оценок собственных векторов, вычисляем нормализованные оценки вектора приоритета для каждой альтернативы по каждому критерию.
Затем для каждой матрицы рассчитываем отношение согласованности и индекс согласованности. Расчеты приведены в табл. 5.5 - табл. 5.14.
Критерий «Внешность»
Таблица 5.5
| Ольга | Елена | Светлана | Галина | Жанна | Оценки компонент собственного вектора | Нормализо ванные оценки вектора приоритета | |
| Ольга | 1/5 | 1/4 | 1,084472 | 0,150519 | |||
| Елена | 3,200869 | 0,444264 | |||||
| Светлана | 1/5 | 1/6 | 1/5 | 0,457305 | 0,063472 | ||
| Галина | 1/6 | 1/7 | 1/3 | 1/5 | 0,275507 | 0,038239 | |
| Жанна | 1/2 | 2,186724 | 0,303506 | ||||
| Сумма | 7,204876 |
Рассчитаем Lmax:
Таблица 5.6
|
Ис = (5,35485-5)/(5-1) = 0,0879 ОС = 0,0879/1,12 = 7,85%
Величина ОС < 10% значит пересматривать свои суждения нет нужды
Критерий «Знание языка»
Таблица 5.7
Рассчитаем Lmax:
|
Таблица 5.8
|
Ис = (5,24665-5)/(5-1) = 0,0617
ОС =0,0617 /1,12 = 5,51% Величина ОС < 10% значит пересматривать свои суждения нет нужды