Анализ таблиц сопряженности размера 2X2
Простейшая задача о взаимосвязи возникает тогда, когда имеются два признака, каждый из которых принимает два значения.

Основы корреляционного анализа
представляющая собой среднее из абсолютных величин отклонений отдельных значений признака от среднего значения признака:


Среднее линейное и среднее квадратическое отклонение являются мерой абсолютной колебаемости признака и всегда выражаются в тех же единицах измерения, в которых выражен изучаемый признак. Это не позволяет сопоставлять между собой средние отклонения различных признаков (в случае разных единиц измерения) в одной и той же совокупности, а также одного и того же признака в разных совокупностях с различными средними. Чтобы иметь такую возможность, средние отклонения часто выражаются в процентах к среднему арифметическому, т.е. в виде относительных величин.
Отношение среднего линейного или среднего квадратического отклонения к среднему арифметическому называется коэффициентом вариации.
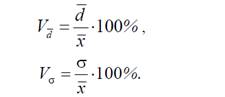
Очевидно, что тот из рядов имеет большее рассеяние, у которого коэффициент вариации больше.
Анализ таблиц сопряженности размера 2X2
Простейшая задача о взаимосвязи возникает тогда, когда имеются два признака, каждый из которых принимает два значения.

Основы корреляционного анализа
Закономерности при проявлении социально-экономических и политических процессов складываются под влиянием множества причин, которые действуют одновременно и взаимосвязано. Изучением взаимосвязанности между несколькими величинами в основном занимается корреляционный анализ.
Наиболее широко известной мерой связи служит коэффициент корреляции Пирсона (rхy)

Коэффициент корреляции может изменяться от -1 до +1. Если он равен 0, то связь между признаками отсутствует.
После вычисления коэффициента корреляции возникает вопрос, насколько показателен этот коэффициент и не обусловлена ли зависимость, которую он фиксирует случайными отклонениями. Иначе говоря, необходимо проверить гипотезу о том, что полученное значение коэффициента корреляции значимо отличается от 0. Если гипотеза H0 (rху =0) будет отвергнута, говорят,
что величина коэффициента корреляции статистически значима, т.е. эта величина не обусловлена случайностью, при уровне значимости  .
.
Для случая, когда n < 50, применяется критерий Стьюдента (t):

Коэффициенты ранговой корреляции (Спирмена, Кендалла) используются для измерения взаимосвязи между качественными признаками, значения которых могут быть упорядочены или проранжированы по степени убывания или нарастания данного качества у исследуемых объектов. Наиболее простым с точки зрения процедуры вычисления является коэффициент ранговой корреляции Спирмена (rs):
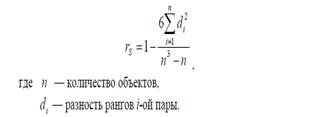
Величина rs также как и коэффициент корреляции Пирсона изменяется от -1 до +1. Значимость коэффициента корреляции Спирмена для n <100 определяется по таблице критических значений коэффициента rs, зависящего от задаваемого уровня значимости а и n. Если n >100, то критические значения находятся по таблице значений критических точек стандартного нормального распределения. Наблюдаемые значения критерия вычисляются по формуле

Коэффициенты ранговой корреляции используются как меры взаимозависимости между рядами рангов, а не как меры связи между значениями самих переменных.