Запишите конспект в тетрадь
Понятие вектора
Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто векторами. Векторами являются, например, скорость, ускорение, сила.
Геометрически векторы изображаются направленными отрезками. Направленный отрезок, для которого указано какой из его концов считается началом, а какой концом называется вектором. Вектор характеризуется следующими элементами: 1) начальной точкой (точкой приложения); 2)направлением; 3) длиной («модулем вектора»).
Если начало вектора — точка А, а его конец — точка В, то вектор обозначается  или или  .
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.
Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления. Обозначается: .
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.
Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления. Обозначается: 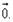 .
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора .
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора  . Обозначается . Обозначается  . .
|
 векторы
векторы 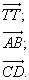


|
Два вектора называются равными, если они совмещаются параллельным переносом. АВСD — параллелограмм, 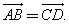
|

|
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если векторы  и и  коллинеарны и их лучи сонаправлены, то векторы коллинеарны и их лучи сонаправлены, то векторы  и и  называются сонаправленными. Обозначаются называются сонаправленными. Обозначаются  . Если векторы . Если векторы  и и  коллинеарны, а их лучи не являются сонаправленными, то векторы коллинеарны, а их лучи не являются сонаправленными, то векторы  и и  называются противоположно правленными. Обозначаются называются противоположно правленными. Обозначаются 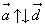 . Нулевой вектор условились считать сонаправленным с любым вектором. . Нулевой вектор условились считать сонаправленным с любым вектором.
|
 коллинеарные векторы:
коллинеарные векторы: 
|
Свойство коллинеарных векторов
Если векторы  и и  коллинеарны и коллинеарны и  , то существует число k такое, что , то существует число k такое, что 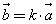 . причем если k > 0, то векторы . причем если k > 0, то векторы  и и  сонаправленные, если k < 0, то противоположно направленные. сонаправленные, если k < 0, то противоположно направленные.
| |
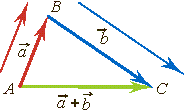
Правило треугольника Каковы бы ни были точки А, В, С, имеет место векторное равенство:

| 
|
Рисунки иллюстрируют сложение коллинеарных векторов с помощью параллельного переноса.

| Если при сложении векторов  и и  по правилу треугольника точку А заменить другой точкой А 1, то вектор по правилу треугольника точку А заменить другой точкой А 1, то вектор  заменится равным ему вектором заменится равным ему вектором  . .

|
Правило параллелограмма
Если векторы  и и  неколлинеарны, их можно отложить от одной точки, достроив затем параллелограмм. Диагональ параллелограмма есть сумма двух векторов неколлинеарны, их можно отложить от одной точки, достроив затем параллелограмм. Диагональ параллелограмма есть сумма двух векторов  и и  . .
| 
|
Свойства сложения векторов
Для любых векторов  заданных в пространстве, справедливы равенства
заданных в пространстве, справедливы равенства
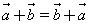
| Переместительный закон |

| Сочетательный закон |
Правило многоугольника применяется, если нужно найти сумму трех или большего числа векторов. Сумма нескольких векторов не зависит от того, в каком порядке они складываются. От произвольной точки О отложен вектор 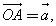 затем от точки А отложен вектор затем от точки А отложен вектор  и, наконец, от точки В отложен вектор и, наконец, от точки В отложен вектор  В результате получается вектор В результате получается вектор 
|
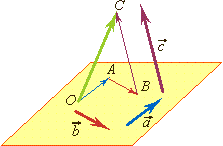
| ||
Умножение вектора на число
Произведением ненулевого вектора  на число k называется такой вектор, на число k называется такой вектор,  , длина которого равна, , длина которого равна, 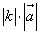 , причем векторы , причем векторы  и и  сонаправлены при сонаправлены при  и противоположно направлены при k < 0. Произведением нулевого вектора на любое число считается нулевой вектор. и противоположно направлены при k < 0. Произведением нулевого вектора на любое число считается нулевой вектор.
|


