Динамические свойства САУ определяются как свойствами самого объекта управления, так и регулятора. Объект управления – это, как правило, неизменяемая часть САУ, характеристики которой определяются конструктивными и технологическими особенностями конкретного агрегата. Если объект управления представлен набором типовых динамических звеньев, соединенных определенным образом, то используя правила преобразования структурнвх схем, необходимо свести их к одному, более сложному звену.
Пример 2. Структурная схема САУ имеет вид, представленный на рисунке l, a. Определить ее передаточную функцию.
Решение. Заменим сначала группу параллельно соединенных звеньев W3(P) и W4(P) одним более сложным звеном WI(P) (рисунок 1, а). Передаточная функция этого звена будет равна сумме передаточных функций отдельных звеньев:
 .
.
В результате такого преобразования получаем упрощенную схему (рисунок 1, б). В качестве дальнейшего этапа преобразования введем вместо цепочки последовательно соединенных звеньев W2(P), WI(P) и W5(P) одно звено WII(P) (рисунок 1, в) с передаточной функцией, равной их произведению:
 .
.
После этого звено WII(P), охваченное отрицательной обратной связью W6(P), заменяем новым звеном WIII(P) (рисунок 1, г):
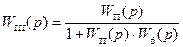 .
.
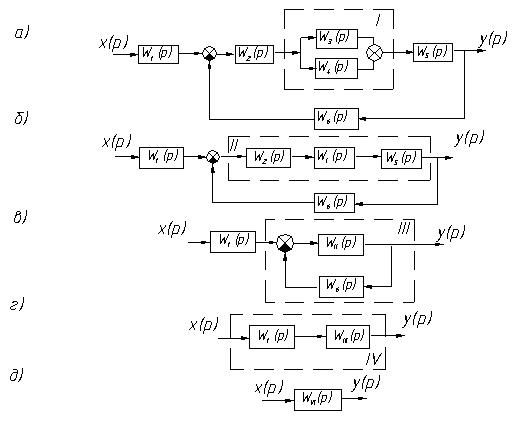
а – параллельное соединение звеньев; б – последовательное соединение;
в – встречно-параллельное соединение; г – последовательное соединение;
д – эквивалентное звено
Рисунок 1 – Структурная схема САУ
Наконец, представляем всю систему в виде одного эквивалентного звена WIV(P) (рисунок 1, д), передаточная функция которого:
 .
.
Любая САУ содержит объект регулирования и регулятор. Схема взаимодействия объекта и регулятора, описанных передаточными функциями Wo(p) и WR(p), при реализации принципа управления по отклонению, представлена на рисунке 2.

Рисунок 2 – Структурная схема объекта с регулятором
В качестве автоматического регулятора чаще всего применяются непрерывные П, И, ПИ, ПД и ПИД регуляторы. При изучении законов регулирования следует обратить внимание на параметры настройки регуляторов, т. е. на те величины, которым при настройке регуляторов необходимо придавать определенные числовые значения с целью достижения желаемых результатов процесса регулирования. Этими параметрами являются коэффициенты дифференциальных уравнений k, k1, TИ и ТД.
Главными факторами, определяющими применимость того или иного типа регулятора, являются динамические характеристики объекта регулирований К, Т, t и требуемый характер переходного процесса.
Пример 3. На объекте из примера 2, описанном последовательно соединенными апериодическими звеньями с передаточными функциями WА(p) и WВ(p)
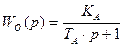 ×
×  ,
,
установлен регулятор из примера 1. С помощью критерия Гурвица определить допустимое по условиям устойчивости системы значение параметра настройки регулятора kR.
Решение. Передаточная функция объекта с учетом того, что KA KB = k0 ,
 .
.
Передаточная функция регулятора

Тогда передаточная функция замкнутой САУ с регулятором имеет вид:
 .
.
Устойчивость
Понятие устойчивости является одним из основных понятий динамики САУ. Для устойчивости линейной САУ необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части. Это можно установить с помощью критериев устойчивости, не решая дифференциального уравнения. Существуют алгебраические (Рауса, Гурвица, Вышнеградского) и частотные (Михайлова, Найквиста) критерии устойчивости.
С помощью критериев устойчивости можно не только проверить САУ на устойчивость, но также определить области допустимого по условиям устойчивости изменения величины какого-либо параметра системы (например, параметра настройки регулятора ТИ - постоянной времени интегрирования). При этом предельным значением такого параметра будет то его значение, при котором критерии свидетельствуют о нахождении САУ на границе устойчивости.
Пример 4 - Для замкнутой САУ из примера 3 найти область существования параметра настройки регулятора, при котором САУ будет устойчива.
Решение. Из передаточной функции замкнутой САУ выделяем характеристическое уравнение (это знаменатель передаточной функции, приравненный нулю).
Характеристическое уравнение САУ имеет вид:
 = 0
= 0
Для определения области существования значений параметра настройки регулятора ТИ воспользуемся алгебраическим критерием устойчивости Гурвица. Он гласит, что система будет устойчива если все коэффициенты характеристического уравнения положительны, а определитель Гурвица больше нуля. Составление определителя Гурвица начинается со второго коэффициента, затем по диагонали выписываются последующие. Первый и последний коэффициенты выписываются в столбцы, соответственно вниз и вверх. Решая полученный определитель относительно ТИ, получаем область устойчивого существования САУ.
 > 0.
> 0.
Таким образом, САУ будет устойчива при  .
.
Контрольная работа
Задача
1) Определить передаточную функцию объекта регулирования, структурная схема которого приведена на рисунке 3. Каждый студент выбирает тот вариант, номер которого совпадает с последней цифрой его шифра.
Передаточные функции отдельных звеньев объекта представлены в таблице 2. Символ «0» обозначает, что данное звено в схеме отсутствует, обратные связи отрицательные. Структурные преобразования схемы объекта регулирования можно выполнить в соответствии с примером 2 раздельно по группам звеньев А и В. Эти группы характеризуют отдельные емкости объекта. Привести названия составляющих звеньев.
2) Используя критерий устойчивости Гурвица определить предельно допустимые по условиям устойчивости САР значения параметров настройки И-регулятора, указанного в примере 1, установленного на объекте регулирования, представленного на рисунке 3, при реализации принципа управления по отклонению. Схема его установки на объекте соответствует рисунку 2.

Рисунок 3 – Структурная схема объекта
Таблица 1 – Передаточные функции звеньев
| W(p) | Вариант | |||||||||
| W1(p) | 
| 
| 
| 
| 
| 
| ||||
| W2(p) | 
| 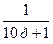
| 0,5 | 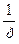
| 0,1 | 
| 
| |||
| W3(p) | 
| 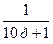
| 0,5 | 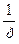
| 0,1 | 
| 
| |||
| W4(p) | 0.1 | 0.5 | 0.5 | 0,1 | ||||||
| W5(p) | 
| 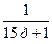
| 
| 0,1 | 
| |||||
| W6(p) | 
| 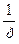
| 4/p | 
| 
| 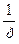
| 
| |||
| W7(p) | 
|
Список литературы
1 Н. Ф. Метлюк, Автоматика и автоматизация производственных процессов. - Минск: Выш. шк.,1985. - 301 с.
2 Ксеневич, И. П. Теория и проектирование автоматическиx систем / И. П. Ксеневич, В. П. Тарасик - М.: Машиностроение, 1996.- 480 с.