Тема: Признак перпендикулярности плоскостей.
Дата: 09.10.2020 г.
Группа: ПЦ-262
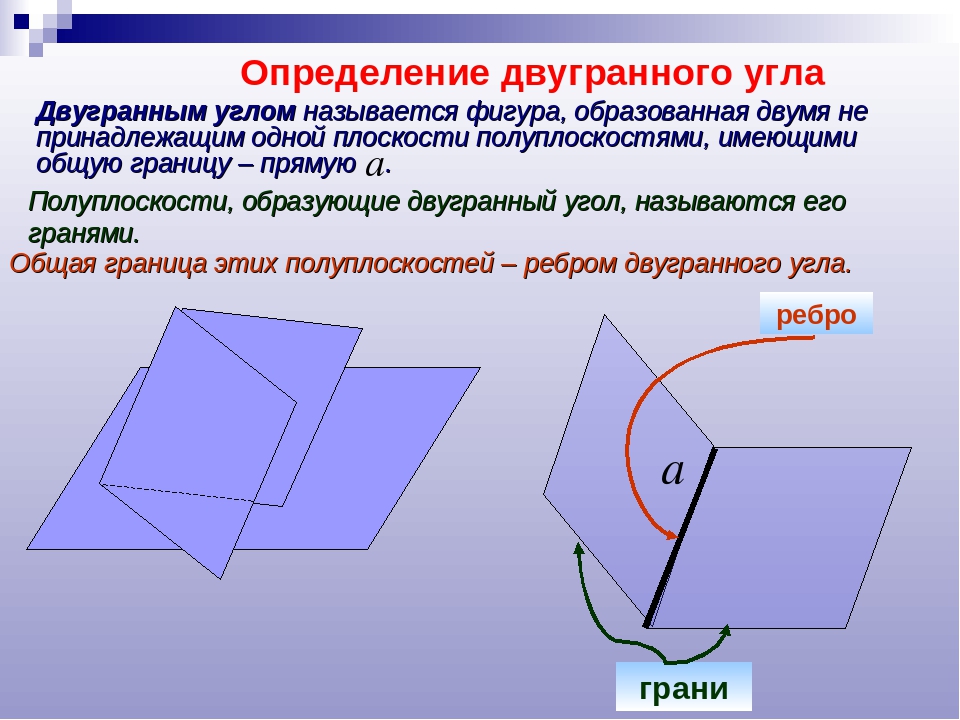
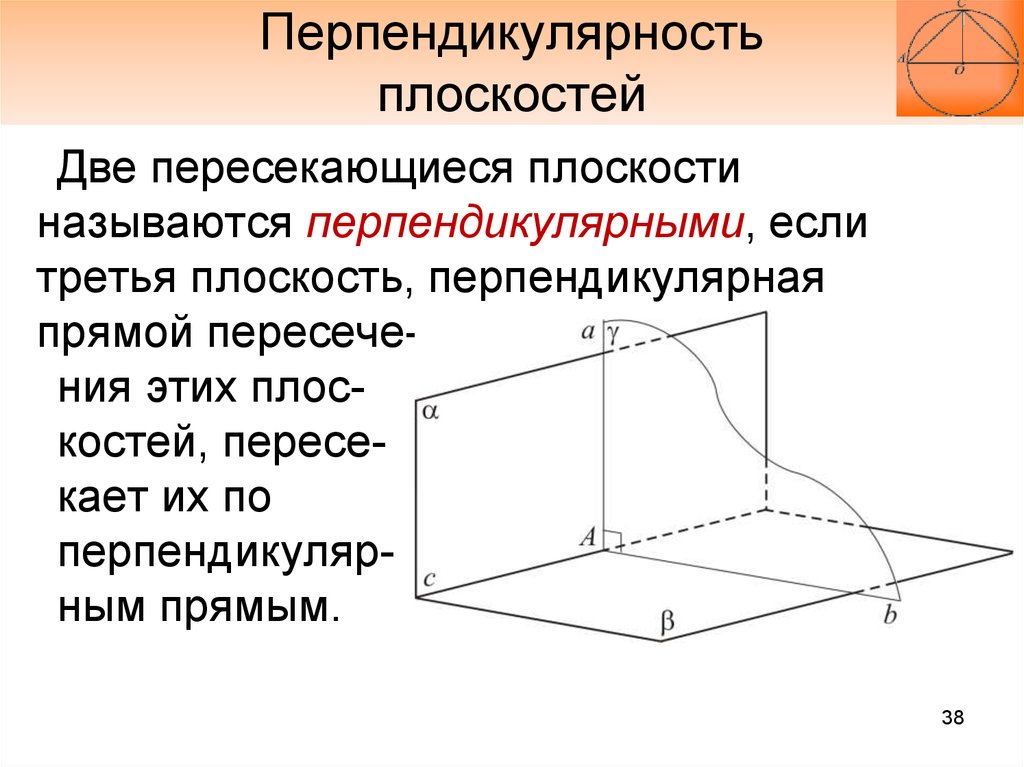
Студенты должны знать: определение двугранного угла, его виды, определение перпендикулярных плоскостей
Студенты должны уметь: применять теоремы при решении задач, графически изображать перпендикулярные плоскости
Актуализация знаний студентов
Изучение нового материала
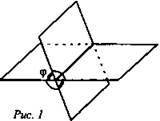
При пересечении двух плоскостей образуются четыре двугранных угла. Углом между пересекающимися плоскостями называется линейный угол φ этого двугранного угла, который 0° < φ ≤ 90° (рис. 1).
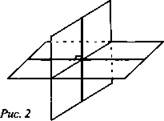
Если φ = 90°, то плоскости называются перпендикулярными (взаимно перпендикулярными) (рис. 2).
Вопрос: Приведите примеры взаимно перпендикулярных плоскостей.
(Плоскости стены и пола, стены и потолка комнаты).
Вопрос: Ясно, что в этих случаях каждый из четырех двугранных углов, образованных пересекающимися плоскостями, прямой (рис. 2). Рассмотрим признак перпендикулярности двух плоскостей.
Теорема: Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
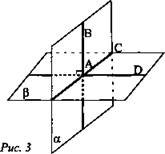
Дано: α, β, АВ лежит в плоскости α, АВ ⊥ β, АВ ∩ α = А (рис. 3). Доказать: α ⊥ β.
Доказательство: α ∩ β = АС, АВ ⊥ АС, так как АВ ⊥ β по условию. Проведем в плоскости βAD ⊥ AC. ∠BAD - линейный угол двугранного угла. Но ∠BAD = 90, так как ВА ⊥ β. Значит, α ⊥ β.
Теорема: Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Дано: α, β, АВ лежит в плоскости α, АВ ⊥ β, АВ ∩ α = А (рис. 3). Доказать: α ⊥ β.
|
|
Доказательство: α ∩ β = АС, АВ ⊥ АС, так как АВ ⊥ β по условию. Проведем в плоскости βAD ⊥ AC. ∠BAD - линейный угол двугранного угла. Но ∠BAD = 90°, так как ВА ⊥ β. Значит, α⊥ β.
Закрепление изученного материала.
При решении задач используются утверждения:
1. Плоскость, перпендикулярная к ребру двугранного угла, перпендикулярна к его граням (следствие).
2. Перпендикуляр, проведенный из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости (№ 178).
3. Из этой теоремы вытекает важное следствие:
Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
4.
Задача: №172
Дано: ΔАВС, ∠С = 90°, АС лежит в плоскости α, угол между плоскостями α и ABC равен 60°, АС = 5 см, АВ = 13 см (рис. 4). Найти: расстояние от точки В до плоскости α.
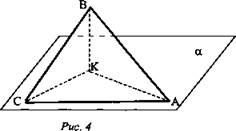
Решение: Построим ВК ⊥ α. Тогда КС - проекция ВС на эту плоскость. ВС ⊥ АС по условию, значит, по теореме о трех перпендикулярах, КС ⊥ АС. Отсюда следует, что ∠ВСК - линейный угол двугранного угла между плоскостью α и плоскостью треугольника, ∠ВСК = 60°. Из ΔВСА
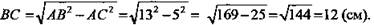по теореме Пифагора:
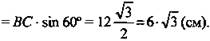
Из ΔВКС:
Ответ: 6√3 см.
№ 172
Дано: ΔАВС, ∠С = 90°, АС Îα, угол между плоскостями α и ABC равен 60°, АС = 5 см, АВ = 13 см (рис. 4). Найти: расстояние от точки В до плоскости α.
Решение: Построим ВК ⊥ α Þ КС - проекция ВС на эту плоскость. ВС ⊥ АС по условию, значит, по теореме о трех перпендикулярах, КС ⊥ АС Þ∠ВСК - линейный угол двугранного угла между плоскостью α и плоскостью треугольника, ∠ВСК = 60°.
|
|
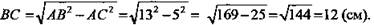Из ΔВСА:
Из ΔВКС: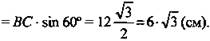
Ответ: 6√3 см.
Домашнее задание:
«Геометрия 10-11» А.В.Погорелов п. 20 стр.40, №59 (1,2,3)
Критерии оценивания:
1.Оценка «отлично» - выставляется обучающемуся, если правильно решены все задания, выполнены в полной мере, изложены логично.
1. Оценка «хорошо» - выставляется обучающемуся, если допущены незначительные погрешности в задании.
2. Оценка «удовлетворительно» - выставляется обучающемуся, если ответ на вопрос нелогичный, не полный.
3. Оценка «неудовлетворительно» - выставляется обучающемуся, если задания не решены.
ВНИМАНИЕ!!!
Уважаемые студенты, практическое задание необходимо выполнить в рабочей тетради (сфотографировать) или в формате Документа Word. Отправлять для проверки в личные сообщения на страницу ВКонтакте: https://vk.com/kolomiyetssg?z=photo95751036_324720501%2Falbum95751036_0%2Frev
Преподаватель: Коломиец Светлана Григорьевна