Утверждение 3.1: Наименьшего элемента в L нет.
Доказательство:
Допустим противное, то есть пусть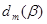 
- наименьший в L элемент. Тогда 
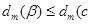Ø), где сØ – нигде неопределенная функция.
Следовательно, 
Ø и 
(сØ).
Возьмем всюду определенную функцию h. Ясно, что сØ≤mh.
С одной стороны, 
(сØ) – наименьший элемент, то есть сØ≤mh; с другой стороны сØ≤mh.
Получили противоречие, то есть в L наименьшего элемента нет. Ч.т.д.
Утверждение 3.2: m-степень, содержащая универсальную функцию, является наибольшей в L.
Доказательство:
Пусть Ψ – универсальная функция, а α – произвольная ЧРФ. Так как α – ЧРФ, то найдется такое число х0, что α=φ0.
Покажем, что 
. В качестве сводящей возмем функцию f(x0,y). Тогда из определения Ψ вытекает, что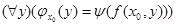 
, где 
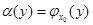, то есть 
.
Таким образом, 
- наибольшая в L. Ч.т.д.
Введем обозначение: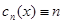 
.
Ясно, что 
.
Утверждение 3.3: сØ и множество всех функций вида cn(x) и только они образуют множество минимальных в L элементов.
Доказательство.
Из утверждения 3.1. следует, что сØ – минимальный в L элемент.
Возьмем произвольную функцию cn(x).
Пусть 
.
Ясно, что 
{ 
}, кроме того α – всюду определенная функция, так как иначе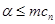 
, следовательно, 
.
Пусть теперь 
минимальный в L элемент, отличный от сØ и от всех сn, тогда 
определена в некоторой точке х0; пусть 
, имеем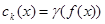 
, где 
, то есть, 
. Получили противоречие. Ч.т.д. [1,2]
Практическая часть.
Идеалы полурешетки m-степеней частично рекурсивных функций
Определение:
Идеалом полурешетки L назовем всякое подмножество I отличное от Ø, удовлетворяющее следующим условиям:
1. 
;
2. 
.
Идеал называется главным, если он содержит наибольший элемент.
Рассмотрим множество всех m-степеней частичных характеристических функций, то есть:
Н={ 
}.
Предположение 4.1:
Множество Н является главным идеалом полурешетки L.
Доказательство:
1. Берем две степени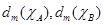 
для некоторых р.п. множеств А и В. точной верхней гранью будет степень, содержащая функцию 
.
Определим множество А 
В:
{ 
}.
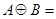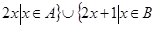Докажем, что 
.
Будем пользоваться определением 15 для доказательства данного равенства.
Рассмотрим 4 случая.
1) если x=2t, 
И если x=2t, 
2) Если x=2t, 
И если x=2t, 
3) Если x=2t+1,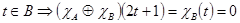 
И если x=2t+1,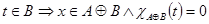 
4) Если x=2t+1, 
И если x=2t+1, 
Следовательно, равенство 
справедливо во всех четырех случаях, т.к. обе его части равносильны в рассмотренных случаях.
.
2. Пусть 
. По определению m-сводимости из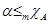 
следует, что существует рекурсивная функция f такая, что: 
, откуда 
. Из утверждения 2.2 и того, что всякое р.п. множество m-сводимо к креативному следует, что: 
- наибольший элемент в Н, где k – креативно.
Тогда Н – главный идеал полурешетки L. Ч.т.д.
Рассмотрим множество всех m-степеней рекурсивных функций, то есть:
М={ 
}.
Предположение 4.2: Данное множество М является главным идеалом полурешетки L.
Доказательство:
1. Берем две степени рекурсивных функций, их точной верхней гранью будет 
, где 
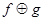также рекурсивная функция.
2. Если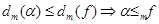 
, откуда существует рекурсивная функция h, такая, что 
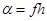, где 
также рекурсивная функция. Далее, 
посредством f(x) для любой рекурсивной функции f(x), отсюда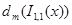 
- наибольший элемент в М.
М – главный идеал полурешетки L. Ч.т.д.
Литература
1. Дегтев А.Н. Сводимость частично-рекурсивных функций. – Сибирский математический журнал, 1975 т. 16, №5, с. 970-988.
2. Ершов Ю.Л. Теория нумераций. – М.: Наука, 1977.
3. Кагленд Н. Вычислимость. Введение в теорию рекурсивных функций. – М.: Мир, 1983.
4. Мальцев А.И. Алгоритмы и рекурсивные функции. – М.: Наука, 1965.
5. Поляков Е.А., Розинас М.Г. Теория алгоритмов. – Иваново: ИвГУ, 1976.
6. Поляков Е.А., Маринина Н.В. Теория алгоритмов. – Шуя: ШГПУ, 2004.
7. Роджерс Х. Теория рекурсивных функций и эффективная вычислимость. – М.: Мир, 1972.