Занятие №3. «Пространственная система сил. Трение»

Задание № 1.

Тема: «Пространственная система сил. Трение»

Выполнил студент группы 222-ЧС ____________________________

 

ЗАДАНИЕ ДИСТАНЦИОННОГО ОБУЧЕНИЯ

 

Изучить тему занятия №1 «Пространственная система сил. Трение». В рабочей тетраде письменно ответить на вопросы. После вопроса напечатать слово ОТВЕТ и напечатать (написать) ответ:

Вопросы и здания

 

1. Что такое пространственная система сил сходящаяся пространственная система сил?

2. Каким образом раскладывается (проецируется) сила на три оси координат (с иллюстрацией) и какой вывод из этого следует?

3. Чему равен модуль силы, расположенной в пространственной системе координат?

4. По рисунку 2 пользуясь формулами направляющих косинусов, определите проекции силы F = 10 Н на оси x, y и z, если все углы между осями и вектором силы F равны 45° (cos 45° = 0,707).

5. Что такое момент силы относительно оси?

6. По рисунку 3 определите момент силы F = 10 Н относительно оси червяного колеса, если угол между вектором силы F и ее проекцией F ₁ равен 30° (cos 30° = 0,606).

7. Каково правило знаков моментов сил относительно осей?

8. В чем заключаются законы трения?

9. Какие бывают и как определяются силы трения?

10. Что такое конус трения, от чего он зависит и как определяется угол конуса трения?

11. Как определяется момент трения качения и от чего зависит его величина?

Занятие №3. «Пространственная система сил. Трение»

 

Система сил, линии действия которых расположены в раз­личных плоскостях, называется пространственной системой сил.

Пространственная система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.

Теорема. Пространственная система сходящихся сил экви­валентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил: F_Σ = ΣF_i

Проекция силы на ось в пространстве. Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графи­ческий способы нахождения равнодействующей неприемлемы, а применяется аналитический способ (метод проекций).

Если сила и ось не лежат в одной плоскости, то проецирующие перпендикуляры также не лежат в одной плоскости (рис. 1).

 

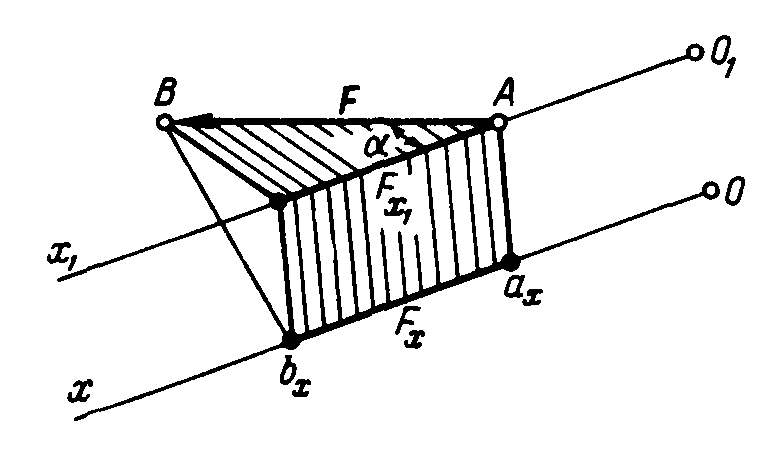
Рис. 1. Проекция силы на ось в пространстве

 

Для того чтобы определить, чему равна проекция силы Р на ось Ох, следует мысленно провести через начало или конец силы ось Ox, параллельную данной оси Ох, тогда Р_х = Рсosα, так как Р_x = Р_x1.

Правило знаков для проекций остается прежним.

Если вектор силы параллелен оси, то он проецируется на эту ось в натуральную величину.

Если вектор силы лежит в плоскости, перпендикулярной оси, то его проекция на эту ось равна нулю.

Разложение силы по трем осям координат. Пусть дана сила F (рис. 2). Возьмем систему координат так, чтобы начало координат совпадало с началом вектора силы F. Из конца этого вектора опустим перпендикуляр на плоскость ху и разложим силу F на составляющие F_ху и F_z, а составляющую F_х — на составляющие F_х и F_y. Тогда F = F_х + F_y + F_z

Достроим полученное изображение до параллелепипеда, у которого составляющие F_х, F_y, F_z являются ребрами, а сила F — диагональю.

Из изложенного можно сделать такой вывод: равнодейст­вующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах.

Из рис. 2видно, что в случаях разложения силы F по трем взаимно перпендикулярным направлениям х, у, z состав­ляющие F_х, F_y, F_z равны по модулю проекциям силы F на эти оси. Эти проекции обозначим F_х, F_y, F_z.

 

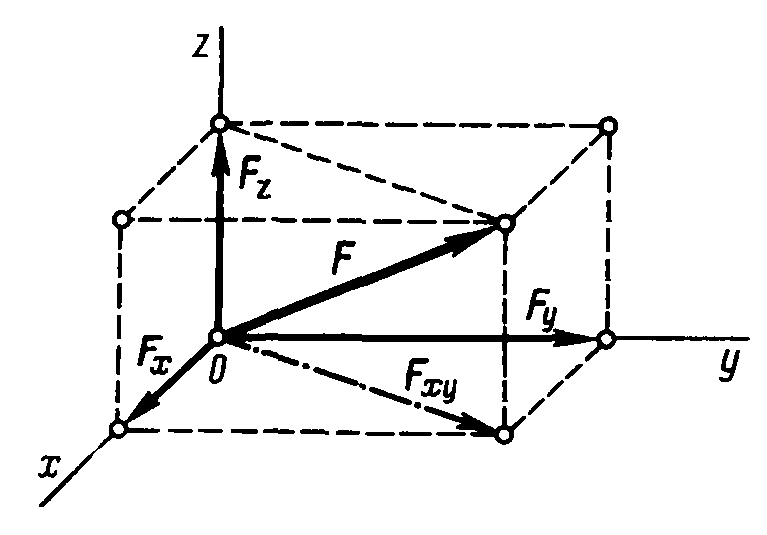
Рис. 2. Проекции силы F на оси координат.

 

Зная проекции силы на три взаимно перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:

модуль силы

 

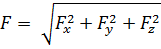
направляющие косинусы:

 

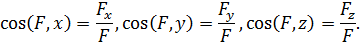
Момент силы относительно оси. Рассмотрим колесо червячной передачи, укрепленное на валу, вращающемся в подшипниках (рис. 3).

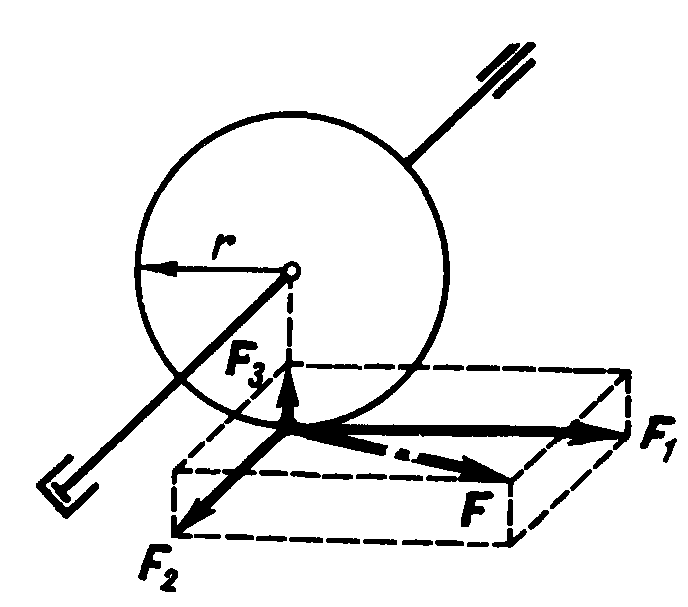
Рис. 3. Силы, действующие на червячное колесо.

 

Червяк передает червячному колесу усилие F, не лежащее в плоскости, перпенди­кулярной оси.

Разложим силу F на три вза­имно перпендикулярные составля­ющие F₁, F₂ и F₃. Составляющую F₁ назовем окружным усилием, составляющую F₂ — осевым усили­ем, а составляющую F₃ — радиаль­ным усилием.

Составляющая F₁ вызывает вра­щательное действие, которое изме­ряется произведением F ₁ r; состав­ляющая F ₂ стремится сдвинуть ко­лесо вдоль оси, составляющая F₃ стремится изогнуть ось колеса, а вращательное действие этих сил относительно оси равно нулю.

Таким образом, если нужно найти момент силы относи­тельно оси, то следует принимать в расчет только состав­ляющую F₁, лежащую в плоскости, перпендикулярной оси, и не пересекающую ось.

Ранее было установлено, что проекция вектора силы на ось есть скалярная алгебраическая величина. В отличие от проекции на ось проекция силы на плоскость есть величина векторная, так как эта проекция характеризуется не только числовым значением, но и положением на плоскости, т. е. направлением. Поэтому моменту силы относительно оси можно дать такое определение: моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересече­ния оси с плоскостью.

Это определение пояснит рис. 4.

Момент силы относи­тельно оси условимся записы­вать следующим образом:

 

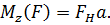
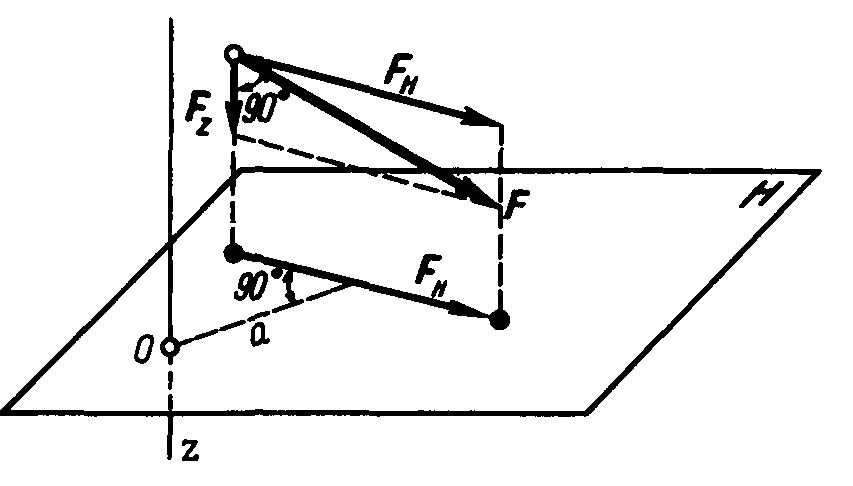
Рис. 4. Определение момента силы относительно оси.

Условимся считать момент силы положительным, если смотреть с положительного конца оси и сила стремится вызвать вращение против часовой стрелки, и наоборот.

Момент силы относительно оси не меняется от перемеще­ния силы вдоль линии ее действия.

Момент силы относительно оси равен нулю в двух случаях (не считая случаев, когда сила равна нулю или действует вдоль оси):

1) если вектор силы параллелен оси, так как при этом проекция силы на плоскость, перпендикулярную оси, равна нулю (см. силу F₂ на рис. 3);

2) если линия действия силы пересекает ось, так как при этом плечо равно нулю (см. силу F₃ на рис. 3).

 

Трение

 

Давно известно, что, если двигать одно тело по поверхности другого, в плоскости соприкосновения возникает сила сопротив­ления относительному скольжению этих тел. Впервые исследова­ниями явления трения занимался Леонардо да Винчи. Точное определение силы трения с учетом всех факторов, от которых она зависит, представляет столь сложную задачу, что до сих пор не удается найти полного теоретического решения. Поэтому при изучении законов трения приходится основываться на результатах экспериментов.

Итак, законы трения были найдены опыт­ным путем и в 1771 г. сформулированы фран­цузским ученым Кулоном.

 

Законы трения

1. Сила трения направлена в сторону, про­тивоположную относительной скорости сколь­жения (рис. 5).

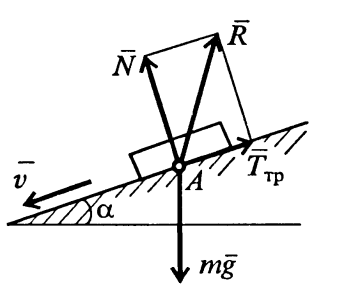
Рис. 5. Иллюстрация к 1-му закону трения

 

2. Сила трения не зависит от площади трущихся поверхностей.

3. Модуль силы трения пропорционален нормальному давлению.

 

Различают силу трения при покое и при движении:

 

Сила трения покоя	Сила трения при движении

 

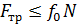
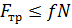
где N – сила нормального давления, f ₀ – коэффициент трения покоя, f – коэффициент трения скольжения.

Максимальная вели­чина силы трения F _{тр max} = f _o N. Из экспериментов известно, что при движении коэффициент трения скольжения зависит от скоро­сти скольжения тел.

Коэффициенты f ₀ и f зависят от материала и физического со­стояния трущихся поверхностей. Значения этих коэффициентов приведены в табл. 1.

 

Таблица 1

Коэффициенты трения скольжения

 

Материал	Коэффициент трения
покоя f 0	скольжения f
Камень по камню	0,6...07	–
Бетон по галечнику	0,5...0,6	–
Веревка по дереву	0,5...0,8	0,5
Дерево по дереву	0,4...0,7	0,3
Металл по дереву	0,4...0,6	0,3...0,5
Бетон по песку	0,3...0,4	–
Камень по дереву	0,4	–
Кожа по металлу	0,3...0,4	0,3
Асбестовая обкладка по стали (чугуну)	0,25...0,35	–
Бронза по чугуну	0,16	–
Бронза по чугуну с обильной смазкой	0,12	–
Сталь по льду	0,03	0,015
Сталь по чугуну, сталь по стали, чугун по чугуну	0,12...0,2	0,1

 

На шероховатой поверхности сила трения может колебаться от нуля до максимального значения, т. е. 0 < F _тp < F _{тр max}. В этом случае реакция связи R будет N<R< R_max. Наибольший угол φ, на который полная реакция R может отклоняться, называется углом трения:

 

 

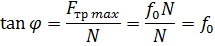
В зависимости от направления приложенной к телу силы мак­симальная реакция связи R _max может иметь различные направления, образуя при этом геометрическое место в пространстве в виде конической поверхности с вершиной в точке касания тела, назы­ваемой конусом трения. Если приложенная к телу сила проходит внутри конуса трения, то тело находится в равновесии.

Трением качения, или трением второго рода, называют сопро­тивление, возникающее при качении одного тела по-другому. Рассмотрим цилиндрический каток радиусом r и весом mg, ле­жащий на шероховатой поверхности. Приложим в центре катка силу Q (рис. 6, а), которая будет меньше, чем F _{тр max}: Q < F _{тр max}.

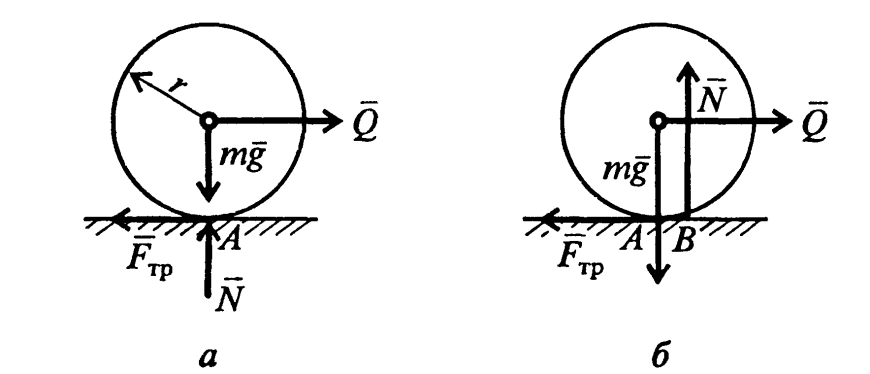
Рис. 6. Трение каечения.

 

Возникнет сила трения F _тр, препятствующая скольжению точки А по плоскости. В этом случае mg и N уравновешиваются, a F _три Q образуют пару сил и каток должен катиться по плоскости.

В действительности, если Q < Q _пред, каток остается в состоянии покоя. Для объяснения этого явления необходимо в рассуждения внести следующие коррективы (рис. 6, б):

 

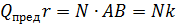
Входящий в это выражение коэффициент k называется коэффи­циентом трения качения; он измеряется в см. Следовательно, воз­никает момент трения качения

 

М _тр = kN.

 

Значения коэффициента трения качения приведены в табл. 2.

 

Таблица 2