Элементы математической статистики.
Основные понятия и термины: комбинаторика, элементы комбинаторики, перестановка, факториал, сочетания, размещения
Комбинато́рика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Перестановкой из n элементов (например чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов.
Пусть имеется n различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно Pn=n!=1⋅2⋅3⋅...⋅(n−1)⋅n
Символ n! называется факториалом и обозначает произведение всех целых чисел от 1 до n. По определению, считают, что 0!=1,1!=1


Множество n=3 элементов Перестановки (всего P3=3!=1⋅2⋅3=6)
Число всех перестановок порядка n равно факториалу: Pn=n!
Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно.
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел. Например,
1! = 1,
2! = 2•1 = 2,
3! = 3 •2 •1 = 6,
4! = 4 •3 •2 •1 = 24,
С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов – уже 3 628 800 (больше 3 миллионов!).
Задача. Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?
Решение:
На первое место можно положить любой из четырех шариков, на второе – любой из трех оставшихся, на третье – любой из двух оставшихся, а на четвертое – последний оставшийся шарик. Итак, ответ: 4 • 3 • 2 • 1 = 4!.
Задача. На танцплощадке собрались 7 юношей и 7 девушек. Сколькими способами они могут разбиться на пары для участия в очередном танце? (выбрать 7 пар)
Ответ: 7!=7·6·5·4·3·2·1=5040
Правило умножения заключается в том, что для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Задача. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9?
Решение. Перечислим все возможные варианты:
20 22 26
30 32 36
60 62 66
70 72 76
90 92 96
Используя правило умножения, получаем: 5х3=15 (с нуля число не может начинаться, поэтому 5, четные цифры 0,2,6)
Задача. Имеется три класса учеников. В первом классе 15 человек, во втором 17, в третьем -20. Нужно выбрать 3 ученика из каждого класса. Сколькими способами можно это сделать?
Решение: Из первого класса выбираем ученика 15 способами, из второго 17 способами, из третьего -20 способами. Всего способов 15·17·20=5100
Задача. Имеются пять видов конвертов без марок и четыре вида марок. Сколькими способами можно выбрать конверт с маркой для посылки письма?
Ответ: 20
Сочетания из n элементов по m


Множество n=3 элементов Сочетания по 2 элемента
Пусть имеется n различных объектов. Будем выбирать из них m объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по m, а их число равно

Пример всех сочетаний из n=3 объектов (различных фигур) по m=2- на картинке. Согласно формуле, их должно быть ровно
C23=3!/2!(3−2)! =3. Ясно, что сочетаний всегда меньше чем размещений (так как при размещениях порядок важен, а для сочетаний - нет), причем именно в m! раз.
Задача. Сколько экзаменационных комиссий, состоящих из 3 членов, можно образовать из 10 преподавателей?
Решение: По формуле находим:
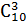 =
=  120 комиссий
120 комиссий
Ответ: 120 комиссий.