Давление насыщенных паров

Анализируя материал предыдущего раздела можно сформулировать другое определение давления насыщенных паров – это давление пара, находящегося в равновесии с жидкостью при данных термодинамических условиях и соотношении объемов фаз. Такая характеристика позволяет судить о склонности нефтей и нефтепродуктов к образованию паровых пробок, например в трубопроводе, потерях при испарении и хранении в резервуарах и т.д., и является основным показателем испаряемости и стабильности товарных нефтепродуктов.

(1.19)

Давление насыщенных паров р _S химически однородных жидкостей и азеотропных (не изменяющих свой состав в процессе испарения) веществ изучено достаточно хорошо. Установлено, что р _S зависит от температуры и может быть определено с помощью простой формулы:

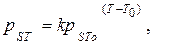где р_ST – давление насыщенных паров при температуре Т; р_STo – давление насыщенных паров при известной температуре Т_о; k – эмпирический коэффициент.

Давление р _S паров индивидуальных углеводородов и нефтяных фракций можно определить, пользуясь различными графиками или например табл. 1.8.

(1.20)

Для смеси жидких углеводородов согласно закону Рауля давление насыщенных паров зависит от давления насыщенных паров отдельных компонентов и от мольных концентраций. Парциальное давление р_i любого компонента в жидкой смеси равно произведению давления насыщенного пара р_Si чистого компонента на его мольную концентрацию х_i в чистом виде, т.е. упругость паров жидкости равна сумме давлений компонентов этой смеси, которую они бы имели, если бы каждый занимал при данной температуре весь объем смеси, т.е. сумме парциальных давлений, или согласно закону Дальтона (1802 г.) парциальное давление р_i компонента, входящего в состав паровой фазы, равно произведению мольной концентрации компонента в паровой фазе на общее давление, т.е

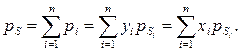(1.21)

р_i = р_Sy_i. (1.22)

Таким образом, из уравнений (1.21÷1.22) имеем

х_iр_Si = р_Sy_i. (1.23)

Уравнение (1.23) известно под названием объединенного закона Дальтона – Рауля, согласно которому можно сделать важный вывод – в состоянии равновесия парциальное давление любого компонента смеси в паровой фазе равно парциальному давлению того же компонента в жидкости.

Из приведенного уравнения следует, что

р_Si/p_S = y_i/x_i = k_i = const

или

р_Si = k_piр_S и y_i = k_pix_i. (1.24)

Коэффициент k_рi, который называют константой равновесия, у отдельных компонентов зависит от температуры и давления и определяется, как правило, из специально составленных графиков. Приведенные уравнения позволяют, например, найти состав газовой фазы по известному составу жидкостей и наоборот.

Константы равновесия (в зарубежной литературе больше известны как константы фазового распределения) дают возможность прогнозировать материальный баланс многокомпонентных двухфазных систем (концентрации компонентов в разных фазах) при условии, если заданы давление и температура и известна также молярная концентрация i -го компонента в однофазном состоянии x_i⁰.

При определении давления насыщенных паров нефтей и нефтепродуктов на практике необходимо учитывать два случая:

· когда объем паровой фазы V_П по сравнению с объемом жидкой фазы V_Ж невелик, можно считать, что в состоянии насыщения состав жидкой фазы не меняется и что последняя находится в равновесии с насыщенным паром;

· когда V_П значительно больше V_Ж, испарение наиболее летучих компонентов продукта приводит к изменению состава жидкости и в состоянии насыщения пар находится в равновесии с жидкостью, но уже измененного состава. Давление пара в этом случае будет отличаться от давления пара, определенного для небольшого объема V_П и будет тем больше, чем меньше соотношение V_П/V_Ж.

Давление р _S при объеме паровой фазы, близком к нулю, принимает максимальное значение и определяется давлением паров наиболее легких углеводородов:

· Рейда, заключающимся в регистрации по манометру избыточного давления насыщенных паров нефтепродуктов, помещенном в специальную «бомбу» и нагретым до 37,8ºС (»38ºС), причем соотношение жидкой и паровой фаз в бомбе Рейда составляет 1:4 (ГОСТ 1756-52);

·

методом Валявского-Бударова, основанным на определении изменения объема паров смеси при нагреве нефтепродуктов до 37,8ºС в стеклянном приборе, при этом соотношение жидкой и паровой фаз принято равным 1:1.

 

Вязкость

Одной из наиболее характерных особенностей жидкостей является способность изменять свою форму, под действием внешних сил. Это свойство жидкости объясняется скольжением ее молекул относительно друг друга. Одна и та же сила создает в разных жидкостях разные скорости перемещения слоев, отстоящих один от другого на одинаковые расстояния. Однако способность молекул к скольжению не бесконечно велика, поэтому Ньютон рассматривает вязкость как «недостаток скольжения». Обычно вязкостью или внутренним трением называют свойство жидкости сопротивляться взаимному перемещению ее частиц, вызываемому действием приложенной к жидкости силы.

явление внутреннего трения в жидкости с ее вязкостью было связано Ньютоном известной формулой

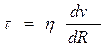(1.39)

где t – напряжение внутреннего трения; dv/dR – градиент скорости по радиусу трубы или относительное изменение скорости по направлению, перпендикулярному к направлению течения, т.е. приращением скорости на единицу длины нормали; η – коэффициент (касательное усилие на единицу площади, приложенное к слоям жидкости, отстоящим друг от друга на расстоянии, равном единице длины, при единичной разности скоростей между ними).

Внутреннее трение, характеризуемое величиной η, немецкий ученый М. Якоб в 1928 году предложил называть динамической вязкостью. В технической литературе за η утвердилось наименование абсолютной вязкости, т.к. эта величина выражается в абсолютных единицах. Однако в абсолютных единицах можно выражать также и единицы кинематической и удельной вязкости. Термин «динамическая вязкость» соответствует физическому смыслу η, т.к. согласно учению о вязкости η входит в уравнение, связывающее силу внутреннего трения с изменением скорости на единицу расстояния, перпендикулярного к плоскости движущейся жидкости.

Впервые же динамическая вязкость была выведена врачом Пуазейлем в 1842 г. при изучении процессов циркуляции крови в кровеносных сосудах. Пуазейль применил для своих опытов очень узкие капилляры (диаметром 0,03÷0,14 мм), т.е. он имел дело с потоком жидкости, движение которого было прямолинейно послойным (ламинарным). Вместе с тем исследователи, работавшие до Пуазейля, изучали закономерность истечения жидкости в более широких капиллярах, т.е. имели дело с возникающим турбулентным (вихревым) истечением жидкости. Проведя серию опытов с капиллярами, соединенными с шарообразным резервуаром, через которые под действием сжатого воздуха пропускался некоторый объем жидкости, определенный отметками, сделанными сверху и снизу резервуара, Пуазейль пришел к следующим выводам: 1) количество жидкости, вытекающее в единицу времени, пропорционально давлению при условии, что длина трубки превышает некоторый минимум, возрастающий с увеличением радиуса; 2) количество жидкости, вытекающее в единицу времени, обратно пропорционально длине трубки и прямо пропорционально четвертой степени радиуса. Формула Пуазейля в современной редакции выглядит следующим образом:

где η – коэффициент внутреннего трения (динамическая вязкость); Р – давление, при котором происходило истечение жидкости; τ – время истечения жидкости в объеме V, L – длина капилляра; r – радиус капилляра.

Единицей динамической вязкости является сила, необходимая для поддержания разности скоростей, равной 1 м/с, между двумя параллельными слоями жидкости площадью 1 м² находящимися друг от друга на расстоянии 1 м, т.е. единицей измерения динамической вязкости в системе СИ является

Н × с/м² или Па × с.

Единица динамической вязкости, выраженная в физической системе измерения СГС, в честь Пуазейля называется пуазом, т.е. за единицу динамической вязкости принимают сопротивление, которое оказывает жидкость при относительном перемещении двух ее слоев площадью 1 см², отстоящих друг от друга на 1 см, под влиянием внешней силы в 1 дн при скорости перемещения в 1 см 1 с. Динамическую вязкость при температуре t обозначают η_t.

Приближенное совпадение численного значения динамической вязкости воды при 20°С с 1 сантипуазом (сП) дало повод Бингаму предложить построить систему единиц вязкости, в которой исходной единицей является динамическая вязкость воды при 20°С, принимаемая по Бингаму за 1 сП (точнее η₂₀ воды равна 1,0087 сП). Таким образом, для большинства практических измерений с достаточной точностью можно считать, что η ₂₀ воды соответствует 1 сП. Это представляет большое удобство в практической вискозиметрии, для которой большое значение имеют жидкости с постоянными физико-химическими константами, имеющие точно известную вязкость при данной температуре. Из числа относительных обозначений наибольшим распространением пользуется так называемая удельная вязкость, показывающая, во сколько раз динамическая вязкость данной жидкости больше или меньше динамической вязкости воды при какой-то условно выбранной температуре. Таким образом, удельная вязкость представляет собой отвлеченное число.

Величина, обратная динамической вязкости, носит название текучести и обозначается знаком Т.

Вязкость нефтей и нефтепродуктов зависит от температуры, увеличиваясь с ее понижением. Наибольшее применение для практических расчетов подучила формула Рейнольдса-Филонова

		(1.42)
		(1.43)

 

 

где u – коэффициент крутизны вискограммы, 1/К; n^*, n – кинематическая вязкость при известной температуре Т_ж и при температуре Т; e – основание натурального логарифма.

(1.41)

Для нахождения коэффициента крутизны вискограммы для данного продукта достаточно знать значения вязкостей при двух температурах Т₁ и Т₂..

Динамическая и кинематическая вязкости – это вполне определенные физические характеристики, которые, как и все другие величины, выражены в абсолютных единицах и могут быть подставлены в те или другие расчетные формулы. В случаях, когда вязкость применяется не как расчетная величина, а как практическая характеристика нефтепродукта, ее принято выражать не в абсолютных, а в относительных, или условных, единицах.

Подобный способ выражения вязкости является результатом неправильного представления о том, что определение динамической и кинематической вязкостей отличается сложностью, и применения на практике упрощенных технических приборов, дающих показания в условных единицах вязкости. Неудобство всех условных, или относительных, единиц вязкости заключается в том, что вязкость, выраженная в этих единицах, не представляет собой физической характеристики нефтепродукта, т.к. она зависит от способа определения, конструкции прибора и других условий. Из числа относительных обозначений наибольшим распространением пользуется так называемая удельная вязкость.

В различных странах в зависимости от выбора стандартных аппаратов для определения условной вязкости приняты различные условные единицы вязкости. Для пересчета в абсолютные единицы существуют эмпирические формулы, однако все эти формулы носят лишь приближенный характер, а некоторые из них просто неточны. Поэтому, если необходимо определить вязкость нефтепродукта в абсолютных единицах, следует определять ее непосредственно и только в крайних случаях прибегать к пересчету. Условную вязкость выражают условными единицами: градусами или секундами. Эти единицы обычно представляют собой либо отношение времени истечения определенного объема исследуемого продукта при данной температуре ко времени истечения такого же объема стандартной жидкости при определенно установленной температуре, либо просто время истечения определенного объема испытуемой жидкости.

Как сказано выше, вязкость характеризует свойство данной жидкости оказывать сопротивление при перемещении одной части жидкости относительно другой. Такое сопротивление наблюдается как при движении жидкости относительно какого-либо тела, так и при движении какого-либо тела в жидкости. Оба эти случая дают принципиальную возможность измерения вязкости различными способами. Наиболее удобным способом измерения вязкости при движении жидкости относительно твердого тела является наблюдение над истечением исследуемых жидкостей из капиллярных трубок. Для расчета пользуются формулой Пуазейля. Для расчета значений вязкости при движении каких-либо тел в жидкости может быть применен ряд формул, в которых учитываются характер движе­ния и форма движущегося тела. Из этих формул наибольшее значение имеет приводимая ниже формула Стокса для расчета вязкости по скорости падения твердого шарика в жидкости. Способы измерения вязкости, основанные на истечении жидкости из капиллярных трубок, широко распространены. Напротив, способы, построенные на принципе движения твердого тела определенной формы в вязкой жидкости, применяются сравнительно редко вследствие того, что даже для тел простейшей формы соответствующие уравнения движения получаются очень сложными. Эти способы находят себе применение преимущественно в тех случаях, когда способы, основанные на втором принципе, т.е. на истечении жидкости из капилляров, практически неприменимы вследствие экспериментальных трудностей.