Им. Р.Е. Алексеева»
АРЗАМАССКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
Расчетно – графическая работа
По дисциплине
«Моделирование систем»
| Выполнил студент группы | АЗИС 2013-1 | Рябов С.В. | ||
| Проверил | ст. преп., к.ф.-м.н. | Мазуров А.Ю. | ||
Арзамас
2016 г.
Задание 1
Минимизация функции методом парабол
В результате проведения эксперимента получены числовые данные для входных параметров X и выходных параметров Y. Данные представлены в Таблице 1.
Таблица 1:
| X | 0,5 | 1,5 | 2,5 |
| Y | 0,125 | 0,375 | 5,625 |
Аппроксимировать зависимость y = f(x) с помощью:
а) метода наименьших квадратов, используя прямую y = kx + b;
б) метода парабол.
В каждом случае, найти минимальное значение выходного параметра по построенной аппроксимирующей функции на отрезке [0.4, 4].
Краткое описание минимизации функции методом парабол:
Минимизируемая функция аппроксимируется в достаточно малой окрестности полиномом n-й степени. Для использования полинома достаточно высокой степени требуется сужение отрезка аппроксимации. Сходимость данного метода может быть гарантирована лишь для достаточно регулярных функций (непрерывных и много раз дифференцируемых).
В этом методе вычисляется значение функции сразу в трех близлежащих точках 
, 
, 
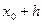, где h – малое число. Через эти три точки проводится интерполяционная парабола: 
. Минимум параболы достигается при 
, т.е. при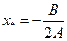 
. Для трех точек получаем систему линейных уравнений для коэффициентов A, B, C.
Аппроксимация функции методом парабол
Текст программы:
clear all; clc; clf;
%исходные данные
x = [0.5 1.5 2.5]; %координаты X
|
|
y = [0.125 0.375 5.625]; %координаты Y
a = 0.4; %начальная точка отрезка
b = 4; %конечная точка отрезка
stp = 0.1; %шаг построения графика
%расчеты
M = [x(1)^2 x(1) 1; x(2)^2 x(2) 1; x(3)^2 x(3) 1];
F = [y(1);y(2);y(3)];
cf = inv(M)*F;
px = a:stp:b; py = cf(1).*px.^2+cf(2).*px+cf(3);
xmin = -cf(2)/(2*cf(1))
ymin = cf(1)*xmin^2+cf(2)*xmin+cf(3)
%построение графиков
plot(px,py);
hold on;
plot(x,y,' bo','MarkerFaceColor','w','MarkerSize',6);
hold on;
plot(xmin,ymin,' ro','MarkerFaceColor','r','MarkerSize',6);
Результат работы программы:
xmin = 0.9500 ymin = -0.3813
Снимок рабочего окна:
Снимок окна с графиком функции:
Аппроксимация функции методом наименьших квадратов
Текст программы:
clear all; clc; clf;
%исходные данные
x = [0.5 1.5 2.5]; %координаты X
y = [0.125 0.375 5.625]; %координаты Y
a = 0.4; %начальная точка отрезка
b = 4; %конечная точка отрезка
stp = 0.1; %шаг построения графика
%расчеты
a1 = 0; a2 = 0;
b1 = 0; b2 = 0;
sx = size(x,2);
for i = 1:1:sx
a1 = a1+x(i); a2 = a2+x(i)^2;
b1 = b1+y(i); b2 = b2+x(i)*y(i);
end
M = [sx a1; a1 a2];
D = [b1; b2];
cf = inv(M)*D;
px = a:stp:b; py = cf(2).*px+cf(1);
xmin = min(px)
ymin = min(py)
%построение графиков
plot(px,py);
hold on;
plot(x,y,' bo','MarkerFaceColor','w','MarkerSize',6);
hold on;
plot(xmin,ymin,' ro','MarkerFaceColor','r','MarkerSize',6);
Результат работы программы:
xmin = 0.4000 ymin = -0.9833
Снимок рабочего окна:
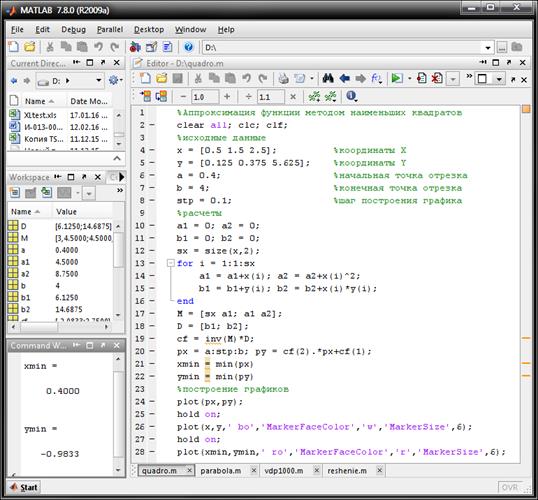
Снимок окна с графиком функции:
Задание 2
Постановка задачи:
Используя метод Рунге-Кутта (решатель ode45), найти численное решение системы обыкновенных дифференциальных уравнений с заданными начальными условиями:
на временном интервале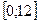 
Построить графики решений 
Краткое описание метода решения:
Большой класс обыкновенных дифференциальных уравнений, а именно, уравнения с одной независимой переменной, разрешенные относительно старшей производной, могут быть сведены к системе дифференциальных уравнений 1-го порядка вида
|
|
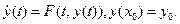
Если правые части соответствующей системы достаточно гладкие функции, то описываемая система имеет единственное решение, которое может быть получено численно с помощью одного из алгоритмов MATLAB.
Текст программы:
Программа для вызова решателя обыкновенных дифференциальных уравнений ode45 (отдельный М - файл)
% вызов решателя Рунге-Кутта
[T,Y] = ode45(@vdp1000,[0 12],[0 1 1]);
% вывод результата на экран
plot(T,Y(:,1),'-o','MarkerFaceColor','w','MarkerSize',5);
Функция vdp1000
(отдельный М - файл)
function dy = vdp1000(t,y)
% вектор-столбец
dy = zeros(3,1);
% уравнения системы
dy(1) = y(2)*y(3);
dy(2) = -y(1)*y(3);
dy(3) = -0.51*y(1)*y(2);
Снимок рабочего окна:
Снимок окна с графиком функции:
Задание 3
Постановка задачи:
Используя Matlab / Simulink, построить соответствующую схему и найти численное решение обыкновенного дифференциального уравнения с заданными начальными условиями:
; y(1) =0.5, y’(1)=3; 1 ≤ x ≤ 2.
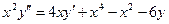
Сравнить численное решение с аналитическим решением: 
Снимок схемы рабочего окна:
Снимок окна с графиками функции (числовое и аналитическое решения):
Снимок окна с графиком функции (разница числового и аналитического решения):
