Основные теоретические сведения
Удар – кратковременное взаимодействие тел.
Центральным называют удар, при котором скорости взаимодействующих тел направлены вдоль прямой, соединяющей их центры масс.
Абсолютно упругим называют удар, при котором действуют лишь консервативные силы и поэтому механическая энергия системы взаимодействующих тел сохраняется.
Абсолютно неупругим называют удар, при котором после взаимодействия тела движутся как единое целое (с одинаковой скоростью).
Механическая система – совокупность тел (материальных точек), рассматриваемых как единое целое. Механическая система тел, на которую не действуют внешние тела, называется замкнутой.
Импульс системы тел равен векторной сумме импульсов 
всех n тел, входящих в систему:
.
Закон сохранения импульса (ЗСИ): в замкнутой механической системе
,
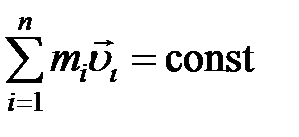ЗСИ для упругого центрального удара двух тел
,
ЗСИ для неупругого центрального удара двух тел
,
где 
, 
– скорости тел непосредственно перед ударом;
, 
, 
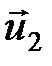– скорости тел после удара.
Коэффициент восстановления механической энергииk – отношение кинетических энергий системы тел: после удара Е к энергии до удара Е 0:
.
Он характеризует рассеяние механической энергии при ударе и зависит от упругих свойств взаимодействующих тел. Для абсолютно упругого удара k = 1, в реальных случаях (неабсолютно упругий удар) k < 1.
Описание установки
Установка состоитиз горизонтально расположенного рабочего поля3 (рис.1)с нанесенной координатной сеткой, по которому перемещаются взаимодействующие тела 1 и 2. Начальную скорость телу 1 в направлении оси Ox сообщает ударный пружинный механизм 5. Перед выстрелом тело 1 фиксируется между направляющими 6. Ударный механизм снабжен винтом 4, изменяя положение которого, можно изменять начальный импульс тела 1.
|
|
| Рис. 1 |
| Y |
| X |
Вывод расчетных формул
Боёк ударного пружинного механизма, ударяя по телу 1 (рис.2), сообщает ему начальный импульс, значение которого перед взаимодействием тел
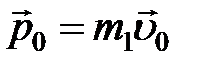, (1)
где m 1– масса первого тела,
–начальная скорость тела.
Начальную скорость тела u 0 можно оценить по длине пути l 0, пройденному телом по рабочему полю до остановки при свободном движении. Работа силытрения по определению равна 
. По теореме о кинетической энергии эта работа равна приращению энергии тела
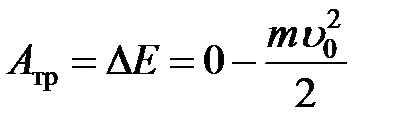. (2)
Учитывая это, найдем начальную скоростьтела
. (3)
Следует отметить, что u 0–скорость шайбы в момент соударения, когда она находится на расстоянии l 0 от точки, где оно остановится.
После взаимодействия тела начинают двигаться со скоростями 
и 
соответственно.
Их суммарный импульс:
, (4)
гдескорость первого и второго тел после взаимодействия равны соответственно
, (5)
l 1, l 2– расстояния, проходимые телами после взаимодействия.
Длину пути l 0 при свободном движении тела 1 (в отсутствие второго тела), а также после соударения l 1 и l 2, определяют по изменению координат x и y крайних точек тел (рис. 2) при помощи теоремы Пифагора.
|
|
(6)
| х 01 221 |
| у 1 |
| х 1 |
| х 2 |
| у 2 |
| х |
| l 1 |
| l 2 |
| l 0 |
| у 02 2 |
| х х 02 01 |
| у 01 11 |
| Y |
| X |
Рис. 2
В случае нецентрального удара, первое тело продолжит движение под угломa к направлению оси Ox. При этом:
. (7)
Второе тело начнет двигаться под углом bк оси Ox
. (8)
Закон сохранения импульса в проекции на оси координат Ox и Oy принимает вид:
на ось Ox: 
,
на ось Oy: 
.
С учетом (6)–(8) закон сохранения импульса принимает вид:
| (9) |
,
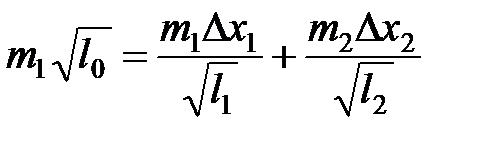на ось Oy 0 = 
.
При этом величины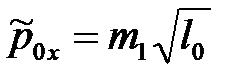 
,
, (10*)
соответственно пропорциональны проекции импульса системы тел на координатную ось Ox до взаимодействия, проекции импульса системы тел на координатную ось Ox после взаимодействия и проекции импульса системы тел на координатную ось Oy после взаимодействия.
До взаимодействия кинетическая энергия системы 
, (10)
а после взаимодействия энергия системы:
.(11)
Коэффициент восстановления энергии
. (12)
|
|
Порядок выполнения работы
Задача1. Сравнение импульсов и энергий тел до и после взаимодействия
1. Выберите два тела приблизительно одинаковой массы, определите их массы m 1 и m 2и запишите в табл. 1.
2. Определите скорость тела 1 при свободном движении. Для этого взведите пружинный механизм, зафиксировав его в первом пазу. Шайбу 1 вставьте в направляющие до упора. Запишите еёначальные координаты(см. рис. 2).Произведите выстрел и занесите в табл.1 координату х крайней точки шайбы.
Таблица 1
| Начальные координаты и массы тел |
 = (кг)
х 01 = (мм)
у 01 = (мм)
|
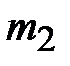 = (кг)
х 02 = (мм)
у 02 = (мм)
| ||||||
| Конечные координаты тел | ||||||||
| при свободном движении | после взаимодействия | |||||||
| № п.п. | х, мм | х 1, мм | у 1, мм | х 2, мм | у 2, мм | |||
| Среднее | 
| 
| 
| 
| 
| |||
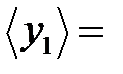
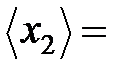
Приращение
координаты
| 
| 
| 
| 
| 
| |||
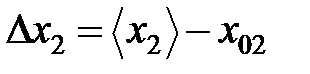
| Расстояние | l 0 = D x | 
| 
| |||||
3. При тех же условиях повторить опыт еще 6 раз. Результаты занесите в табл. 1и рассчитайте среднее значение 
и расстояние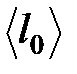 
(1).
4. Установите тело 1 в исходное положение. Тело 2 установите в одном из закрашенных кругов. Запишите начальные координаты крайних точек второго тела (рис.2). Произведите выстрел и занесите в табл.1 координаты крайних точек тел.
5. При тех же условиях повторите опыт еще 6 раз. Результаты занесите в табл.1. Рассчитайте средние значения 
; приращения координат D х 1, D у 1,D х 2, D у 2 и перемещения тел 
и 
.
6. Рассчитайте по формуле (9) величины, пропорциональные проекциям импульсов тел на оси координат до и после соударения, и занесите результаты в табл.2.
Таблица 2
| Импульс | Доудара | Послеудара |
| Вдоль оси Х | 
|  , 
|
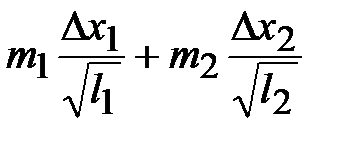| Вдоль оси У |  ,
| |
7. Сравните результаты и сделайте выводы.
8. Рассчитайте величины, пропорциональные энергиям до и после соударения (см. формулы (10 и 11)) и занесите результаты в табл. 3.
Таблица 3
| Энергия | Доудара | Послеудара |
| 
| |
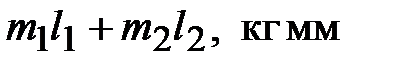
| Коэффициент восстановления |  =
|
9. Сделайте выводы.
10. Повторите опыт по пп.1–9 для тел разной массы. Результаты занесите в таблицы, аналогичные табл. 1–3.
З а д а н и е2. Простейшая оценка погрешности измерений
В качестве систематической погрешности в данных опытах следует взятьприборную погрешность, равную цене деления измерительного прибора.
Случайная погрешность определяется по разбросу выборки:
,
где х max и х min– максимальное и минимальное значение измеряемой величины в серии из N повторных измерений. Этой границе доверительного интервала, совпадающего с , соответствует доверительная вероятность
.
1. В табл. 4 занесите средние значения прямых измерений, выполненных в одном из упражнений и значения погрешностей этих величин – систематической и случайной.
Таблица 4
| Величина | Значение | Абсолютная погрешность | Наибольшая из них | ||
| систематич. S
| cлучайная
| абсолют.
| относит.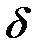 
| ||
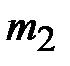| (кг)
| –– | ||||
 (кг)
| –– | ||||
| х 01 (мм) | –– | ||||
| у 01 (мм) | –– | ||||
| х 02 (мм) | –– | ||||
| у 02 (мм) | –– | ||||
| х 1 (мм) | |||||
| у 1 (мм) | |||||
| х 2 (мм) | |||||
| у 2 (мм) |
2. Для каждой величины выберете наибольшую из погрешностей, рассчитанных в п.1 и определите наибольшую относительную погрешность δ измерения каждой величины. В окончательном выводе следует отметить для каких величин желательно увеличить (и как?) точность измерений, а для каких её можно и уменьшить без ущерба для конечного результата.
3. Погрешность измерения величины импульса и энергии в первом приближении можно считать равной (во всяком случае не выше) относительной погрешности менее точно измеренной величины (в табл. 4). С учетом этого сделайте вывод о выполнении законов сохранения импульса и энергии либо о причинах их невыполнении в проведенных опытах и степени упругости ударов.