Материалы к Интернет – тестированию
Дисциплина: Физика
Специальность: 280402.65 – «Природоохранное обустройство территорий»
ДЕ 2. МОЛЕКУЛЯРНАЯ (СТАТИСТИЧЕСКАЯ) ФИЗИКА И ТЕРМОДИНАМИКА (4 задания)
2.1. Распределения Максвелла и Больцмана
 2.1.1. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где
2.1.1. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от  до
до  в расчете на единицу этого интервала.
в расчете на единицу этого интервала.
Для этой функции верными являются утверждения …

| с увеличением температуры максимум кривой смещается вправо |

| площадь заштрихованной полоски равна доле молекул со скоростями в интервале от  до до 
|
| с ростом температуры значение максимума функции увеличивается | |
| с ростом температуры площадь под кривой увеличивается |
Решение: Из определения функции распределения Максвелла следует, что выражение  определяет долю молекул, скорости которых заключены в интервале скоростей от
определяет долю молекул, скорости которых заключены в интервале скоростей от  до
до  (на графике – площадь заштрихованной полоски). Тогда площадь под кривой равна
(на графике – площадь заштрихованной полоски). Тогда площадь под кривой равна 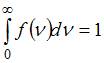 и не изменяется при изменении температуры. Из формулы наиболее вероятной скорости
и не изменяется при изменении температуры. Из формулы наиболее вероятной скорости 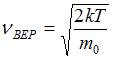 (при которой функция
(при которой функция  максимальна) следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
максимальна) следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
2.1.2. В трех сосудах находятся газы, причем для температур и масс молекул газов имеют место следующие соотношения:  ,
,  На рисунке схематически представлены графики функций распределения молекул идеального газа по скоростям (распределение Максвелла) для этих газов, где
На рисунке схематически представлены графики функций распределения молекул идеального газа по скоростям (распределение Максвелла) для этих газов, где  – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от  до
до  в расчете на единицу этого интервала:
в расчете на единицу этого интервала:

Для графиков этих функций верными являются утверждения, что …

| кривая 1 соответствует распределению по скоростям молекул газа в сосуде 2 |

| кривая 3 соответствует распределению по скоростям молекул газа в сосуде 1 |
| кривая 2 соответствует распределению по скоростям молекул газа в сосуде 2 | |
| кривая 3 соответствует распределению по скоростям молекул газа в сосуде 3 |
Решение: 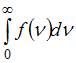 имеет смысл площади, ограниченной кривой распределения и осью абсцисс, и численно равен доле молекул, скорости которых имеют всевозможные значения от 0 до
имеет смысл площади, ограниченной кривой распределения и осью абсцисс, и численно равен доле молекул, скорости которых имеют всевозможные значения от 0 до  . Так как этому условию удовлетворяют все
. Так как этому условию удовлетворяют все  молекул, то
молекул, то  и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости 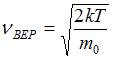 , при которой функция
, при которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. При увеличении массы молекул значение наиболее вероятной скорости уменьшается, следовательно, максимум функции сместится влево и высота максимума увеличится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. При увеличении массы молекул значение наиболее вероятной скорости уменьшается, следовательно, максимум функции сместится влево и высота максимума увеличится.
2.1.3. В трех одинаковых сосудах при равных условиях находится одинаковое количество водорода, гелия и азота

На рисунке представлены графики функций распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от  до
до  в расчете на единицу этого интервала.
в расчете на единицу этого интервала.
Для этих функций верными являются утверждения, что …
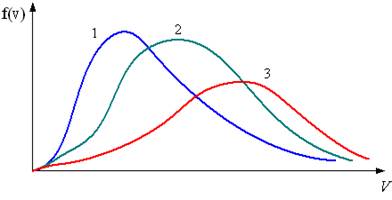

| кривая 1 соответствует распределению по скоростям молекул азота |

| кривая 3 соответствует распределению по скоростям молекул водорода |
| кривая 1 соответствует распределению по скоростям молекул гелия | |
| кривая 2 соответствует распределению по скоростям молекул азота |
Решение: Функция Максвелла имеет вид 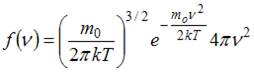 .
.
Полная вероятность равна: 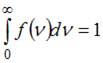 , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости  , при которой функция
, при которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится. Наибольшая масса молекул у азота, меньше у гелия и еще меньше у водорода.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится. Наибольшая масса молекул у азота, меньше у гелия и еще меньше у водорода.
 2.1.4. Зависимости давления p идеального газа во внешнем однородном поле силы тяжести от высоты h для двух разных температур представлены на рисунке.
2.1.4. Зависимости давления p идеального газа во внешнем однородном поле силы тяжести от высоты h для двух разных температур представлены на рисунке.
Для этих функцийверными являются утверждения, что …

| температура T 1 ниже температуры T 2 |

| зависимость давления идеального газа от высоты определяется не только температурой газа, но и массой молекул |
| температура T 1 выше температуры T 2 | |
| давление газа на высоте h равно давлению на «нулевом уровне» (h =0), если температура газа стремится к абсолютному нулю |
Решение: Зависимость давления идеального газа от высоты h для некоторой температуры T определяется барометрической формулой: 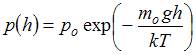 , где
, где 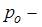 давление на высоте h =0,
давление на высоте h =0,  масса молекулы,
масса молекулы,  ускорение свободного падения,
ускорение свободного падения,  постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура T. Давление
постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура T. Давление 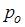 определяется весом всего газа и не меняется при изменении температуры.
определяется весом всего газа и не меняется при изменении температуры.
 2.1.5. На рисунке представлены графики функций распределения молекул идеального газа
2.1.5. На рисунке представлены графики функций распределения молекул идеального газа  во внешнем однородном поле силы тяжести от высоты
во внешнем однородном поле силы тяжести от высоты  для двух разных газов, где
для двух разных газов, где  массы молекул газа (распределение Больцмана).
массы молекул газа (распределение Больцмана).
Для этих функций верными являются утверждения, что …

| масса  больше массы больше массы 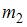
|

| концентрация молекул газа с меньшей массой на «нулевом уровне» (h =0) меньше |
масса  меньше массы меньше массы 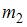
| |
| концентрация молекул газа с меньшей массой на «нулевом уровне» (h =0) больше |
Решение: Зависимость концентрации молекул идеального газа от высоты h для некоторой температуры  определяется распределением Больцмана:
определяется распределением Больцмана: 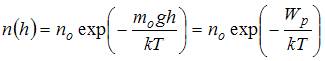 , где
, где  концентрация молекул на высоте h =0,
концентрация молекул на высоте h =0,  масса молекулы,
масса молекулы,  ускорение свободного падения, k - постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул
ускорение свободного падения, k - постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул  , и уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» (h =0) уменьшается, а на высоте h увеличивается.
, и уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» (h =0) уменьшается, а на высоте h увеличивается.
2.1.6. Зависимость давления от высоты для изотермической атмосферы описывается барометрической формулой 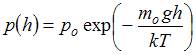 . Для этой зависимости справедливы следующие утверждения …
. Для этой зависимости справедливы следующие утверждения …

| зависимость давления p (h) одного и того же газа при двух разных температурах (T 2> T 1) представлена на рисунке:

| зависимость давления p (h) одного и того же газа при двух разных температурах (T 2> T 1) представлена на рисунке:
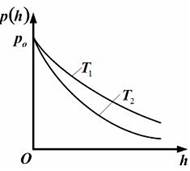
| |

| зависимость p (h) определяется не только температурой газа, но и массой его молекул | с понижением температуры давление газа на высоте h стремится к давлению на высоте h =0 |
2.1.7. Формула 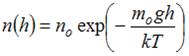 описывает распределение одинаковых молекул массой
описывает распределение одинаковых молекул массой  по высоте в изотермической атмосфере; здесь
по высоте в изотермической атмосфере; здесь  – концентрация молекул при h =0,
– концентрация молекул при h =0,  – их концентрация на высоте h. Для этой зависимости справедливы следующие утверждения …
– их концентрация на высоте h. Для этой зависимости справедливы следующие утверждения …

| приведенные на рисунке кривые соответствуют распределениям для одного и того же газа при разных температурах, причем T 2> T 1:

| приведенные на рисунке кривые соответствуют распределениям для одного и того же газа при разных температурах, причем T 2< T 1:

| |

| приведенные на рисунке кривые соответствуют распределениям для двух разных газов при одинаковой температуре, причем массы молекул удовлетворяют соотношению m 1> m 2:

| приведенные на рисунке кривые соответствуют распределениям для двух разных газов при одинаковой температуре, причем массы молекул удовлетворяют соотношению m 1< m 2:

|
Решение: Зависимость концентрации молекул идеального газа от высоты h для некоторой температуры  определяется распределением Больцмана:
определяется распределением Больцмана:  , где
, где  концентрация молекул на высоте h =0,
концентрация молекул на высоте h =0,  масса молекулы,
масса молекулы,  ускорение свободного падения,
ускорение свободного падения,  постоянная Больцмана. Из формулы следует, что концентрация газа уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, вследствие теплового движения более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» (h =0) меньше, чем для более тяжелых молекул (при одинаковом общем количестве молекул). Для молекул, имеющих бόльшую массу, скорость изменения концентрации выше. С другой стороны для одного и того же газа чем выше температура, тем выше интенсивность хаотического теплового движения, и концентрация молекул газа на «нулевом уровне» (h =0) меньше концентрации тех же молекул при более низкой температуре. При этом скорость уменьшения концентрации при увеличении высоты при боле высокой температуре ниже, то есть экспоненциальный спад более пологий.
постоянная Больцмана. Из формулы следует, что концентрация газа уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, вследствие теплового движения более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» (h =0) меньше, чем для более тяжелых молекул (при одинаковом общем количестве молекул). Для молекул, имеющих бόльшую массу, скорость изменения концентрации выше. С другой стороны для одного и того же газа чем выше температура, тем выше интенсивность хаотического теплового движения, и концентрация молекул газа на «нулевом уровне» (h =0) меньше концентрации тех же молекул при более низкой температуре. При этом скорость уменьшения концентрации при увеличении высоты при боле высокой температуре ниже, то есть экспоненциальный спад более пологий.