Принципиальные схемы систем позволяют анализировать систему с точки зрения функций, выполняемых отдельными элементами, или явлений, положенных в основу принципа действия элементов. Но такие схемы не позволяют исследовать динамические свойства системы. В связи с этим введено понятие структурной схемы системы. Структурной схемой САУ называется условно-графическое изображение системы в форме прямоугольников, соединенных между собой линиями связи со стрелками, указывающими направление прохождения сигнала. Внутри прямоугольников вписываются передаточные функции элементарных динамических звеньев.
Под элементарным динамическим звеном понимают звено, движение которого описывается дифференциальным уравнением не выше второго порядка. Любую систему можно представить конечным числом элементарных звеньев, причем число видов элементарных динамических звеньев также конечно.
Рассмотрим теперь, какому же числу видов элементарных динамических звеньев эквивалентна система, описываемая передаточной функцией n -го порядка:
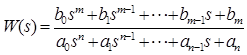. (2.58)
Пусть известны все корни числителя γ k и знаменателя λ i передаточной функции, тогда по теореме Безу можно записать так:
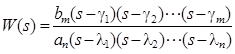. (2.59)
Предположим, что числитель и знаменатель имеют n нулевых корней (неодновременно), hи m – действительных, а остальные корни (m- n - h) и (m- n - m) – комплексно-сопряженные соответственно для числителя и знаменателя. Преобразуем сомножители числителя и знаменателя, соответствующие вещественным корням λ i =-s i, g k =-r k и комплексно-сопряженным корням l r,r +1=-a r ± j b r; g q,q +1= - a q ± j b q к такому виду:
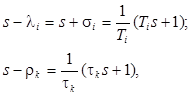
где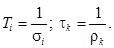 
Для комплексно-сопряженных корней знаменателя имеем:
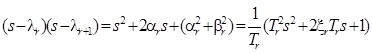
Здесь a r и b r – соответственно вещественная и мнимая части корня
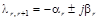, a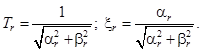 
Аналогично можно записать для сомножителей числителя
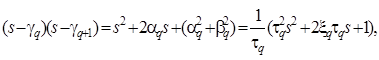
где
.
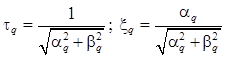На основании сделанных преобразований можно представить выражение (2.58) в следующей форме:
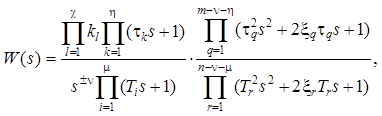(2.60)
где kl – вещественные числа, получаемые в результате производимых преобразований выражений (2.58) и (2.59) при вынесении множителей за скобки.
В соответствии с полученной формой выражения для передаточной функции можно указать следующие типы элементарных динамических звеньев:
1) Усилительное (безынерционное) звено.
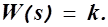
2) Идеальное дифференцирующее звено.
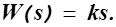
3) Идеальное интегрирующее звено.
4) Апериодическое или инерционное звено.
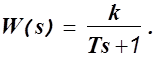
5) Колебательное звено.
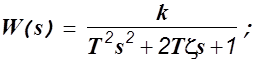
а) колебательное звено при 0<z<1;
б) апериодическое звено второго порядка при z>1;
в) консервативное звено при z=0.
6) Форсирующее звено первого порядка.
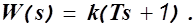
7) Форсирующее звено второго порядка.
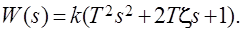
Рассмотренные 7 элементарных звеньев относятся к звеньям минимально-фазового типа, которые имеют отрицательные значения корней. Такие звенья являются устойчивыми, поскольку корни располагаются в левой плоскости корней. Наряду с минимально-фазовыми звеньями существуют нелинимально-фазовые звенья. Это неустойчивые звенья, поскольку корни полинома являются положительными. Передаточные функции неминимально-фазовых звеньев имеют такую же математическую структуру, как и минимально-фазовые звенья, но отличаются от последних тем, что знак при свободном члене для звеньев первого порядка или при слагаемом, содержащим s в первой степени, будут отрицательным.
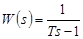- апериодическое звено неминимально-фазового типа
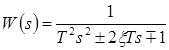- колебательное звено неминимально-фазового типа.
В случае описания линейных систем с распределенными параметрами или с запаздыванием, относящихся к классу особых линейных систем, возникает необходимость введения звена с чистым запаздыванием с передаточной функцией вида W (s)= e-s τ, где t – время запаздывания.
Рассмотрим более подробно свойства элементарных динамических звеньев, относящихся к звеньям минимально-фазового типа.