Кунсбаева Гульназ Абдулхаковна
Сибай – 2017
Оглавление
ВВЕДЕНИЕ. 3
ГЛАВА I. ПОНЯТИЯ.. 4
ГЛАВА II. РАВНОВЕСНОЕ ПРОИЗВОДСТВО. 6
ГЛАВА III. ЗАДАЧИ.. 7
ЗАДАЧА 1. 7
ЗАКЛЮЧЕНИЕ. 24
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 25
ВВЕДЕНИЕ
Математические методы являются важнейшим инструментом анализа экономических явлений и процессов, построения теоретических моделей, позволяющих отобразить существующие связи в экономической жизни, прогнозировать поведение экономических субъектов и экономическую динамику. Математическое моделирование становится языком современной экономической теории, одинаково понятным для учёных всех стран мира.
Человеку, чтобы сохранять себя, нужна, совокупность материальных условий и благ. Все блага, необходимые человеку, делятся на 2 группы. Первая группа – блага, которые могут быть усвоены без каких-либо усилий. Эти блага находятся в среде человеческого обитания и пригодны к употреблению без переработки. Вторая группа – блага, которые человек не может себе доставить просто так. Получение этих благ требует усилий с его стороны, и надо совершать определенные действия, чтобы их стало больше. Например, разведение пчел и производство меда.
Вторая группа благ отличается от первой тем, что прежде чем потребить в необходимом количестве, их надо произвести. Эти производимые блага называются экономическими. Именно производство – исходный пункт всех наших дальнейших рассуждений. Изготовление материальных благ и услуг при котором цена товара такова, что рынок находится в равновесном состоянии.
В данной курсовой даны такие понятия как производство, экономика-математические модели, товар, спрос и предложение. Также отражена взаимосвязь спроса и предложения.
|
|
ГЛАВА I. ПОНЯТИЯ
Экономико-математическая модель - математическое описание экономического процесса или объекта, произведенное в целях их исследования и управления ими: математическая запись решаемой экономической задачи (поэтому часто термины “модель” и “задача” употребляются как синонимы). Существует еще несколько вариантов определения этого термина.
В самой общей форме модель - условный образ объекта исследования, сконструированный для упрощения этого исследования. При построении модели предполагается, что ее непосредственное изучение дает новые знания о моделируемом объекте (см. Моделирование). Все это полностью относится и к экономико-математическая модель.
В принципе в экономике применимы не только математические (знаковые), но и материальные модели. Например, гидравлические (в которых потоки воды имитируют потоки денег и товаров, а резервуары отождествляются с такими экономическими категориями, как объем промышленного производства, личное потребление и др.) и электрические (в США была известна модель «Эконорама», представлявшая собой сложную электрическую схему, в которой имитировались экономические процессы). Но все эти попытки имели лишь демонстрационное применение, а не служили средством изучения закономерностей экономики. С развитием же электронно-вычислительной техники потребность в них, по-видимому, и вовсе отпала.
Экономико-математическая модель оказывается в этих условиях основным средством модельного исследования
|
|
экономики. Модель может описывать либо внутреннюю структуру объекта,
либо, если структура неизвестна, — его поведение, т.е.реакцию на воздействие известных факторов (принцип «черного ящика«). Один и тот же объект может быть описан различными моделями в зависимости от исследовательской или практической потребности, возможностей математического аппарата и т.п. Поэтому всегда необходима оценка модели и области, в которой выводы из ее изучения могут быть достоверны.
Во всех случаях необходимо, чтобы модель содержала достаточно детальное описание объекта, позволяющее, в частности, осуществлять измерение экономических величин и их взаимосвязей, чтобы были выделены факторы, воздействующие на исследуемые показатели. Например, формула, по которой определяется на заводе потребность в материалах, исходя из норм расхода экономико-математической модели.
Производство, в экономическом смысле — процесс создания какого-либо продукта.
Понятие производства характеризует специфически человеческий тип обмена веществами с природой, или, более точно — процесс активного преобразования людьми природных ресурсов в какой-либо продукт. Как отмечает Философская энциклопедия, процесс производства всегда носит общественный характер: производство обособленного одиночки вне общества представляет собой, по выражению Маркса, такую же бессмыслицу, как развитие языка без совместно живущих индивидов.
Современное общественное производство включает в себя не только материальное производство, но и также нематериальную сферу — производство нематериальных благ и услуг (новые научные открытия, технические изобретения, народное образование, культура, искусство, здравоохранение, бытовое обслуживание, управление, финансирование и кредитование, спорт и др.). Развитие нематериального производства и сферы услуг в решающей степени зависит от производства материальных благ — его технической оснащённости и величины выработки.
|
|
Спрос — это зависимость между ценой и количеством товара, который покупатели могут и желают купить по строго определенной цене, в определенный промежуток времени. Платежеспособная потребность, подтвержденная деньгами и «выведенная» на рынок. Спрос на товар показывает на то количество товара, которое потребитель готов приобрести в данный момент, по определенной цене.
Товар - любая вещь, которая участвует в свободном обмене на другие вещи; продукт, произведённый для продажи.
Продукты, производимые не для обмена, в экономическом смысле товарами не являются.
Предложение - понятие, отражающее поведение товаропроизводителя на рынке, его готовность произвести (предложить) какое-либо количество товара за определённый период времени при определённых условиях.
ГЛАВА II. РАВНОВЕСНОЕ ПРОИЗВОДСТВО.
Под равновесным производством экономико – математические модели которых мы рассмотрим подразумиваются равновесный объём производства представляет собой такой объём ВВП, при котором произведённый продукт равен объёму потреблённых товаров и услуг, то есть совокупным расходам.
Равновесный объем производства (выпуска) - это такой объем производства, при котором совокупное предложение равно совокупному спросу, или это объем производства, обеспечивающий расходы, достаточные для закупки данного объема производства.
AS (GDP) = Y = AD.
При рассмотрении модели "совокупный спрос - совокупное предложение" (модель AD-AS) равновесный объем производства графически определялся в точке пересечения кривых совокупного спроса и совокупного предложения. В рассматриваемой нами стандартной кейнсианской модели совокупного спроса цены предполагаются неизменными, поэтому нет необходимости включать их в график равновесного выпуска продукции.
Используется другой способ изображения равновесного объема производства, так называемый кейнсианский крест. Это способ с применением биссектрисы, то есть линии под углом 450 (см. рис. 8.6). Особенность этой прямой состоит в том, что любая точка на ней предполагает равенство значений переменных, расположенных на горизонтальной и вертикальной осях координат. В точке пересечения линии совокупного спроса с биссектрисой и будет определен равновесный объем производства, так как именно этому объему соответствует такой же уровень совокупного спроса. Это точка Е. Равенство выпуска и совокупных расходов в точке Е выполняется.

ГЛАВА III. ЗАДАЧИ
ЗАДАЧА 1
УСЛОВИЯ ЗАДАЧИ
Цех предприятия производит два вида изделий А и В, для изготовления которых требуются ресурсы трех видов R1, R2, R3. Данные о наличии ресурсов, количество ресурсов каждого вида, необходимое для изготовления тысячи изделий А и В (нормы расхода), а также прибыль, получаемая от реализации тысячи изделия каждого вида, приведены в табл. 1.1. Определить оптимальные объемы производства каждого вида изделий за плановый период, обеспечивающие максимальную прибыль предприятию.
Таблица 1.1
| Виды ресурсов | Наличие | Нормы расхода | |
| Тип А | Тип В | ||
| R1 | |||
| R2 | 2,5 | ||
| R3 | 1,2 | ||
| Прибыль от продажи |
ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Пусть за плановый период выпускается Х1 (тыс. шт.) изделий А и Х2 (тыс. шт.) изделий В. По условию задачи (табл.1) прибыль, получаемая от реализации 1000 шт. изделий А, составляет 15 (уел. ед.), а 1000 шт. изделий В - 16 (усл.ед.).
Тогда прибыль, получаемая от реализации Xt (тыс. шт.) изделий А и Х2 (тыс. шт.) изделий В, выпущенных за плановый период, может быть записана в виде выражения Z= 15 Х1+16Х2.
Отрицательные значения Х1 и Х2 не имеют смысла, то есть Х1 >=0, Х2 >=0.
Величины Х1 и Х2 нельзя выбирать произвольно, так как на них накладываются ограничения, определяемые наличием ресурсов R1, R2, R3. Как видно из табл. 1, для изготовления тыс. шт. изделий А требуется 10 (ед.) ресурса R1, а для изготовления тыс. шт. изделий В - 5 (ед.) ресурса R1. Следовательно, расход ресурса R1 для выпуска Х1 (тыс.шт.) изделий А составит 10 Х1 (ед.), а для выпуска Х2 (тыс. шт.) изделий В - 5Х2 (ед.). Таким образом, для планового выпуска деталей А и В потребуется 10 Х1+ 5Х2 (ед.) ресурса R1. В связи с тем, что запас ресурса R1 составляет 200 (ед.), ограничение по нему будет иметь вид: 10 Х1 + 5Х2, <= 200;
Аналогично рассуждая, можно составить ограничения для ресурсов R2 и R3: R2: 2,5Х1 + 5Х2<= 100;
R3: 2 Х1 + 1,2Х2<= 60.
Получили математическую модель задачи.
Имеем целевую функцию линейной формы:
Z = 15Xi + 16Х2 —> шах (1)
систему линейных ограничений:
10 Х1 + 5Х2, <= 200
2,5Х1 + 5Х2<= 100 (2)
2 Х1 + 1,2Х2<= 60
и граничные условия: X, >= 0, Х2 >=0 (3)
Задача формулируется следующим образом: найти такие неотрицательные значения переменных X, и Х2, которые будут удовлетворять системе ограничений (2) и обращать в максимум целевую функцию (1).
Целевая функция и ограничения имеют линейную форму, поэтому данная задача относится к классу задач линейного программирования и для ее решения можно использовать симплекс-метод. Так как задача имеет только две переменные, она может быть решена графическим методом.
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ
Введем на плоскости прямоугольную систему координат Х1, Х2.
ОПРЕДЕЛЕНИЕ ОБЛАСТИ ДОПУСТИМЫХ РЕШЕНИЙ
Область допустимых решений определяется граничными условиями (3) и системой неравенств (2). Граничные условия Х1 >=0, Х2 >=0 указывают на то, что область допустимых решений находится в 1-м квадранте.
Построим систему неравенств (2). Каждое неравенство геометрически определяет полуплоскость с граничными прямыми
10 Х1 + 5Х2, <= 200
2,5Х1 + 5Х2<= 100 (4)
2 Х1 + 1,2Х2<= 60
Построим эти прямые (рис. 1). Каждая из них делит плоскость на две полуплоскости. Решение следует искать в той полуплоскости, все точки которой удовлетворяют неравенству. Чтобы определить эту полуплоскость, возьмем какую-нибудь точку на плоскости, например точку с координатами (0,0). Если приравнять нулю значения Х1 и Х2 в левой части соответствующих неравенств, получим соотношение 0 <= const, значит точка с координатами (0,0) входит в полуплоскость, соответствующую рассматриваемому неравенству. Во все полуплоскости, соответствующие ограничениям (2) входит начало координат (при Х1=Х2=0 10 Х1 + 5Х2, <= 200, 2,5Х1 + 5Х2<= 100, 2 Х1 + 1,2Х2<= 60). Так как система (2) совместна, то полуплоскости, пересекаясь, образуют общую для всех полуплоскостей часть, которая представляет собой многоугольник. Таким образом, определили область, удовлетворяющую всем ограничениям и граничным условиям, то есть область допустимых решений (многоугольник решений). Известно, что оптимальное решение должно находиться на границе этой области, и, если решение единственное, в одной из ее вершин. Точка с координатами (X1, Х2), в которой значение целевой функции достигает максимума, должна находиться в одной из вершин выделенного многоугольника.
НАХОЖДЕНИЕ ОПТИМАЛЬНОГО РЕШЕНИЯ
Проведем линию уровня целевой функции, проходящую через начало координат:
Z= 15Х1 + 16Х2 = 0.
Значение Z возрастает в направлении нормального вектора п = {15; 16}. Будем передвигать прямую параллельно самой себе в направлении вектора п до тех пор, пока многоугольник решений не будет находиться по одну сторону от нее, и прямая не будет иметь с ним, по крайней мере, одну общую точку. Этой точкой будет точка С с координатами Х1 = 13,3 и Х2= 13,3, в которой целевая функция Z принимает максимальное значение. Подставив значения Х1= 13,3 и Х2= 13,3 в целевую функцию Z= 15Х1 + 16Х2 = 0. Получим ее максимальное значение Z = 15∙13,3+16∙13,3 =413.
Общая прибыль от реализации x1 изделий вида А и x2 изделий вида В составит:
Z=15∙x1+16∙x2→max
Таким образом, мы приходим к решению следующей математической задачи: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция Z принимает максимальное значение.
Решим неравенства, преобразовав их в равенства:
1) 10∙x1+5∙x2=200
x1=0 → x2=40
x2=0 → x1=20
2) 2,5∙x1+5∙x2=100
x1=0 → x2=20
x2=0 → x1=40
3) 2∙x1+1,2∙x2=60
x1=0 → x2=50
x2=0 → x1=30
10∙x1+5∙x2=200
2,5∙x1+5∙x2=100
x1=13,3 (13)
x2=13,3 (13)
Z=15∙13,3+16∙13,3=413
Это оптимальное решение.
(Точность решения задачи будет зависеть от точности построения графика.)
Ответ: max Z =413 при Xt = 13,3, Х2 = 13,3.
ИСПОЛЬЗОВАНИЕ СИМПЛЕКС-МЕТОДА ДЛЯ РЕШЕНИЯ ЗАДАЧИ
Определение базисного (допустимого) решения
10∙x1+5∙x2≤200 10∙x1+5∙x2+x3=200
2,5∙x1+5∙x2≤100 2,5∙x1+5∙x2+x4=100
2∙x1+1,2∙x2≤60 2∙x1+1,2∙x2+x5=60
x1, x2, x3, x4, x5≥0 Z=15∙x1+16∙x2+0∙x3+0∙x4+0∙x5
x3=200-(10∙x1+5∙x2)
x4=100-(2,5∙x1+5∙x2)
x5=60-(2∙x1+1,2∙x2)
Z=0-(-15∙x1-16∙x2-0∙x3-0∙x4-0∙x5)
x1=0, x2=0, x3=200, x4=100, x5=60
1. Из отрицательных элементов последней строки табл.1.2, соответствующих переменным x1 и x2, выберем максимальный по модулю элемент: -16, соответствует x2. Небазисная переменная x2 должна быть введена в базис. 2. Поделим элементы столбца значений базисных переменных на соответствующие положительные коэффициенты выбранного столбца: 200/5=40
100/5=20
60/1,2=50
Запишем частные от деления во вспомогательный столбец б. Выберем элемент, который дает минимальное частное от деления: 20. Минимальное частное 20 соответствует второй строке с базисной переменной x4. Переменная x4 должна быть выведена из базиса.
3. Разделим элементы выбранной строки (второй строки) на разрешающий элемент (5). Результат запишем во вторую строку симплекс-таблицы 9. Построение первой строки симплекс-таблицы 1.3
4. Элементы полученной второй строки симплекс-таблицы 1.3 умножим на коэффициент первого элемента выделенного столбца симплекс-таблицы 1.2 и вычтем из соответствующих элементов первой строки симплекс-таблицы 1.2. Получим первую строку симплекс-таблицы 1.3.
Построение третьей строки симплекс-таблицы 1.3.
5. Элементы полученной второй строки симплекс-таблицы 1.3 умножим на коэффициент третьего элемента выделенного столбца симплекс-таблицы 1.2 и вычтем из соответствующих элементов третьей строки симплекс-таблицы 1.2. Получим третью строку симплекс-таблицы 1.3.
Построение четвертой строки симплекс-таблицы 1.3
6. Элементы полученной второй строки симплекс-таблицы 1.3 умножим на коэффициент четвертого элемента выделенного столбца симплекс-таблицы 1.2 и вычтем из соответствующих элементов четвертой строки симплекс-таблицы 1.2. Получим четвертую строку симплекс-таблицы 1.3. 7. В симплекс-таблице 1.3 проделываются аналогичные операции, что и в симплекс-таблице 1.2. Полученные результаты записываем в симплекс-таблицу 1.4.
Таблица 1.2
| № | Базисные переменные | Значения базисных переменных | Коэффициенты | |||||
| х1 | х2 | х3 | х4 | х5 | б | |||
| х3 | ||||||||
| х4 | 2,5 | |||||||
| х5 | 1,2 | |||||||
| z | -15 | -16 |
Таблица 1.3
| № | Базисные переменные | Значения базисных переменных | Коэффициенты | |||||
| х1 | х2 | х3 | х4 | х5 | б | |||
| х3 | 7,5 | -1 | 13,3 | |||||
| х2 | 0,5 | 0,2 | ||||||
| х5 | 1,4 | -0,24 | 25,7 | |||||
| z | -7 | 3,2 |
Проверим, является ли данное решение допустимым.
Так как в столбце значений базисных переменных все элементы неотрицательные, то полученное решение является допустимым.
Проверка на оптимальность:
целевая функция имеет максимальное значение, так как все коэффициенты в строке целевой функции положительны.
Таблица 1.4
| № | Базисные переменные | Значения базисных переменных | Коэффициенты | ||||
| х1 | х2 | х3 | х4 | х5 | |||
| x1 | 13,33 | 0,1333 | -0,133 | ||||
| x2 | 13,33 | -0,07 | 0,27 | ||||
| x5 | 17,33 | -0,19 | -0,05 | ||||
| z |
Двойственная задача
Исходная задача Двойственная задача
10∙x1+5∙x2≤200 10∙y1+2,5∙y2+2∙y3≥15
2,5∙x1+5∙x2≤100 5∙y1+5∙y2+1,2∙y3≥16
2∙x1+1,2∙x2≤60
x1,x2≥0
Z=15∙x1+16∙x2→max Zд=200∙y1+100∙y2+60∙y3→min
Анализ оптимального решения
При увеличении ресурса Ri: Z=Zопт+yi∙1
При уменьшении ресурса Ri: Z=Zопт-yi∙1
R1: Z=Zопт+1∙1=413+1=414
Z=Zопт-1∙1=413-1=412
R2: Z=Zопт+2∙1=413+2=415
Z=Zопт-2∙1=413-2=411
R3: Z=Zопт+0∙1=413+0=413
Z=Zопт-0∙1=413-0=413
Отчёты по пределам
Z=15∙13,3+16∙13,3=413
Для значения х1 на нижнем пределе:
Z=15∙0+16∙13,3=213
Для значения х2 на нижнем пределе:
Z=15∙13,3+16∙0=200
РЕШЕНИЕ ЗАДАЧИ В EXCEL
Для решения задачи составьте электронную таблицу, отражающую ее математическую модель (рис. 2, 3). На рис. 2 показана электронная таблица в режиме отображения вычислений (исходное состояние), на рис. 3 - в режиме отображения формул. На рисунках введено сокращение: ЦФ - целевая функция.
Рис. 2

Рис. 3
| переменные | х1 | х2 | |||
| значение | |||||
| цф | |||||
| коэф вцф | =СУММПРОИЗВ(B3:C3;B5:C5) | ||||
| ресурсы | левая часть | знак | правая часть | ||
| R1 | =СУММПРОИЗВ($B$3:$C$3;B8:C8) | ≤ | |||
| R2 | 2,5 | =СУММПРОИЗВ($B$3:$C$3;B9:C9) | ≤ | ||
| R3 | 1,2 | =СУММПРОИЗВ($B$3:$C$3;B10:C10) | ≤ |
Работа в диалоговом окне «Поиск решения»
Для подготовки к решению задачи оптимизации выполните команду: Сервис - Поиск решения. На экране появится диалоговое окно Поиск решения (рис. 4). Выполните следующие действия:
1.В поле Установить целевую ячейку введите адрес $D$5.
2.Для выбора направления изменения целевой функции установите переключатель в положение Максимальному значению.
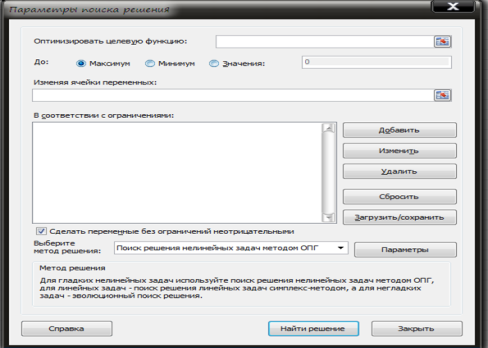
Рис. 4
В поле Изменяя ячейки введите адрес блока ячеек $В$3: $С$3.
4.Введите граничные условия и ограничения: щелкните по кнопке Добавить. На экране появится диалоговое окно Добавление ограничения. Для ввода граничных условий Х1чХ2 > 0 в поле Ссылка на ячейку введите левую часть отношения (B3:СЗ), в следующее поле - его знак (≥), в последнее поле введите правую часть ограничения - 0. Щелкните по клавише Добавить. На экране появится диалоговое окно Добавление ограничения. Введите ограничения по ресурсам: D8:D10 ≤ F8:F10 аналогичным образом и щелкните по кнопке ОК. На экране появится диалоговое окно Поиск решения с введенными ограничениями (рис. 5).
Решение задачи Решение задачи будем производить в диалоговом окне Поиск решения. В нем выполните следующие действия:
1.Щелкните по кнопке Параметры. Появится диалоговое окно Параметры поиска решения (рис. 6).
2.Установите Максимальное время решения задачи (оставьте предлагаемое по умолчанию - 100 с), Предельное число итераций (оставьте предлагаемое по умолчанию - 100).
3.Установите флажок Линейная модель.
4.Нажмите ОК. Появится диалоговое окно Поиск решения.
5.Щелкните по кнопке Выполнить. Появится диалоговое окно Результаты поиска решения (рис.7).

Рис. 5

Рис. 6

Рис. 7
5. В окне Результаты поиска решения в поле Тип отчета выделите названия всех трех отчетов: Результаты, Устойчивость, Пределы. В рабочей книге появятся три новых листа с их именами.
6. Закройте окно, нажав ОК. На экране появится исходная таблица с результаты решения задачи (рис. 8): в блоке ячеек ВЗ:СЗ - значения переменных Х1-Х2 (Х1=13,33, Х2=13,33), в ячейке D5 - максимальное значение целевой функции (413,33).
Результаты решения в Excel совпадают с результатами, полученными при решении задачи графическим методом и симплекс-методом.

Рис. 8
Анализ оптимального решения задачи в Excel
Отчет по результатам
Щелкните мышью по ярлычку Отчет по результатам. На экране появится лист данного отчета (рис. 9).
В верхней таблице отчета указан номер ячейки - $D$5 (целевой ячейки), в которой находится значение целевой функции, исходное, равное 0, и результирующее - максимальное значение целевой функции – 413,33, полученное в результате решения задачи оптимизации.
В средней таблице отчета располагаются номера ячеек, в которых находятся значения искомых переменных Х1 и Х2, исходные (равные нулю) и результирующие значения (соответственно 13,33 и 13,33), при которых целевая функция достигает максимального значения.

Рис. 9
В нижней таблице представлены номера ячеек, в которых записаны значения левых частей ограничений, полученные после решения задачи оптимизации (требуемое количество ресурсов каждого вида, необходимое для получения максимального значения целевой функции). В столбце Разница приводятся данные о разности между значениями левых частей ограничений, полученных в результате решения задачи (требуемым количеством ресурсов), и правых частей ограничений (имеющимся количеством ресурсов), другими словами, данные о количестве неиспользованного ресурса каждого вида. Если разность равна нулю (ресурс используется полностью), то в соответствующей ячейке столбца Статус указывается связанное, если разность не равна нулю (ресурс используется не полностью), в соответствующей ячейке столбца Статус записано не связанное.
Ниже приводятся номера ячеек, в которых располагаются значения искомых переменные Х1 и Х2 и их значения, при которых целевая функция достигает максимального значения.
Отчет по устойчивости
Щелкните мышью по ярлычку Отчет по устойчивости. На экране появится лист данного отчета (рис. 10).
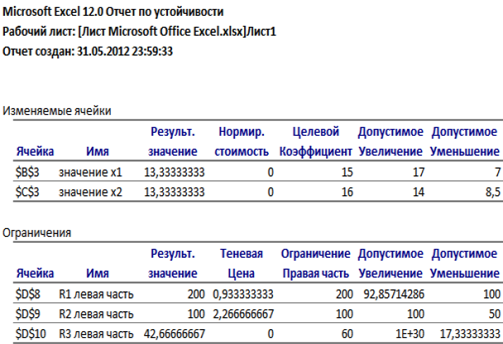
Рис. 10
В нем приводятся данные о чувствительности целевой ячейки к изменению ограничений. Отчет состоит из двух таблиц: Изменяемые ячейки и Ограничения.
В таблице Изменяемые ячейки выводятся номера ячеек, в которых находятся искомые переменные Х1 и Х2 и их значения, при которых целевая функция достигает максимума.
В столбце Целевой коэффициент приводятся значения коэффициентов при изменяемых переменных Х1 и Х2 в выражении целевой функции.
Столбцы Допустимое увеличение и Допустимое уменьшение
характеризуют пределы, в которых могут изменяться эти коэффициенты, без изменения найденного оптимального решения.
В таблице Ограничения содержится информация об ограничениях, накладываемых на оптимизируемые переменные.
В столбце Результирующие значения указаны данные о потребности в ресурсах для оптимального решения.
Данные столбца Теневая цена характеризуют изменение значения целевой функции (Z) при увеличении на единицу значения соответствующего ограничения (для ресурсов R1, R2, R3), т.е. двойственные оценки (Y1 Y2, Y3)
Столбцы Допустимое увеличение и Допустимое уменьшение характеризуют пределы, в которых могут изменяться объемы изменяющихся ресурсов, если не изменять оптимального набора переменных, входящих в оптимальное решение.
Отчет по пределам
Щелкните по ярлычку Отчет по пределам. Появится окно отчета (рис. 11).

Рис. 11
В нем приводится оптимальное значение целевой функции и соответствующие ему значения переменных Х1 и Х2, а также нижний и верхний пределы их изменения, при которых не нарушаются ограничения модели. Например,
Z= 15Х1 + 16Х2 = 15Ч13,33 + 16Ч13,33 = 76,7+ 73,3 = 413,3 - оптимальное решение.
ЗАКЛЮЧЕНИЕ
В данной курсовой работе мы изучили равновесное производство, экономические термины. Рассмотрели задачу, построили математическую модель и решили задачу в Excel.
В дополнение хочется сказать, математические методы являются важнейшим инструментом анализа экономических явлений и процессов, построения теоретических моделей, позволяющих отобразить существующие связи в экономической жизни, прогнозировать поведение экономических субъектов и экономическую динамику.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Бункина М. К. Семенов В. А.: Макроэкономика, 1996.
2. Электронная книга экономико математические модели и методы
3. Белых, Андрей Акатович.
История советских экономико-математических исследований
4. Официальный сайт ru.wikipedia.org
5. Официальный сайт dic.academic.ru
6. Сайт knigi.news