Разветвляющиеся алгоритмы
Цель: Освоить навык составления блок-схем алгоритмов разветвляющегося типа.
Задание: Для поставленных задач (согласно своего варианта) написать математическую модель решения задачи, составить таблицу входных и выходных данных, нарисовать блок-схему. Для задачи № 2 необходимо составить 2 блок-схемы: одну с использованием конструкции полная и (или) не полная развилка.
Задача № 1 (по вариантам)
Вычислить значение функции y от произвольного значения аргумента x. Алгоритм вычисления функции задан в таблице 1.
Таблица 1
| Номер задачи | Функция | Условия | Данные | |
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
|
 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
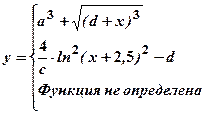
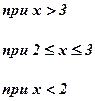
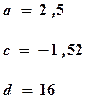
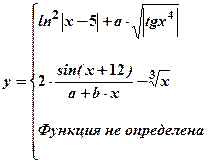
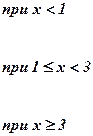
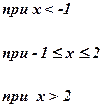
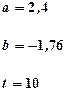
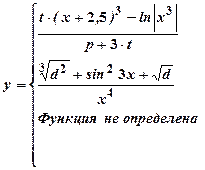
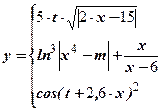
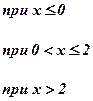
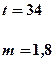
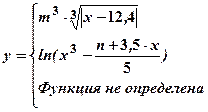
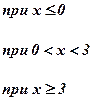
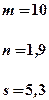
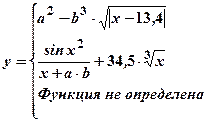
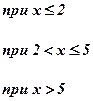
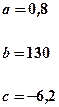
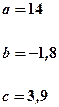
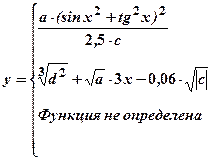
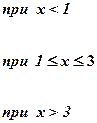
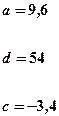
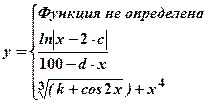
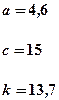
Теоретические сведения
Напомним, что алгоритмизация – это процесс разработки алгоритма (плана действий) для решения задачи.
Есть три основных типа алгоритма: линейный, разветвляющийся и циклический. Темой рассмотрения данной лабораторной работы является разветвляющийся алгоритм.
Разветвляющийся алгоритм содержит проверку некоторого логического условия, в зависимости от выполнения или не выполнения которого вычисления могут пойти по разным направлениям.
Для обозначения блоков разветвляющихся алгоритмов служит конструкция развилка.
Конструкция развилка
Есть несколько вариантов развилки: основная - полная развилка (рис. 1,а); неполная развилка (рис. 1,б), ее еще называют «коррекция» и множественный выбор (рисунок 1,в).
В конструкциях (рис. 1,а и 1,б) L - некоторое логическое выражение, которое может принимать одно из двух значений: «истина», если проверяемое условие верно (на схеме - направление «Да») или «ложь», если проверяемое условие неверно (на схеме - направление «нет»). В зависимости от значения L происходит выбор направления движения по схеме. S, S1, S2 - функциональные блоки.
|
|
Пример логических выражений: a > b; x2 +y2 £ R; a £ t £ b и т.п.
В конструкции на рисунке 1,в под Pi обычно понимается значение какой-либо метки оператора, которому передается управление. В современных алгоритмических языках обязательно есть оператор, позволяющий реализовать эту конструкцию.
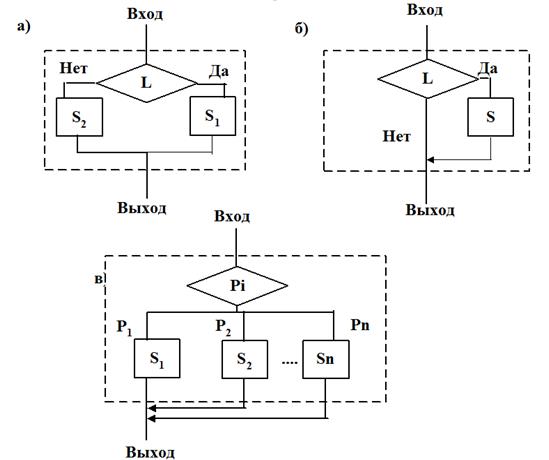
Рисунок 1
Примеры выполнения задания
Задача № 1
Постановка задачи:
Вычислить значение F = 
,
где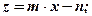 
m, n, x - заданные числа, y вычисляется по одной из формул:
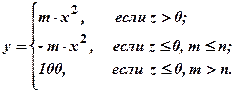
Таблица входных данных
| Переменная | Описание переменной |
| M | Число, задаваемое пользователем |
| X | Число, задаваемое пользователем |
| N | Число, задаваемое пользователем |
Таблица выходных данных
| Переменная | Описание переменной |
| F | Значение функции |
Блок-схема:
Задача № 2
Постановка задачи:
функция y = f(x) задана графически:
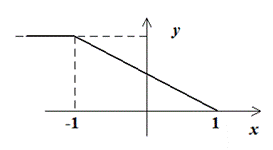
разработать алгоритм, позволяющий определить значения функции для произвольно заданного вещественного х.
Математическая модель:
В данной задаче математическая модель задана в виде графика. Запишем ее в виде формул.
Из графика следует, что вся числовая ось разбита на три части: x< -1, -1£ x £1, x>1.
На полуинтервале x < -1 задана прямая,
паралельная оси х, ее уравнение у = 1.
На интервале -1£ x £1 задана прямая, проходя ходящая через две точки (-1, 1) и (1, 0). Для вычивычисления коэффициентов a и b уравнения
|
|
прямой y = ax + b, решим систему уравнений:
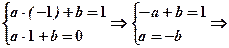
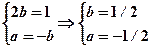
Итак, получено уравнение прямой:
у = -0,5х + 0,5.
Учитывая, что на полуинтервале х>1
функция не определена, математическую модель можно записать так:
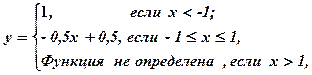
где х - любое вещественное число.
Таблица входных данных
| Переменная | Описание переменной |
| х | Значение аргумента (задается пользователем) |
Таблица выходных данных
| Переменная | Описание переменной |
| Х | Аргумент, заданный пользователем |
| Y | Значение функции при заданном аргументе |
| S | Сообщение «Функция не определена» |
Блок-схема:
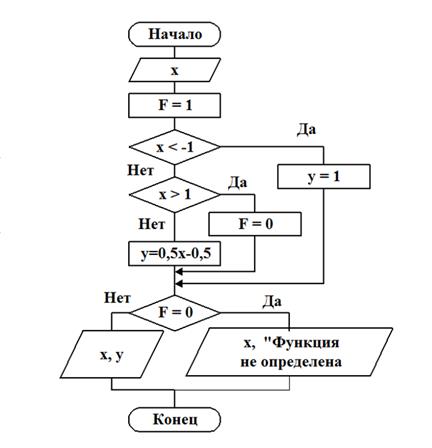
Примечание. в этом алгоритме использовали так называемый «флаг» (переменная F). В качестве «флага» в алгоритмах часто используют переменные, которым программист сам присваивает определенные значения. Эти значения придумываются (оговариваются) заранее и вводятся в соответствующих местах программ по мере необходимости.
В данной задаче принято, что «флаг» F будет принимать значение 1, если функция будет определена и F = 0, если функция не определена.
Задача № 3
Постановка задачи:
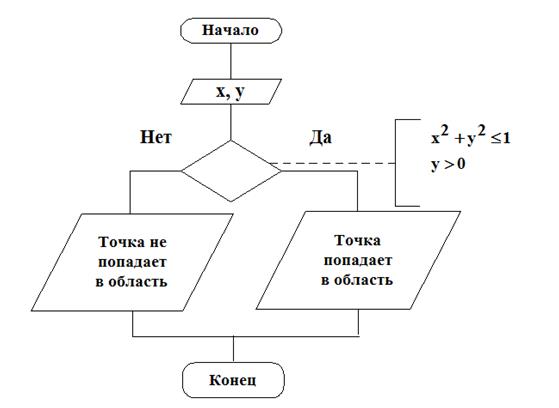
определить, попадает ли точка с произвольными координатами (х, у) в заштрихованную область:
Математическая модель:
Для решения данной задачи надо, учитывая заданную область, записать условие попадания точки в эту область, то есть построить математическую модель.
точка с заданными координатами
(х, у) попадет в заштрихованную область, если эти координаты будут удовлетворять условиям: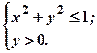 
|
|
Таблица входных данных
| Переменная | Описание переменной |
| Х | Координата заданной точки по оси X |
| Y | Координата заданной точки по оси Y |
Таблица выходных данных
| Переменная | Описание переменной |
| S1 | Сообщение «Точка попадает в область» |
| S2 | Сообщение «Точка не попадает в область» |
Блок-схема:
Контрольные вопросы.
1) Дайте определение алгоритма.
2) Какие виды конструкций развилка вы знаете?
3) Какие основные типы алгоритмов вы знаете?
4) Дайте определение разветвляющегося алгоритма
Требования к оформлению отчета по лабораторной работе:
1 Отчет сдается в распечатанном и в электронном виде.
2 Отчет должен быть выполнен в соответствии с руководящим документом оформления текстовых студенческих работ.
3 В отчете для заданной задачи должны быть приведены:
- постановка задачи
- математическая модель решения задачи
- таблица входных данных
- таблица выходных данных
- блок-схема решения задачи.
4 Файл, содержащий электронную версию отчета должен иметь название в соответствии со следующим шаблоном:
Название группы_Название предмета_ФИО студента_номер лабораторной работы.
Например, для группы 1ПИб-1 для предмета «Информатика» название файла будет выглядеть следующим образом:
ПИб1_Информатика_Иванов А.С._лр5.doc
ПРИЛОЖЕНИЕ А
(обязательное)