Лабораторная работа № 1.06
Определение момента инерции махового колеса и изучение маятника Максвелла
Цель работы: Изучение законов вращательного движения твердых тел. Определение момента инерции махового колеса и силы трения в упоре. Определение момента инерции маятника Максвелла.
Приборы и принадлежности: Установка для определения момента инерции махового колеса и силы трения в упоре, секундомер, линейка, маятник Максвелла.
КРАТКАЯ ТЕОРИЯ
1. Определение момента инерции махового колеса и силы трения в упоре.
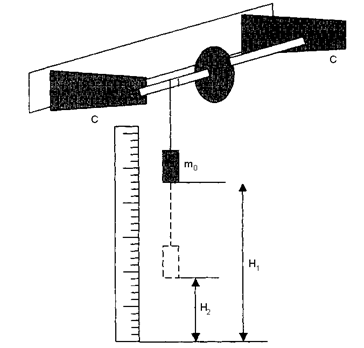
Прибор состоит из махового колеса, насаженного на вал и отсчетной линейки (см. рис. 1). Вал установлен на шарикоподшипниках С. На него наматывается шнурок, к концу которого крепится чашка массой m0.
Если считать массу чашки вместе с грузом m, то в результате движения до полного разматывания шнурка груз проходит расстояние h1;это означает, что в начальный момент движения система обладала запасом потенциальной энергии
.
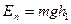Потенциальная энергия расходуется на преодоление силы трения и увеличение кинетической энергии системы, т.е. закон сохранения энергии имеет вид:
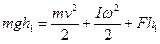, (1)
где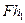 
- работа по преодолению силы трения.
Уравнение (1) относится к тому моменту времени, когда груз находится в наиболее низком положении. Силу трения можно определить, исходя из следующих соображений. Вращаясь по инерции, маховое колесо поднимает груз на высоту h2<h1, при этом система будет обладать потенциальной энергией
.
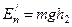Убыль потенциальной энергии равна работе по преодолению силы трения:
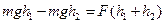. (2)
Отсюда
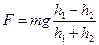. (3)
Для определения момента инерции I заменим в уравнении (1) ω и v. Так как движение равноускоренное без начальной скорости, то
,
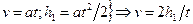где t - время опускания груза.
Угловая скорость равна
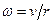, (4)
где r - радиус вала, в результате
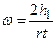. (5)
Подставляя выражения (3), (4) и (5) в (1), после соответствующих преобразований получим, что
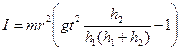. (6)
Ход работы
1. Определяют по шкале высоту h1.
2. Наматывают шнурок на ось и, опуская груз, определяют время t прохождения грузом пути.
3. Одновременно находят высоту поднятия груза до наивысшей точки h2.
4. Измерения повторяют по 3 раз для различных начальных высот h1, данные заносят в табл. 1 и рассчитывают момент инерции I и силу трения F.
5. Определяют погрешности.
Таблица 1. Определение момента инерции махового колеса
И силы трения в упоре
| № опыта | Данные наблюдений | Результаты расчетов | |||||||
| h1, м | h2, м | t, c | I, кг·м2 | Δ I, кг·м2 | ε I, % | F, Н | Δ F, Н | εF, % | |
| Ср. знач. | |||||||||
| Ср.знач. |
II. Определение момента инерции свободного маятника Максвелла и момента инерции кольца.
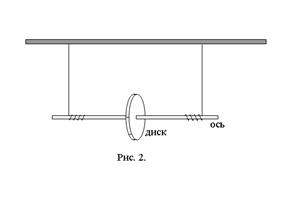
При вращательном движении маятника Максвелла (рис. 2), на основании закона сохранения энергии (пренебрегая силой трения), можно связать между собой три величины: момент силы натяжения нити M, угловое ускорение ε и момент инерции маятника I.
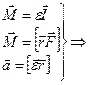
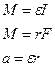, так как 
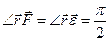, (7)
где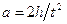 
- линейное ускорение движения; h - длина маятника, равная высоте, на которую он поднимается; т - масса оси маятника вместе с диском, равная 
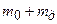, где m0 – масса оси, mд – масса диска; t - время падения маятника; g - земное ускорение свободного падения.
Исходя из представленного можно записать:
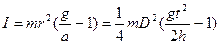. (8)
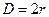- внешний диаметр оси маятника вместе с намотанной на нее нитью подвески.
Ход работы
1. Проводят вначале опыт с одним свободным маятником, по формуле
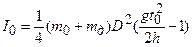(9)
находят момент инерции I0 свободного маятника. D – диаметр оси маятника вместе с намотанной нитью (D=10,8 мм).
2. Проделывают опыт с наложенным кольцом, находят момент инерции I всей системы
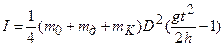, (10)
тK - масса кольца.
Момент инерции кольца определяют по формуле
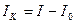. (11)
3. Вычисляют теоретический момент инерции кольца IKT
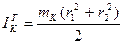, (12)
где r1 и r2 - внутренний и внешний радиусы кольца (измеряются штангенциркулем).
4. Результаты заносят в табл. 2.
тK=0,387 кг, то=0,033 кг, тд=0,1245 кг
Таблица 2. Определение момента инерции свободного маятника Максвелла
и момента инерции кольца
| № опыта | Данные наблюдений | Результаты расчетов | |||||||
| h, м | t0, c | t, c | I0, кг·м2 | I, кг·м2 | IK, кг·м2 | Δ IK, кг·м2 | ε, % | IКТ, кг·м2 | |
| 1. 2. 3. | |||||||||
| Среднее значение |
Контрольные вопросы
- Дайте определение понятий: момент инерции, момент силы, момент импульса.
- Используя формулу для кинетической энергии поступательного движения, получите выражение для кинетической энергии вращательного движения.
- Чему равна кинетическая энергия при плоском движении?
- Выведите формулу для момента инерции диска и толстостенного цилиндра.
Литература
1. Кортнев А.В. Практикум по физике. М., 1963.
2. Иверонова В.И. Физический практикум. М., 1953.
3. Стрелков С.П. Механика. М., 1952.
4. Матвеев А.Н. Механика. М., 1983.
5. Сивухин Д.В. Общий курс физики. Механика. М., 1983.
| 
|
| Рис. 1 |