ДОМАШНЕЕ ЗАДАНИЕ №5
ПО КУРСУ______________________________________________________________________
ТЕМА__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
ПРЕПОДАВАТЕЛЬ___________________________
СТУДЕНТ___________________________________
Выкса 2017
Содержание:
Задача. 3
Отделение корней. 4
Уточнение корней методом половинного деления. 5
Уточнение корней методом Ньютона. 6
Уточнение корней методом итераций. 8
Задача
Решить нелинейное уравнение
cos(2/x)-2*sin(1/x)+1/x=0
на интервале [1;2] с точность е=0,001 и шагом 0,2
Данную задачу можно решить несколькими способами:
1. Метод половинного деления
2. Метод Ньютона
3. Метод итераций
Решение задачи состоит из двух главных действий:
· отделение корней
· уточнение корней
Отделение корней
Выполним отделение корней на заданном участке. Для этого воспользуемся шаговым методом отделения корней, когда на определенном шаге вычисляется значение функции и определяется ее знак. Если при переходе с одного частичного интервала на другой происходит смена знака, то на выделенном интервале существует корень. Найдем значения функции в точках: 1; 1,2; 1,4; 1,6; 1,8; 2.
| x | f(x) |
| -1,099 | |
| 1,2 | -0,743 |
| 1,4 | -0,454 |
| 1,6 | -0,230 |
| 1,8 | -0,056 |
| 0,081 |
| x | f(x) |
| =B2 | =COS(2/C8)-2*SIN(1/C8)+1/C8 |
| =C8+$B$5 | =COS(2/C9)-2*SIN(1/C9)+1/C9 |
| =C9+$B$5 | =COS(2/C10)-2*SIN(1/C10)+1/C10 |
| =C10+$B$5 | =COS(2/C11)-2*SIN(1/C11)+1/C11 |
| =C11+$B$5 | =COS(2/C12)-2*SIN(1/C12)+1/C12 |
| =C12+$B$5 | =COS(2/C13)-2*SIN(1/C13)+1/C13 |
Из анализа полученных значений следует, что функция меняет знак на интервале [1,8;2], следовательно, этот частичный интервал является интервалом изоляции корня, т.е. на этом интервале существует корень.
Уточнение корней методом половинного деления
Определим новое приближение корня в середине выделенного интервала [1,8;2]

Найдем значение функции в точке x

Определим знак на левом интервале [a;x]:

Знак интервала отрицательный, следовательно, корень находится в левой части выделенного интервала [1,8;2], т. е. на интервале [1,8;1,9]. Примем b=1,9
Выполним проверку:

Условие не выполняется. Повторяем процесс вычисления.
| a | 1,800 | 1,800 | 1,850 |
| b | 2,000 | 1,900 | 1,900 |
| x | 1,900 | 1,850 | 1,875 |
| f(x) | 0,017 | -0,018 | 0,000 |
| f(a) | -0,056 | -0,056 | -0,018 |
| далее | далее | верно |
| a | =C12 | =ЕСЛИ(B25*B26<0;B22;B24) | =ЕСЛИ(C25*C26<0;C22;C24) |
| b | =C13 | =ЕСЛИ(B26*B25<0;B24;B23) | =ЕСЛИ(C26*C25<0;C24;C23) |
| x | =(B23+B22)/2 | =(C23+C22)/2 | =(D23+D22)/2 |
| f(x) | =COS(2/B24)-2*SIN(1/B24)+1/B24 | =COS(2/C24)-2*SIN(1/C24)+1/C24 | =COS(2/D24)-2*SIN(1/D24)+1/D24 |
| f(a) | =COS(2/B22)-2*SIN(1/B22)+1/B22 | =COS(2/C22)-2*SIN(1/C22)+1/C22 | =COS(2/D22)-2*SIN(1/D22)+1/D22 |
| =ЕСЛИ(ABS(B25)<$E$1; "верно";"далее") | =ЕСЛИ(ABS(C25)<$E$1; "верно";"далее") | =ЕСЛИ(ABS(D25)<$E$1; "верно";"далее") |
Условие выполняется при x=1,875, следовательно, это и будет корень уравнения
Уточнение корней методом Ньютона
Идея метода состоит в замене исходной функции ее линейной моделью в окрестностях начального значения корня x0 в виде касательной. Такая замена позволяет приближенно вычислить исходную функцию F(x0) по линейной функции

Отсюда, решение уравнения описывается итерационной формулой
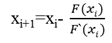
Итерационный процесс начинают с того конца отрезка на котором выполняется условие сходимости:

По условию задачи требуется найти приближенно корень уравнения на частичном интервале [1,8;2]. За начальное приближение принимается тот из концов отрезка, на котором выполняется условие сходимости.
Проверим выполнение условия сходимости в точке а=1,8. Для этого найдем вторую производную от нашей функции.
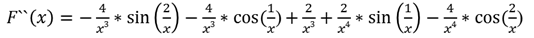

Условие выполняется. За нулевое приближение примем значение x=1.8. Вычислим первую производную:

Вычислим первое приближение к корню уравнения:

Погрешность вычисления:
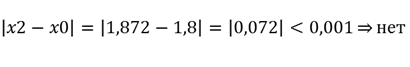
Условие не выполняется. Выполняем повторные приближения.
| x0 | 1,800 | 1,872 | 1,876 |
| x | 1,872 | 1,876 | 1,876 |
| f(x0) | -0,056 | -0,002 | 0,000 |
| f(x0)` | 0,769 | 0,706 | 0,703 |
| далее | далее | верно |
| x0 | =B22 | =B32 | =C32 |
| x | =B31-(B33/B34) | =C31-(C33/C34) | =D31-(D33/D34) |
| f(x0) | =COS(2/B31)-2*SIN(1/B31)+1/B31 | =COS(2/C31)-2*SIN(1/C31)+1/C31 | =COS(2/D31)-2*SIN(1/D31)+1/D31 |
| f(x0)` | =(2/B31^2)*SIN(2/B31)+ (2/B31^2)*COS(1/B31)-1/B31^2 | =(2/C31^2)*SIN(2/C31)+ (2/C31^2)*COS(1/C31)-1/C31^2 | =(2/D31^2)*SIN(2/D31)+ (2/D31^2)*COS(1/D31)-1/D31^2 |
| =ЕСЛИ(ABS(B31-B32)<$E$1; "верно";"далее") | =ЕСЛИ(ABS(C31-C32)<$E$1; "верно";"далее") | =ЕСЛИ(ABS(D31-D32)<$E$1;"верно";"далее") |
Условие выполняется при x=1,876.