Рассмотрим положительный числовой ряд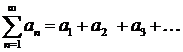 
(4.1). Теорема 4.9. Если существует предел корня 
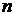-ой степени из общего члена ряда (4.1): 
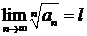. Тогда при l > 1 ряд (4.1) расходится, а при l < 1 сходится.
При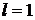 
радикальный признак Коши не дает ответа о сходимости ряда. В этом случае н ужно использовать другой признак.
Р адикальный пр изнак Коши является более сильным признаком, чем признак Даламбера. Иногда он может дать ответ на вопрос о сходимости ряда, когда признак Даламбера не даёт ответа на этот вопрос. Но если признак Коши не даёт ответа на вопрос о сходимости ряда, то и признак Даламбера тоже не даёт ответа на этот вопрос.
Радикальный признак Коши обычно использует в тех случаях, когда общий член ряда содержит степени чисел или многочленов, либо когда корень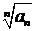 
хорошо извлекается.
Пример 4. Исследовать сходимость ряда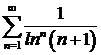 
.
Решение. Общий член ряда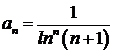 
содержит 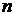-ую степень
Находим предел: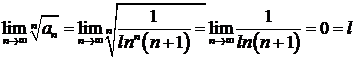 
Так как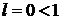 
, то заданный ряд сходится
Знакопеременные ряды
Определение 4.6. Числовой ряд 
(4.2)
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Определение 4.7. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.
Теорема 4.10. Всякий абсолютно сходящийся ряд является сходящимся. Или пусть имеется знакопеременный ряд (4.2). Если сходится ряд, составленный из модулей членов данного ряда: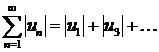 
, то сходится и сам знакопеременный ряд (4.2).
Если ряд абсолютно сходится, то ряд, полученный после любой перестановки его членов, тоже абсолютно сходится и имеет ту же самую сумму, что и исходный ряд.
Пример. Исследовать на сходимость ряд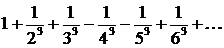 
.
Данный ряд является знакопеременный. Исследуем его на абсолютную сходимость. Ряд, составленный из модулей членов исходного ряда:
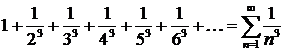представляет собой обобщенно-гармонический ряд с показателем 
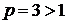, который сходится. Следовательно, по теореме 4.10, и заданный знакопеременный ряд является сходящимся.
Определение 4.7. Если знакопеременный ряд (4.2) сходится, а ряд, составленный из абсолютных величин его членов, расходится, то данный ряд называется условно сходящимся .
Знакочередующиеся ряды
Определение 4.8. Числовой ряд называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки:
(4.3)
где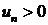 
для всех натуральных .
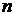Примерами знакочередующихся числовых рядов могут служить следующие ряды:
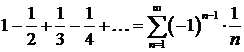и 
.
Знакочередующиеся ряды исследуют вначале на абсолютную сходимость, как знакопеременные ряды. Если знакочередующийся ряд абсолютно сходится, то, по теореме 4.10, исходный знакочередующийся ряд является сходящимся. Если знакочередующийся ряд абсолютно расходится, то исходный ряд исследуют на условную сходимость.
Имеет место достаточный признак сходимости (условной) знакочередующихся рядов.
Признак Лейбница.
Теорема 4.11.
Знакочередующийся ряд (4.3)
(где 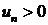для всех натуральных 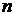), сходится, если выполняются два условия:
1) последовательность абсолютных величин членов ряда(4.3) монотонно убывает, т.е.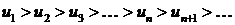 
;
2) абсолютная величина общего члена ряда (4.3) стремится к нулю: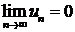 
.
При этом сумма S ряда удовлетворяет неравенству: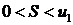 
.
Определение 4.9. Ряды, для которых выполняются условия теоремы Лейбница, называются рядами Лейбница.
Замечание:
Исследование знакочередующегося ряда
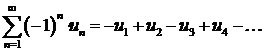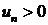( для всех натуральных ),
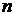с отрицательным первым членом сводится к исследованию ряда (4.3) после умножения всех его членов на (-1).
Пример
Исследовать на сходимость знакочередующийся ряд:
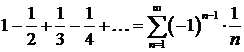
Решение.
Вначале исследуем на абсолютную сходимость. Ряд 
, составленный из абсолютных величин данного ряда, является гармоническим рядом, который расходится. Вывод: заданный ряд абсолютно расходится.
Исследуем заданный ряд на условную сходимость. Проверяем условия теоремы Лейбница.
Члены данного ряда по абсолютной величине монотонно убывают:
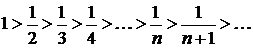и абсолютная величина общего члена ряда стремится к нулю: 
.
Следовательно, по признаку Лейбница заданный ряд сходится. Эта сходимость – условная.Ответ: данный ряд сходится условно.