Спектральное представление периодических сигналов.

Частотный анализ детерминированных сигналов.

Математический аппарат спектрального анализа.

Для частотного представления сигналов было выбрано преобразование Фурье, т. е. разложение по синусам и косинусам (а не по форме, к примеру прямоугольной) т. к. синус и косинус собственные функции линейного фильтра, т. е. эти функции не изменяют своей формы при прохождении через линейный фильтр.

Такое преобразование, впервые было применено Бернулли и Эйлером и рассматривалось лишь как метод решения задач математической физики. И только начиная с 20-х годов, вследствие бурного развития отраслей техники, связанных с колебаниями различного рода, спектральное представление получило всеобщее признание.

Известно, что любая функция, удовлетворяющая условиям Дирихле (она ограничена, кусочно-непрерывная и имеет на протяжении периода конечное число экстремумов), может быть представлена в виде бесконечной, в общем случае, суммы гармонических составляющих – рядом Фурье. Известны две наиболее часто применяемые формы разложения в ряд Фурье периодического колебания – тригонометрическая и комплексная.

Повторим и продолжим.

Тригонометрическая форма имеет следующий вид:

(1)

где:

- постоянная составляющая;

и 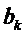-коэффициенты ряда Фурье;

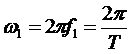- частота основной (первой) гармоники;

- частота к- й гармонической составляющей.

В эту сумму входят как четные, так и нечетные гармоники с амплитудами ак и bк, которые вычисляются по следующим формулам (2):

Тригонометрический ряд Фурье можно записать в более компактной форме, перейдя от переменных ак и bк к переменным Ак и φк в соответствии с формулами (3):

Эта замена соответствует переходу от декартовых к полярным координатам. Выполнив на основе (3) элементарные преобразования, получим следующую эквивалентную (1) тригонометрическую форму ряда Фурье:

(4)

Из (4) видно, что Ак представляет собой амплитуду, а φк - начальную фазу к-й гармоники.

Амплитуды Ак и начальные фазы φк принимают конкретные значения в зависимости от формы сигнала.

Комплексная форма ряда Фурье представляется в виде:

где: .

Спектральное представление периодических сигналов.

Графики, соответствующие тригонометрической форме (4) спектрального разложения функции x(t) представлены на рисунке 1:

Диаграммы распределения по частоте амплитуд и фаз гармонических составляющих называются спектральными диаграммами сигнала.

Линии, соответствующие амплитудам и фазам гармоник называются спектральными линиями.

Закон распределения амплитуд гармоник, составляющих периодический сигнал по частоте, называется спектром амплитуд, а закон распределения фаз – спектром фаз.

Если же нас не интересуют значения амплитуд и начальных фаз гармоник, входящих в состав сложного колебания, а интересуют только частоты, то говорят о спектре частот сигнала.

Особенности спектра периодического сигнала:

 

1) спектр линейчатый (дискретный), так как он состоит из отдельных равноотстоящих друг от друга спектральных линий, соответствующих дискретным частотам 0, w1, 2w1, 3w1, 4w1 и т. д.

2) описывается рядом Фурье, тригонометрической формой ряда Фурье, комплексной формой ряда Фурье.

 

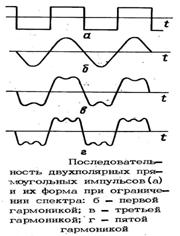
Рассмотрим, как изменяется спектр амплитуд при изменении длительности импульса, но при постоянном периоде последовательности импульсов (рис. 2).

Спектральные диаграммы обладают "лепестковой" структурой.

При τи – var, а Т – const изменяется ширина "лепестков" спектральной диаграммы и соотношения между амплитудами гармонических составляющих спектра, а расстояние между соседними спектральными линиями остаются постоянными.

При увеличении τи "лепесток" становится уже, удельный вес постоянной составляющей и гармоник с небольшими порядковыми номерами возрастает, а высших – уменьшается.

Если, наоборот, τи уменьшается, то "лепесток" расширяется, удельный вес гармоник с небольшими порядковыми номерами уменьшается, а удельный вес высших гармоник растет.

 

Рассмотрим распределение мощности в спектре периодического колебания.

 

Предположим, что исходный сигнал представляет собой ток i (t) – протекающий по сопротивлению r и описываемый сложной периодической функцией времени с периодом изменения Т.

 

 

		r

 

- средняя мощность, выделяемая на резисторе r.

 

- квадрат действующего значения тока.

 

 

Представив ток i (t) рядом Фурье, получим следующее выражение для, :

 

 

()

 

 

Следовательно:

 

 

 

где:

 

Таким образом, средняя мощность, выделяемая сложным периодическим сигналом (током) в резисторе, равна сумме средних мощностей, выделяемых на этом резисторе отдельными гармониками тока и его постоянной составляющей. По виду огибающей можно судить о распределении мощности в спектре периодического колебания и выбирать полосу пропускания цепи (практическую ширину спектра), обеспечивающую достаточно полное использование мощности сигнала.

Ширину спектра ∆F определяют как разность наибольшей и наименьшей частот полосы, в пределах которой амплитуды гармоник превышают некоторым образом определенную минимальную амплитуду: ∆F = f2 –f1.