Дифференциальный оператор Гамильтона
Дифференциальный оператор Гамильтона (оператор Ѵ̅) применяют для сокращения записи различных операций над скалярными и векторными величинами.
Под дифференциальным оператором Гамильтона (оператором набла) понимают сумму частных производных по трем координатным осям, умноженные на соответствующий единичный вектор (орты). В декартовой системе координат его записывают так:
Ѵ̅= ī*  j̅*
j̅* 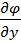 + k̅*
+ k̅* 
Ѵ̅- может быть применен как к скалярным так и к векторным функциям. Применим оператор Ѵ̅ к потенциалу ϕ.
Ѵ̅ϕ= (i̅* 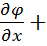 j̅*
j̅* 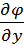 + k̅*
+ k̅*  )ϕ= i̅*
)ϕ= i̅* 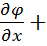 j̅*
j̅* 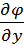 + k̅*
+ k̅* 
Сравнивая полученное выражение с выражением для градиента потенциала (2) получим:
gradϕ= Ѵ̅ϕ т.е. эти выражения тождественны.
Замечание. Выражение градиента потенциала в других системах координат можно найти в учебной и справочной литературе.
Свободные и связанные заряды. Поляризация вещества.
Заряды, которые под воздействием силы поля могут свободно перемещаться в веществе, причем перемещение их не ограничивается внутри полярными силами- называются свободными зарядами.
Электрические заряды, входящие в состав вещества и удерживаемые в определенных положениях внутримолекулярными силами – называются связанными зарядами. Сумма положительных зарядов равна сумме отрицательных связанных зарядов.
Если какое-либо диэлектрическое тело поместить в электрическое поле, то в нем происходит упорядоченное изменение расположения связанных зарядов, называемое поляризацией.
Это изменение расположения проявляется в том, что отрицательные связанные заряды в теле перемещаются в направлении более высокого потенциала, а положительные связанные заряды в сторону более низкого потенциала. Заряды сместятся настолько, что силы взаимодействия электрического поля на связанные заряды уравновешиваются молекулярными силами. В результате поляризации на поверхности вещества как бы обозначаются связанные заряды.
В поляризованном веществе молекулы в электрическом отношении представляют собой диполи(т.е. два связанных между собой и равных по величине заряда +q и –q) Если принял длину диполя равной L, то произведение ql̅ называют электрическим моментом диполя.
Под действием внешнего электрического поля диполи стремятся ориентироваться в пространстве таким образом, чтобы электрический момент их был направлен параллельно вектору напряженности электрического поля.
Электрический момент суммы диполей, находящихся в объёме вещества V, отнесенный к объёму V, при стремлении V к нулю- называется вектором поляризации(поляризованностью) и обозначается P̅.
P̅ = 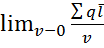
Для однородных и изотропных диэлектриков P̅ пропорционален напряженности электрического поля Е̅.
P̅= ɛ0*x*E̅= xа*E̅
Где x- относительная диэлектрическая восприимчивость
Xа = ɛ0*x – абсолютная диэлектрическая восприимчивость, характеризующая способность данного диэлектрика и поляризации.
ɛ0= 8, 86* 10-12 [ Ф/м]- электрическая постоянная
Диэлектрики в зависимости от происходящих в них процессах при поляризации делятся на 2 группы.
1-я группа. К ней относится диэлектрики, молекулы которых при отсутствии внешнего электрического поля электрически нейтральны, т.е. в них центры действия положительных и отрицательных зарядов совпадают (к ним относятся: азот, парафин, водород и др.)
2-я группа. К ней относится диэлектрики, молекулы которых при отсутствии внешнего электрического поля представляют собой диполи, т.е. центры действия положительных и отрицательных зарядов этих молекул при отсутствии внешнего электрического поля не совпадают- к таким диэлектрикам относится, например, хлористый водород. Поляризация в этой группе состоит в том, что полярные молекулы стремятся повернуться таким образом, чтобы их электрический момент был направлен по внешнему электрическому полю.