Порядок выполнения работы

1. Решить задачу:

- составной резистор образуется из десяти последовательно соединенных резисторов трех номиналов (R1, R2, R3). Количество резисторов каждого номинала и их номинальные значения принимаются в соответствии с вариантом, выданным преподавателем. Определить доверительные границы погрешности составного резистора для указанной в таблице вероятности .

2. Для решения этой задачи необходимо:

2.1 Для каждого массива аргументов j определить оценки математического ожидания и среднего квадратического отклонения как

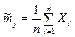и .

2.2 Определить оценку с.к.о. оценки математического ожидания как

.

2.3 Найти номинальное значение составного резистора как

.

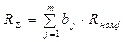2.4 Определить доверительную границу систематической составляющей погрешности для каждого аргумента как

.

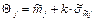2.5 Определить доверительные границы систематической составляющей погрешности

,

где - число резисторов данного номинала в составном резисторе, а - общее число номиналов.

2.6 Вычислить дисперсию случайной погрешности результата как

и соответствующее ей значение с.к.о. .

2.7 Определить доверительные границы для случайной составляющей погрешности как

.

2.8 Найти границы общей погрешности как

.

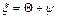2.9 Значение составного резистора с доверительной вероятностью

записать как

, , .

 

РАБОТА №5

«ИСПОЛЬЗОВАНИЕ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ ПРИ ОБРАБОТКЕ РЕЗУЛЬТАТОВ СОВМЕСТНЫХ

ИЗМЕРЕНИЙ»

Цель работы - ознакомиться с методиками, применяемыми при обработке результатов совместных измерений по методу наименьших квадратов.

Основные положения

Совместные измерения — одновременные измерения нескольких разноименных величин для нахождения зависимости между ними. Уравнение совместного измерения можно представить как

(7)

где x, y, z, q - измеряемые величины; A,B,C - величины которые необходимо определить. Наибольшее распространение при обработке совместных измерений нашел метод наименьших квадратов (МНК) [7]. Суть его состоит в следующем:

При проведении n измерений величин x, y, z, … и подстановке их в уравнение (7) получается система из n уравнений:

,

(8)

в которых точное равенство невозможно из-за того, что измеряемые величины входят в каждое из уравнений (7) с погрешностями. Если 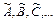- наилучшие приближения к истинным значениям неизвестных A, B, C, ….. Поскольку эти оценки определены со своими погрешностями, то каждое из уравнений (8) будет обращаться в тождество, если к правой части добавить некоторое слагаемое ν_i, называемое остаточной погрешностью условных уравнений:

(9)

В системе n условных уравнений (9) - оценки величин A, B, С.., которые будут определены ниже в результате предложенного метода обработки результатов измерений. Особенность системы (9) состоит в том, что невозможно подобрать для всех уравнений значения ν_i такие, чтобы выполнялись все уравнения одновременно. Поэтому рассматривают методы одновременной минимизации остаточных погрешностей.

В соответствии в МНК оценки 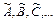выбирают таким образом, чтобы обеспечить минимум суммы квадратов остаточных погрешностей условных уравнений, т.е. минимизировать величину:

(10)

Минимум V будет иметь место при равенстве нулю всех частных производных искомых величин одновременно, т.е. при

.

(11)

Полученная система из m нормальных уравнений позволяет определить наилучшие оценки искомых величин. Дисперсия условных уравнений будет равна:

.

(12)

А СКО результаты измерений искомых величин при этом могут быть определены из формул:

и т.д.

(13)

где Δ - определитель (детерминант) системы (11); A₁₁, A₂₂, A₃₃, …A_mm -алгебраическое дополнение элементов детерминанта , - минор определителя, полученный вычеркиванием i -ой строки и k -го столбца.

При обосновании МНК в математической статистике предполагается, что результаты измерений удовлетворяют следующим условиям:

- значения аргументов известны точно;

- результаты измерений содержат лишь случайные погрешности, которые независимы, имеют нулевые средние значения и одинаковые дисперсии;

-погрешности измеряемых величин имеют нормальное распределение.

Доверительные интервалы для истинных значений измеряемых величин строят на основе распределения Стьюдента при числе степеней свободы, равном n-m, или на основе нормального распределения, если результаты измерений можно считать нормальными.

Для случая равноточных измерений y и x, связанных линейным уравнением

у = a + bx.

(14)

Искомыми величинами являются a и b. Равноточность предполагает, что для всех результатов измерений i значений y_i и x_i их дисперсии не зависят от величин y и x. Кроме того, предполагается, что значение x_i задается в серии измерений точно, а учитывается только погрешность определения y_i, в состав которой входит погрешность, связанная с заданием величин x_i.

Подставив в (14) измеренные значения, можно получить систему уравнений:

,

,

.

Для получения условных уравнений в виде (9) к каждому из уравнений (8) добавляются (или вычитаются - это все равно) остаточные погрешности ν_i. После этого составляется соотношение типа (10)

Для отыскания минимума функции V определяются частные производные по искомым неизвестным а и b:

,

.

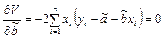После упрощения получается система нормальных уравнений

,

.

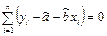Приведем эти уравнения к виду, удобному для решения

;

(15)

Решая (15) относительно неизвестных и , получим

;

.

Умножая числитель и знаменатель на и вводя обозначения , , , , , получаем

, .

(16)

В формулах (16) дисперсия характеризует рассеянность точно задаваемых значений x_i около среднего значения x на оси x. Если прямая (14) проходит через начало координат (), то формулы (16) значительно упрощаются:

, , .

Случайные погрешности оценок неизвестных a и b, если использовать соотношения (12), (13) и систему уравнений (15) будут равны

, ,

(17)

где - детерминант системы (15).

В данном случае СКО условных уравнений является СКО распределения y(x), и для нормального закона распределения y(x) на основании (13) может быть представлено в виде:

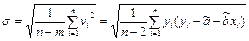
Параметры a и b выражаются через суммы всех случайных значений величин y(x). Поэтому закон их распределения, получающийся в результате свертки законов распределения y(x), нормальный независимо от вида закона распределения y(x).

Задание

Пусть зависимость электрического сопротивления композиционного материала от температуры выражается формулой R = R₀(1+ βt²). Для определения коэффициента β было проведено n равноточных измерений сопротивлений при различной температуре. Используя МНК, вычислить оценку коэффициента β с доверительной вероятностью P.