ЗАКОНЫРАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
1. Равномерное распределение.
2. Показательное распределение.
3. Нормальное распределение.
Вопрос 1. Равномерное распределение
При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями НСВ.
Плотности распределений НСВ называются так же законами распределений.
О.1.1. НСВ Х имеет равномерное распределение, если ее плотность распределения задается в виде:
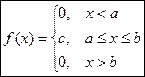 , (1)
, (1)
где с – некоторая постоянная.
Примеры равномерно распределенных НСВ:
1. Х – время ожидания на стоянке автобуса (СВ равномерно распределена на отрезке [0; l], где l – интервал движения между автобусами).
2. Х – ошибка при взвешивании случайно выбранного предмета, получающаяся от округления результата взвешивания до ближайшего целого числа (СВ Х имеет равномерное распределение на отрезке [-0,5; 0,5], где за единицу принята цена деления шкалы).
Найдем постоянную с в формуле (1).
По свойству функции f(x):
 Û
Û  Û
Û 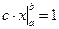 Û
Û  Þ
Þ 
Таким образом, плотность распределения для равномерно распределенной НСВ Х имеет вид:


Функция распределения для равномерно распределенной НСВ Х имеет вид:

График плотности распределения равномерно распределенной НСВ Х имеет вид:





f(x)


 0 a b x
0 a b x
График функции распределения равномерно распределенной НСВ Х имеет вид:
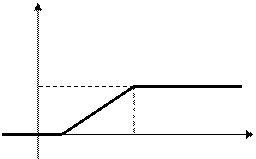 F(x)
F(x)
0 a b x
Математическое ожидание: 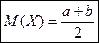
Дисперсия: 
Вероятность попадания СВ Х в интервал (х1; х2): 
Здесь предполагается, что (x1; x2) Ì [a; b]
Пример 1. Цена деления шкалы амперметра равна 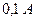 . Показания округляются до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая
. Показания округляются до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая  .
.
Решение
 Ошибку округления отсчета будем рассматривать как случайную величину
Ошибку округления отсчета будем рассматривать как случайную величину 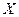 , которая распределена равномерно в интервале между двумя соседними целыми делениями.
, которая распределена равномерно в интервале между двумя соседними целыми делениями.
Дифференциальная функция имеет вид  .
.
В результате получим 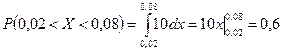 .
.
Вопрос 2. Показательное распределение
При решении ряда прикладных задач физики, биологии, астрономии, радиотехники, теории информации, теории надежности и т.п. приходится сталкиваться с обширным классом НСВ, распределение которых достаточно хорошо описывается экспоненциальным (показательным) законом.
О.2.1. НСВ Х имеет показательное (экспоненциальное) распределение, если ее плотность распределения задается в виде:
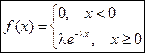 ,
,
где l > 0 – постоянная величина (параметр).
 График плотности распределения f(x) для показательно распределенной НСВ Х имеет вид:
График плотности распределения f(x) для показательно распределенной НСВ Х имеет вид:
f(x)
 l
l
0 
 x
x
Примеры показательно распределенных НСВ:
1. длительность телефонного разговора;
2. срок безотказной работы прибора;
3. время уничтожения цели одиночными выстрелами;
4. время обслуживания заявки в системе массового обслуживания.
Функция распределения для показательно распределенной НСВ Х имеет вид:




 F(x)
F(x)
0 x
Математическое ожидание: 
Дисперсия: 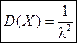
Вероятность попадания СВ Х в интервал (х1; х2): 
Вопрос 3. Нормальное распределение
О.3.1. НСВ Х имеет нормальное распределение, если ее плотность распределения задается в виде:
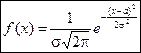 , (2)
, (2)
где а и s - параметры распределения.
Примеры нормально распределенных НСВ:
1) рост человека;
2) дальность полета снаряда;
3) ошибки измерений;
4) величина помехи на входе радиоприемного устройства в данный момент;
5) многие параметры радиодеталей (емкость, сопротивление, индукция)
Т.3.1. (вероятностный смысл параметров нормального распределения)
Математическое ожидание НСВ Х, распределенной по нормальному закону, равно параметру а этого закона, то есть:
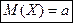 ,
,
а ее среднее квадратическое отклонение – параметру s, то есть:
 .
.
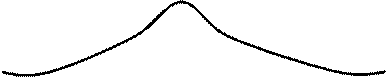
О.3.2. График плотности нормального распределения (1) называется нормальной кривой (кривой Гаусса).
 f(x)
f(x)



0 a x
Влияние параметров а и s на форму нормальной кривой можно описать следующим образом:
1. Изменение параметра а (математического ожидания) не изменяет форму кривой, а приводит лишь к ее сдвигу вдоль оси Ох (вправо, если а возрастает, и влево, если а убывает).
2. С возрастанием s максимальная ордината кривой убывает, а сама кривая становится более пологой, то есть сжимается к оси Ох; при убывании s кривая становится более «островершинной» и растягивается в положительном направлении оси Оу.
Вывод: параметр а (математическое ожидание) характеризует положение, а параметр s (среднее квадратическое отклонение) – форму нормальной кривой.