Показательные неравенства
Теоретическая часть.
1) Простейшие показательные неравенства имеют вид 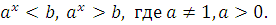
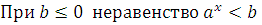 решений не имеет, а неравенство
решений не имеет, а неравенство 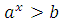 выполняется при всех значениях аргумента, поскольку
выполняется при всех значениях аргумента, поскольку 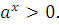
Используя свойство монотонности показательной функции делаем вывод, что неравенство 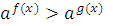 при
при 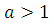 равносильно неравенству
равносильно неравенству 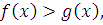 а при
а при 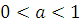 равносильно неравенству
равносильно неравенству 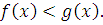
Методы решения произвольных показательных неравенств.
Решение большинства показательных неравенств сводится к решению простейших показательных неравенств.
А. Метод уравнивания оснований.
Примеры.
1) 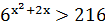 2)
2) 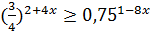
Решение
1)
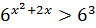
Т.к. y=6t – возрастающая, перейдем к равносильному неравенству:
x2+2x>3
x2+2x-3>0
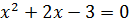
По теореме Виета:
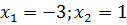
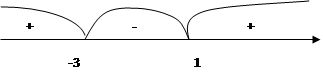 |
x
Ответ: 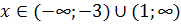
2)
|
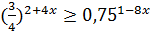
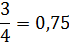








 -1/12 x
-1/12 x
Ответ: 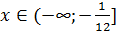
В. Метод решения, основанный на разложении на множители.
Примеры.
Пример 1. Решите неравенство: х 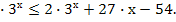
Решение.
О.О.: х 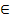 R
R
х 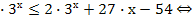 х
х 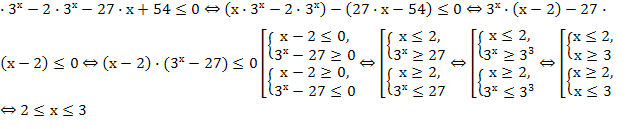
Ответ: 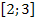 .
.
Пример 2. Решите неравенство: 3 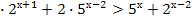 .
.
Решение.
3 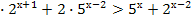
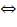 3
3 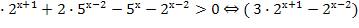 +(
+(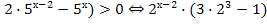 +
+ 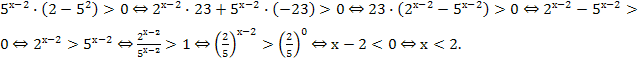
Ответ: 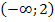 .
.
С. Метод введения вспомогательной переменной.
С помощью подстановки 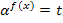 , где t
, где t 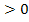 , неравенство приводится либо к квадратному неравенству относительно переменной t, либо к какому-нибудь другому неравенству относительно переменной t, решается относительно t, а затем ищется значение переменной х.
, неравенство приводится либо к квадратному неравенству относительно переменной t, либо к какому-нибудь другому неравенству относительно переменной t, решается относительно t, а затем ищется значение переменной х.
Примеры.
Пример 1. Решите неравенство: 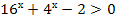 .
.
Решение.
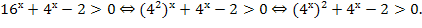 О.О.:
О.О.: 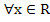
Пусть 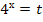 ,
, 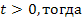
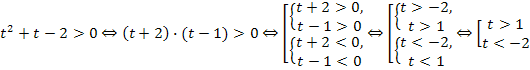
Вернемся к переменной х и получим два неравенства:
1) 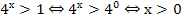 .
.
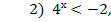 решений нет, так как
решений нет, так как 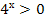 для
для 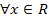 .
.
Ответ: 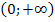 .
.
D. Неравенства, левая часть которых имеет вид А 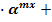 B
B 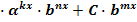 ,
,
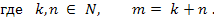
Неравенства такого типа решаются с помощью деления обеих частей на
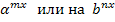 .
.
Примеры.
Пример 1. Решите неравенство: 3 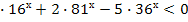 .
.
Решение.
3 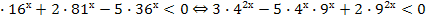 .
.
Разделим обе части последнего неравенства на 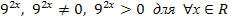 :
:
3 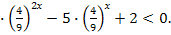 Введем новую переменную t =
Введем новую переменную t = 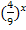 , t
, t 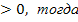
3 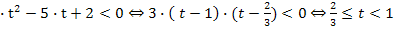 . Вернемся к переменной х:
. Вернемся к переменной х:
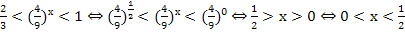 .
.
Ответ: 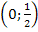 .
.
Е. Графический способ решения.
При решении неравенств графическим способом необходимо рассмотреть две функции, построить их графики в одной системе координат и выяснить при каких значениях аргумента значения одной функции больше (меньше) значений другой функции. Найденные значения аргумента и есть решения неравенства.
Примеры.
Пример 1. Решите неравенство: 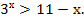
Решение.
Чтобы решить данное неравенство графическим способом, рассмотрим две функции: f(x)= 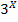 и g(x)= 11-х, D(f)=R, D(g)=R.
и g(x)= 11-х, D(f)=R, D(g)=R.
1.Функция f(x)= 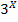 - показательная функция по основанию «3». Для построения графика зададим таблицу ее значений:
- показательная функция по основанию «3». Для построения графика зададим таблицу ее значений:
| х | -1 | ||||
f(x)= 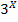
| 
|
2. Функция g(x)= 11-х - линейная функция, ее графиком является прямая.
| х | ||
| g(x)= 11-х |
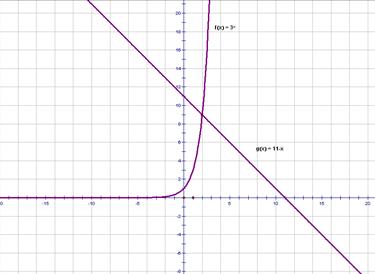
3. Построим графики этих функций в одной системе координат и выясним, при каких значениях переменной х выполнено неравенство: f(x) 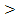 g(x).
g(x).
 | |||||
 | |||||
 | |||||
Рассмотрим два интервала: 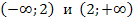 :
:
если х 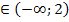 , то f(x)
, то f(x) 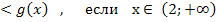 , f(x)
, f(x) 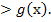 Значит, решением неравенства
Значит, решением неравенства 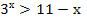 являются значения х, принадлежащие промежутку
являются значения х, принадлежащие промежутку 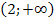 .
.
Ответ: 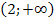 .
.
Пример 2. Решите неравенство: 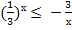 .
.
Решение.
Чтобы решить данное неравенство графическим способом, рассмотрим две функции: f(x) = 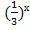 и g(x) =
и g(x) = 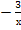 , D(f)=R, D(g)=
, D(f)=R, D(g)= 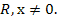
1.Функция f(x) = 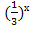 - показательная функция с основанием
- показательная функция с основанием  . Для построения графика зададим таблицу ее значений:
. Для построения графика зададим таблицу ее значений:
| х | -2 | -1 | |||
f(x)= 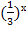
| 
| 
|
2. Функция g(x)= 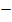
 – функция обратная пропорциональность, ее графиком является гипербола, расположенная во 2-й и 4-й координатных четвертях.
– функция обратная пропорциональность, ее графиком является гипербола, расположенная во 2-й и 4-й координатных четвертях.
| х | -6 | -3 | -1 | |||
g(x)= 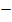 
| 0,5 | -3 | -1 | -0,5 |
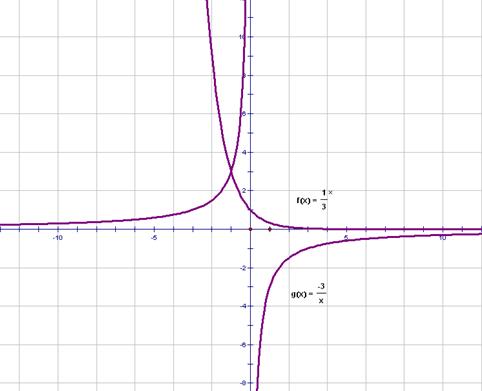
3. Построим графики этих функций в одной системе координат и выясним, при каких значениях переменной х выполнено неравенство: f(x) 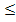 g(x).
g(x).
 | |||
 | |||
Рассмотрим три интервала: 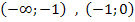 и
и 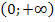 :
:
если х 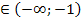 , то f(x)
, то f(x) 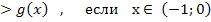 , то f(x)
, то f(x) 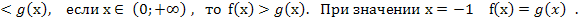 Значит, решением неравенства
Значит, решением неравенства 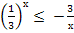 являются значения х, принадлежащие промежутку
являются значения х, принадлежащие промежутку 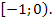
Ответ: 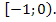
 -1/12
-1/12