Формулировка задачи: сколько кусков пиццы можно получить, делая n прямолинейных разрезов ножом? Или, каково максимальное число Ln областей, на которые плоскость делится n прямыми?

Эксперимент с тремя прямыми показывает, что добавленная третья прямая может рассекать самое большое три старых области вне зависимости от того, как расположены первые две прямые:
 Таким образом, L3=4+3=7 – самое большое, что можно сделать.
Таким образом, L3=4+3=7 – самое большое, что можно сделать.
Обобщая, приходим к следующему выводу: новая n-я прямая (при n>0) увеличивает число областей на k ó когда рассекает k старых областей ó когда пересекает прежние прямые в (k−1) различных местах. Две прямые могут пересекаться не более чем в одной точке. Поэтому новая прямая может пересекать (n−1) старых прямых не более чем в (n−1) различных точках, и мы должны иметь k ≤ n. Установлена верхняя граница:
Ln ≤ Ln-1+ n при n>0
В этой формуле можно достичь равенства следующим образом: проводим n-ю прямую так, чтобы она не была параллельна никакой другой прямой (следовательно, она пересекает каждую из них) и так, чтобы она не проходила ни через одну из имеющихся точек пересечения (следовательно, она пересекает каждую из прямых в различных местах). Поэтому рекуррентное соотношение имеет вид:
Ln = Ln-1+ n при n > 0
Теперь получим решение в замкнутой форме.
Ln = Ln-1+ n = Ln-2+ (n−1) + n = Ln-3+ (n−2) + (n−1) + n = … = L0+ 1 + 2+ +… + (n−2) + (n−1) + n = 1 + 
Ln =  + 1при n ≥ 0 (3)
+ 1при n ≥ 0 (3)
Докажем полученное равенство методом математической индукции.
1) База: n=0, L0=  = 1 (верно);
= 1 (верно);
2) Индуктивный переход: пусть доказано для всех чисел t ≤ (n–1). Докажем для t=n:
Ln = Ln-1+ n 
 =
=  =
= 
Из пунктов 1 и 2 следует: при n ≥ 0 Ln =  + 1
+ 1
 А теперь небольшая вариация на тему прямых на плоскости: предположим, что вместо прямых линий мы используем ломаные линии, каждая из которых представлена одним «зигом». Каково максимальное число Zn областей, на которые плоскость делится n такими ломаными линиями?
А теперь небольшая вариация на тему прямых на плоскости: предположим, что вместо прямых линий мы используем ломаные линии, каждая из которых представлена одним «зигом». Каково максимальное число Zn областей, на которые плоскость делится n такими ломаными линиями?


 Частные случаи:
Частные случаи:
 |  | ||||||
|
|
Ломаная линия подобна двум прямым с тем лишь отличием, что области сливаются, если «две» прямые не продолжать после их пересечения:
 Области 2, 3 и 4, которые были бы разделены при наличии двух прямых, превращаются в единую область в случае одной ломаной линии, т.е. мы теряем две области. И если привести все в надлежащий порядок, то точка излома должна лежать «по ту сторону» пересечений с другими линиями, и мы теряем только две области на одну линию. Таким образом,
Области 2, 3 и 4, которые были бы разделены при наличии двух прямых, превращаются в единую область в случае одной ломаной линии, т.е. мы теряем две области. И если привести все в надлежащий порядок, то точка излома должна лежать «по ту сторону» пересечений с другими линиями, и мы теряем только две области на одну линию. Таким образом,
Zn = L2n − 2n =  = 2n2 −n+1 при n ≥ 0 (4)
= 2n2 −n+1 при n ≥ 0 (4)
Сравнивая решения в замкнутой форме (3) и (4), мы приходим к выводу, что при большом n,
Ln ~  ,
,
Zn ~ 2n2 ,
так что ломаные линии дают примерно в четыре раза больше областей, чем прямые.
Задача Иосифа Флавия
Формулировка задачи: в круг выстроено n человек, пронумерованных числами от 1 до n, и исключается каждый второй из оставшихся до тех пор, пока не уцелеет только один человек. Определить номер уцелевшего, J(n).
 Например, при n = 10 порядок исключения – 2, 4, 6, 8, 10, 3, 7, 1, 9, так что остается номер 5, т.е. J(10) = 5. При n = 2 номер уцелевшего J(2) = 1. Можно было бы предположить, что J(n) =
Например, при n = 10 порядок исключения – 2, 4, 6, 8, 10, 3, 7, 1, 9, так что остается номер 5, т.е. J(10) = 5. При n = 2 номер уцелевшего J(2) = 1. Можно было бы предположить, что J(n) =  при четном n. Однако это не так – предположение нарушается при n = 4 и n = 6.
при четном n. Однако это не так – предположение нарушается при n = 4 и n = 6.
| N | ||||||
| J(n) |
J(n) всегда будет нечетно, т.к. первый обход по кругу исключает все четные номера. К тому же, если само n четно, мы приходим к ситуации, подобной той, с которой начали, за исключением того, что остается вдвое меньше людей, и их номера меняются.
Итак, решим поставленную задачу.
Допустим, что первоначально имеется 2n людей. После первого обхода мы остаемся с номерами:
 Следующий обход будет начинаться с номера 3. Это тоже самое, если бы мы начинали с n людей, за исключением того, что номер каждого уцелевшего удваивается и уменьшается на 1. Тем самым
Следующий обход будет начинаться с номера 3. Это тоже самое, если бы мы начинали с n людей, за исключением того, что номер каждого уцелевшего удваивается и уменьшается на 1. Тем самым
J(2n) = 2∙J(n) − 1 при n ≥ 1 (5)
Теперь можно быстро продвигаться к большим n. Например, нам известно, что J(10) = 5, поэтому J(20) = 2∙J(10) − 1 = 2∙5 − 1 = 9, аналогично J(40) = 2∙J(20) − 1 = 17, и вообще можно вывести, что
J(5∙2m) = 2m+1+1.
J(5∙2m) = J(2∙2m-1∙5) = 2∙J(2m-1∙5) − 1 = 2∙J(2∙2m-2∙5) − 1 = 22∙J(2m-2∙5)− 21 − 1 = =23∙J(2m-3∙5) − 22 − 21 − 1=24∙J(2m-4∙5) − 23 − 22 − 21 − 1= …= 2m∙J(5) − (2m-1+2m-2+ +…+23+22+21+1) = 2m∙J(5) −  = 2m∙3 − 2m + 1 = 2m+1+1.
= 2m∙3 − 2m + 1 = 2m+1+1.
Теперь посмотрим, что будет в случае, когда имеется 2n+1 людей. После первого обхода жертва с номером 1 уничтожается сразу после жертвы с номером 2n, и мы остаемся с номерами:
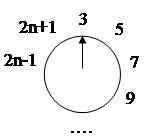 Получили почти первоначальную ситуацию с n людьми, но на этот раз номера уцелевших удваиваются и увеличиваются на 1. Таким образом,
Получили почти первоначальную ситуацию с n людьми, но на этот раз номера уцелевших удваиваются и увеличиваются на 1. Таким образом,
J(2n+1) = 2∙J(n) + 1 при n ≥ 1 (6)
Объединение уравнений (5) и (6) с уравнением J(1)=1 дает рекуррентное соотношение, которое определяет J во всех случаях:
J(1) = 1
J(2n) = 2∙J(n) − 1 при n ≥ 1 (7)
J(2n+1) = 2∙J(n) + 1 при n ≥ 1
Решим данное рекуррентное соотношение. Составим таблицу первых значений J(n):
| n | 2 3 | 4 5 6 7 | 8 9 10 11 12 13 14 15 | ||
| J(n) | 1 3 | 1 3 5 7 | 1 3 5 7 9 11 13 15 |
Если сгруппировать значения n по степеням двойки (в таблице эти группы отделены вертикальными линиями), то в каждой группе J(n) всегда будет начинаться с 1, а затем увеличиваться на 2. Итак, если записать n в виде n = 2m+k, где 2m – наибольшая степень 2, не превосходящая n, а k – то, что остается, то решение рекуррентного соотношения должно иметь вид:
J(2m+k) = 2k+1 при m ≥ 0 и 0 ≤ k < 2m (8)
(Если 2m ≤ n < 2m+1, то остаток k = n−2m удовлетворяет неравенству 2m≤k+2m<2m+1, т.е. 0 ≤ k < 2m)
Докажем (8) методом математической индукции по m.
1) База: m = 0 => k = 0
J(20+0) = J(1) = 2∙0 + 1 = 1 (верно);
2) Индуктивный переход: пусть верно для всех чисел t ≤ (m − 1). Докажем для t=m:
a) если m > 0 и 2m+k=2n, то k – четно и J(2m+k) = J(2(2m-1+  )) =
)) =  2∙J(2m-1+
2∙J(2m-1+  ) − 1
) − 1  2(2∙
2(2∙  + 1) −1 = 2k + 1
+ 1) −1 = 2k + 1
b) если m > 0 и 2m+k=2n+1, то k – нечетно (т.е. k=2t+1) и J(2m+k) = = J(2m+(2t+1)) = J(2(2m-1+t) +1)  2∙J(2m-1+ t) + 1
2∙J(2m-1+ t) + 1  2(2t+1) + 1 = 2k + 1
2(2t+1) + 1 = 2k + 1
Другой способ доказательства, когда k – нечетно:
Можно заметить, что J(2n+1) − J(2n) = 2, тогда J(2m+k) = 2 + J(2m + (k− −1)) 
 J(2m+k) = 2 + 2(k −1) + 1 => J(2m+k) = 2k+1.
J(2m+k) = 2 + 2(k −1) + 1 => J(2m+k) = 2k+1.
Из пунктов 1 и 2 следует: при m ≥ 0 и 0 ≤ k < 2m J(2m+k) = 2k+1.
Решение всякой задачи может быть обобщено так, что его можно применить к более широкому кругу задач. Поэтому изучим решение (8) и исследуем некоторые обобщения рекуррентного соотношения (7).
Обратимся к двоичным представлениям величин n и J(n) (т.к. степени 2 играли важную роль в нашем поиске решения).
n = (bm bm-1 … b1 b0)2;
т.е. n = bm2m + bm-12m-1 + … + b12 + b0
где каждое bi равно 0 или 1, причем старший бит bm равен 1. Вспоминая, что n=2m+k, последовательно получаем:
n = (1 bm-1 … b1 b0)2
k = (0 bm-1 … b1 b0)2
(т.к. k= n−2m = 2m + bm-12m-1 + … + b12 + b0 − 2m = 0∙2m + bm-12m-1 + …+ b12 + b0)
2k = (bm-1 … b1 b0 0)2
(т.к. 2 k=2(bm-12m-1 +bm-22m-2 …+ b12 + b0)=bm-12m + bm-22m-1 + … + b122 + b02+0)
2k+1 = (bm-1 … b1 b0 1)2
J(n) = (bm-1 … b1 b0 bm)2
(т.к. J(n) = 2k+1 и bm = 1)
Таким образом, мы получили, что
J((bm bm-1 … b1 b0)2) = (bm-1 … b1 b0 bm)2 (9)
т.е. J(n) получается путем циклического сдвига двоичного представления n влево на один сдвиг.
Рассмотрим свойства функции J(n).
Если мы начнем с n и итерируем J-функцию m+1 раз, то тем самым осуществляем циклический сдвиг на m+1 битов, а т.к. n является (m+1)-битовым числом, то мы могли бы рассчитывать в итоге снова получить n. Но это не совсем так. К примеру, если n = 27, то J(11011) = ((10111)2), но затем J(10111) = ((1111)2), и процесс обрывается: когда 0 становится старшим битом – он пропадает (т.к. принято, что коэффициент при старшей степени не равен 0). В действительности J(n) всегда должно быть ≤ n по определению, т.к. J(n) есть номер уцелевшего; и если J(n) < n, мы никогда не сможем получить снова n в следующих итерациях.
Многократное применение J порождает последовательность убывающих значений, достигающих, в конце концов «неподвижной точки» n, такой, что J(n)=n. Докажем, что J порождает последовательность убывающих значений, т.е. покажем, что 2n > 2n-1 + 2n-2 +…+21 + 1 при n ≥ 1.
Докажем методом математической индукции по n:
1) База: n=1, 21 > 20 (верно);
2) Индуктивный переход: пусть верно для всех чисел t ≤ (n–1), т.е. выполняется неравенство 2t-1 > 2t-2 + 2t-3 +…+21 + 1. Докажем для t=n:
(2n-1 > 2n-2 + 2n-3 +…+21 + 1) умножим на 2, получим 2n > 2n-1 + 2n-2 +…+22 + 21. Левая и правая части неравенства четные числа, тогда между ними есть хотя бы одно нечетное число, следовательно, прибавление 1 к правой части неравенства (четное число +1 = нечетное число) неравенство не изменит. Т.о. получаем нужное нам неравенство: 2n > 2n-1 + 2n-2 +…+21 + 1 при n ≥ 1.
 Свойство циклического сдвига позволяет выяснить, чем будет «неподвижная точка»: итерирование функции m и более раз всегда будет порождать набор из одних единиц со значением
Свойство циклического сдвига позволяет выяснить, чем будет «неподвижная точка»: итерирование функции m и более раз всегда будет порождать набор из одних единиц со значением  , где ν(n) – число равных 1 битов в двоичном представлении n (это следует из того, что имеем последовательность 20 , 21 , 22 ,…,2n-1, 2n, и по формуле суммы геометрической прогрессии получаем
, где ν(n) – число равных 1 битов в двоичном представлении n (это следует из того, что имеем последовательность 20 , 21 , 22 ,…,2n-1, 2n, и по формуле суммы геометрической прогрессии получаем  ). Так, например: ν(27) = ν(11011) = 4, тогда J(J(…J(27)…)) =24 −1=15
). Так, например: ν(27) = ν(11011) = 4, тогда J(J(…J(27)…)) =24 −1=15
|
Теперь давайте вернемся к нашему первоначальному предположению, что J(n) =  при четном n. Вообще-то это неверно, но мы выясним, когда это верно: J(n) =
при четном n. Вообще-то это неверно, но мы выясним, когда это верно: J(n) =  , тогда 2k+1 =
, тогда 2k+1 =  => k =
=> k =  . Если число k = =
. Если число k = =  целое, то n= 2m + k будет решением, т.к. k < 2m. Нетрудно убедиться, что (2m − 2) кратно 3, когда m нечетно, но не когда m четно. Действительно, если m – нечетно, то 2m − 2 = 22k+1 − 2 = 2(4k − 1). Докажем методом математической индукции, что (4k − 1) делится на три (где
целое, то n= 2m + k будет решением, т.к. k < 2m. Нетрудно убедиться, что (2m − 2) кратно 3, когда m нечетно, но не когда m четно. Действительно, если m – нечетно, то 2m − 2 = 22k+1 − 2 = 2(4k − 1). Докажем методом математической индукции, что (4k − 1) делится на три (где 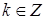 ):
):
1) База: k=1, 4−1=3, три делится на три (верно);
2) Индуктивный переход: пусть верно для всех чисел t ≤(k−1), т.е (4t−1) делится на три. Докажем для t=k:
4k − 1 = 4(4k-1 − 1) + 3  (4k-1 − 1) делится на три, и 3 делится на три => (4к−1) делится на три.
(4k-1 − 1) делится на три, и 3 делится на три => (4к−1) делится на три.
Таким образом, показали, что для m – нечетного (2m − 2) делится на 3.
Теперь покажем, что при m – четном (2m − 2) не делится на 3. Предположим противное: пусть (2m − 2) делится на 3 при четном m, тогда  , числа 2 и 3 взаимнопростые, следовательно, (
, числа 2 и 3 взаимнопростые, следовательно, ( ) должно делится на 3, т.е.
) должно делится на 3, т.е.  =3q
=3q 
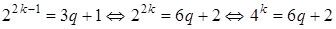 , но
, но  , a
, a  , т.е. получили, что
, т.е. получили, что 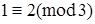 , а это не верно. Следовательно, наше предположение не верно и 2m − 2 не делится на 3 при четном m.
, а это не верно. Следовательно, наше предположение не верно и 2m − 2 не делится на 3 при четном m.
Таким образом, имеем бесконечно много решений уравнения J(n) =  , и первые такие:
, и первые такие:
| m | k | N= 2m + k | J(n) =2k+1= 
| n (двоичное) |
Правый крайний столбец содержит двоичные числа, циклический сдвиг которых на одно позицию влево дает тот же самый результат, что и обычный сдвиг на одну позицию вправо (деление пополам).
Далее обобщим J - функцию, т.е. рассмотрим рекуррентность схожую с (7), но с другими константами: α, β и γ; найдем решение в замкнутой форме.
f(1) = α,
f(2n) = 2f(n) + β при n ≥ 1, (10)
f(2n + 1) = 2f(n) + γ при n ≥ 1.
Составим таблицу для малых значений n:
 Анализируя таблицу можно сделать предположение, что коэффициенты при α равны наибольшим степеням 2, не превосходящим n; между последовательностями 2 коэффициенты при β уменьшаются на 1 вплоть до 0, а при γ увеличиваются на 1, начиная с 0. Если выразить f(n) в виде:
Анализируя таблицу можно сделать предположение, что коэффициенты при α равны наибольшим степеням 2, не превосходящим n; между последовательностями 2 коэффициенты при β уменьшаются на 1 вплоть до 0, а при γ увеличиваются на 1, начиная с 0. Если выразить f(n) в виде:
f(n) = A(n)∙α + B(n)∙β + C(n)∙γ (11)
то, по-видимому,
A(n) = 2m ,
B(n) = 2m −1−k, (12)
С(n) = k.
Здесь n = 2m + k и 0 ≤ k < 2m при n ≥ 1.
Докажем соотношения (11) и (12).
Докажем (11) методом математической индукции по числу n и при этом будем полагать, что (12) выполняется.
1) База: n=1=20+0 (m=k=0), f(1) =A(1)∙α+B(1)∙β+C(1)∙γ= =20∙α+(20−1−0)∙β+0∙γ = α (верно);
2) Индуктивный переход: пусть верно для всех чисел t ≤ (n–1), т.е. выполняется равенство f(t) = A(t)∙α + B(t)∙β + C(t)∙γ. Докажем для t=n:
a) если n – четное, тогда k тоже четное, т.е. k = 2t, и f(n) = f(2m+2t) = =f(2(2m-1 + t))  2∙f(2m-1 + t)+β
2∙f(2m-1 + t)+β  2∙(A(2m-1 + t)∙α + B(2m-1 + t)∙β + C(2m-1 + +t)∙γ) + β
2∙(A(2m-1 + t)∙α + B(2m-1 + t)∙β + C(2m-1 + +t)∙γ) + β 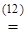 2(2m-1∙α + (2m-1−1−t)∙β + t∙γ) + β = 2m∙α + (2m−1−2t)∙β + 2t∙γ = 2m∙α+ + (2m−1−k)∙β + k∙γ = A(n)∙α + B(n)∙β + C(n)∙γ;
2(2m-1∙α + (2m-1−1−t)∙β + t∙γ) + β = 2m∙α + (2m−1−2t)∙β + 2t∙γ = 2m∙α+ + (2m−1−k)∙β + k∙γ = A(n)∙α + B(n)∙β + C(n)∙γ;
b) если n - нечетное, тогда k тоже нечетно, т.е. k=2t+1, и f(n) = =f(2m+2t+1) = f(2(2m-1 + t)+1)  2∙f(2m-1 + t)+ γ
2∙f(2m-1 + t)+ γ  2∙(A(2m-1 + t)∙α + B(2m-1 + +t)∙β + C(2m-1 + t)∙γ) + γ
2∙(A(2m-1 + t)∙α + B(2m-1 + +t)∙β + C(2m-1 + t)∙γ) + γ  2(2m-1∙α + (2m-1−1−t)∙β + t∙γ) + γ = 2m∙α + +(2m−1−(2t+1))∙β + (2t+1)∙γ = 2m∙α+ + (2m−1−k)∙β + k∙γ = A(n)∙α + B(n)∙β + C(n)∙γ.
2(2m-1∙α + (2m-1−1−t)∙β + t∙γ) + γ = 2m∙α + +(2m−1−(2t+1))∙β + (2t+1)∙γ = 2m∙α+ + (2m−1−k)∙β + k∙γ = A(n)∙α + B(n)∙β + C(n)∙γ.
Из пунктов 1 и 2 следует: для n ≥ 1 f(n) = A(n)∙α + B(n)∙β + C(n)∙γ.
Теперь докажем (12) в предположении, что (11) выполняется.
Если n - четное, тогда по соотношению (10) f(2n) = 2f(n) + β. Подставляя в данное равенство соотношение (11) получим:
A(2n)∙α + B(2n)∙β + C(2n)∙γ = 2(A(n)∙α + B(n)∙β + C(n)∙γ) + β
(A(2n) − 2A(n))∙α + (B(2n) − 2B(n)−1)∙β + (C(2n) − 2C(n))∙γ = 0
Теперь подставим соотношение (12) в данное равенство и посмотрим, будет ли оно выполнятся: т.к. n = 2m + k => 2n = 2m+1+2k, тогда A(2n) = 2m+1 , B(2n)=2m+1−1−2k, С(n)=2k. Подставляем: (2m+1 −2∙2m)∙α + +(2m+1−1−2k−2(2m−1−k)−1)∙β + (2k −2k)∙γ = 0  0∙α + 0∙β + 0∙γ = 0, получили 0=0 (верно);
0∙α + 0∙β + 0∙γ = 0, получили 0=0 (верно);
Если n - нечетное, тогда по соотношению (10) f(2n+1) = 2f(n) + γ. Снова подставляя в данное равенство соотношение (11) получим:
A(2n+1)∙α + B(2n+1)∙β + C(2n+1)∙γ = 2(A(n)∙α + B(n)∙β + C(n)∙γ) + γ
(A(2n+1) − 2A(n))∙α + (B(2n+1) − 2B(n))∙β + (C(2n+1) − 2C(n)−1)∙γ = 0
Теперь подставим соотношение (12) в данное равенство и посмотрим, будет ли оно выполнятся: n = 2m + k => 2n+1 = 2m+1+2k+1, тогда A(2n+1) = 2m+1 , B(2n+1) = 2m+1 −1−(2k+1), С(n+1) = 2k+1. Подставляем: (2m+1 −2∙2m)∙α + +(2m+1−2−2k−2(2m−1−k))∙β + (2k+1 −2k−1)∙γ=0  0∙α + 0∙β + 0∙γ = 0, получили 0=0 (верно).
0∙α + 0∙β + 0∙γ = 0, получили 0=0 (верно).
Таким образом, мы показали, что соотношения (11) и (12) верные.
Выше было показано, что J – рекуррентность имеет решение в двоичной записи: J((bm bm-1 … b1 b0)2) = (bm-1 … b1 b0 bm)2, где bm = 1. Можно показать, что и обобщенная рекуррентность (10) имеет похожее решение.
Запишем соотношение (10) следующим образом:
|
f(2n + j) = 2f(n) + βj при j = 0, 1 и n ≥ 1,
если положить β0 = β и β1 = γ. Тогда:
f((bm bm-1 … b1 b0)2) = 2f((bm bm-1 … b1)2) + βb  = 4f((bmbm-1…b2)2)+2βb
= 4f((bmbm-1…b2)2)+2βb  +βb
+βb  = =…=2mf((bm)2)+2m-1βb
= =…=2mf((bm)2)+2m-1βb  + … + 2βb
+ … + 2βb  +βb
+βb  = 2m α + 2m-1βb
= 2m α + 2m-1βb  + … + 2βb
+ … + 2βb  +βb
+βb  .
.
Если мы расширим систему счисления с основанием 2 таким образом, что в ней допустимы произвольные числа, а не только 0 и 1, тогда предыдущий вывод означает, что
f((bm bm-1 … b1 b0)2) = (α βb  βb
βb  … βb
… βb  βb
βb  )2 (16)
)2 (16)
Итак, изменение системы счисления привело нас к компактному решению (16) обобщенной рекуррентности (15).
Глава 2
Решение задач
Задача 1. То, что все лошади одной масти, можно доказать индукцией по числу лошадей в определенном табуне. Вот так:
«Если существует только одна лошадь, то она своей масти, так что база индукции тривиальна. Для индуктивного перехода предположим, что существует n лошадей (с номерами от 1 до n). По индуктивному предположению лошади с номерами от 1 до n−1 одинаковой масти, и, аналогично, лошади с номерами от 2 до n имеют одинаковую масть. Но лошади посередине с номерами от 2 до n−1 не могут изменять масть в зависимости от того, как они сгруппированы, - это лошади, а не хамелеоны. Поэтому в силу транзитивности лошади с номерами от 1 до n также должны быть одинаковой масти. Таким образом, все n лошадей одинаковой масти. Что и требовалось доказать».
Есть ли ошибка в приведенном рассуждении и, какая именно?
Решение. Ошибка в данном рассуждении есть, и она заключается в доказательстве по индуктивному предположению. Для доказательства того, что n лошадей имеют одинаковою масть, используется пересечение двух множеств от 1 до n−1 и от 2 до n, но для n = 2 этого пересечения нет. Поэтому, если есть две лошади, имеющие разную масть, то утверждение неверно. Если же любые две лошади имеют одинаковую масть, то доказательство будет верным для любого n.
Задача 2. Найдите кратчайшую последовательность перекладываний, перемещающих башню из n дисков с левого колышка А на правый колышек B, если прямой обмен между А и B запрещен. (Каждое перекладывание должно производиться через средний колышек. Как обычно, больший диск нельзя класть на меньший.)
|
|


|

 Решение.
Решение.
 | |||||
 |  |
Пусть Fn - минимальное число перекладываний, необходимых для перемещения n дисков с одного колышка на другой через колышек С.
Рассмотрим крайние случаи: F0=0, F1=2, F2=8, F3=26. Эксперимент с тремя дисками дает ключ к общему правилу перемещения n дисков: сначала мы перемещаем (n−1) меньших дисков на колышек B (что требует Fn-1 перекладываний), затем перекладываем самый большой диск на колышек С (одно перекладывание), потом помещаем (n−1) меньших дисков на колышек А (еще Fn-1 перекладываний), затем перекладываем самый большой диск на колышек B (одно перекладывание), и, наконец, помещаем (n−1) меньших дисков на колышек B (еще Fn-1 перекладываний). Таким образом, n дисков (при n>0) можно переместить самое большое за 3Fn-1+2 перекладываний (т.е. достаточно перекладываний): Fn ≤ 3Fn-1+2.
Сейчас покажем, что необходимо 3Fn-1+2 перекладываний. На двух этапах мы обязаны переместить самый большой диск. Когда мы это делаем, (n−1) меньших дисков должны находиться на одном колышке (А или B), а для того чтобы собрать их вместе, потребуется, по меньшей мере, Fn-1 перекладываний. Самый большой диск можно перекладывать и более одного раза. Следовательно, Fn ≥ 3Fn-1+2.
Эти два неравенства вместе с тривиальным решением при n=0 дают рекуррентное соотношение:
F0=0
Fn = 3Fn-1+2 при n>0
Решим данное соотношение.
Первый способ решения (угадывание правильного решения с последующим доказательством, что наша догадка верна). Вычислим: F1=2=31 −1, F2=32 −1, F3=33 −1. Из этого можно сделать предположение, что
Fn = 3n −1 при n≥0.
Докажем методом математической индукции по числу n:
1) База: n=0, F0=30–1=1–1=0 (верно);
2) Индуктивный переход: пусть доказано для всех чисел t ≤ (n–1). Докажем для t=n: Fn= 3Fn-1+2  3(3n-1−1)+2 = 3n − 1.
3(3n-1−1)+2 = 3n − 1.
Из пунктов 1 и 2 следует: при n≥0 Fn = 3n − 1.
Второй способ решения.
К обеим частям соотношения (1) прибавим 1:
F0+1 = 1,
Fn+1 = 3Fn-1+3 при n>0.
Обозначим Un = Fn+1, тогда получим: U0 = 1, Un = 3Un-1 при n>0.
Решением этой рекурсии есть Un= 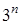 ; следовательно, Fn =
; следовательно, Fn = 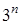 −1.
−1.
В дальнейшем мы не будем показывать достаточное и необходимое условие в решении подобных задач, а сразу будем описывать получение нужного равенства. Это связано, во-первых, с тем, что достаточное и необходимое условие показывается аналогично тому, как это сделано в данной задаче, а во-вторых, в виду ограниченности объема дипломной работы.
Задача 3. Покажите, что в процессе перемещения башни при ограничениях из предыдущего упражнения нам встретятся все допустимые варианты размещения n дисков на трех колышках.


 Решение. Занумеруем диски
Решение. Занумеруем диски
 |




Существует (в соответствии с условиями задачи) только три возможных расположения каждого диска на одном из колышков: либо на первом колышке (А), либо на втором колышке (B), либо на третьем колышке (С). Это будут перестановки длины n из трех элементов. Например, 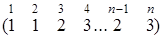 .
.
 Число перестановок длины k из n элементов:
Число перестановок длины k из n элементов:  . Следовательно, для нашего случая
. Следовательно, для нашего случая  , т.е.
, т.е. 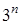 – это все возможные различные расположения n дисков на трех колышках.
– это все возможные различные расположения n дисков на трех колышках.
В предыдущей задаче было показано, что наименьшее число перекладываний с колышка А на колышек B через колышек С равно 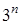 −1. Таким образом, каждый раз перекладывая диск с одного колышка на другой, мы получаем все допустимые расположения n дисков на трех колышках (т.к. мы не перекладываем один диск с одного колышка на другой по несколько раз)
−1. Таким образом, каждый раз перекладывая диск с одного колышка на другой, мы получаем все допустимые расположения n дисков на трех колышках (т.к. мы не перекладываем один диск с одного колышка на другой по несколько раз)
Задача 4. Имеются ли какие-нибудь начальная и конечная конфигурации из n дисков на трех колышках, которые требуют более чем  −1 перекладываний, чтобы получить одну из другой по исходным правилам Люка?
−1 перекладываний, чтобы получить одну из другой по исходным правилам Люка?
Решение. Докажем методом математической индукции, что любая начальная и конечная конфигурации из n дисков на трех колышках требуют не более чем  −1 перекладываний, чтобы получить одну из другой по исходным правилам Люка.
−1 перекладываний, чтобы получить одну из другой по исходным правилам Люка.
1) База: если n=1, то требуется одно перекладывание, тогда 1 ≤ 20−1 (верно);
2) Индуктивный переход: пусть для любой начальной и конечной конфигурации из n−1 дисков на трех колышках требуется не более чем  −1 перекладываний. Докажем для n дисков:
−1 перекладываний. Докажем для n дисков:
· если начальная и конечная конфигурации не предполагают перекладывание самого большого нижнего диска, тогда мы перекладываем только n−1 верхних дисков, а по индуктивному предположению для этого потребуется не более чем  −1 перекладываний;
−1 перекладываний;
· если начальная и конечная конфигурации предполагают перекладывание самого большого нижнего диска, тогда мы перекладываем n−1 верхних дисков, а по индуктивному предположению для этого будет достаточно  −1 перекладываний (т.е. n−1 верхних дисков разместили на одном колышке), затем перекладываем самый большой диск (одно перекладывание), и снова перекладываем n−1 верхних дисков, как требует конечная конфигурация (достаточно
−1 перекладываний (т.е. n−1 верхних дисков разместили на одном колышке), затем перекладываем самый большой диск (одно перекладывание), и снова перекладываем n−1 верхних дисков, как требует конечная конфигурация (достаточно  −1 перекладываний). Таким образом, получили, что потребуется не более чем
−1 перекладываний). Таким образом, получили, что потребуется не более чем  −1 + 1+
−1 + 1+  −1=
−1=  перекладываний.
перекладываний.
Из всего этого следует, что не существует начальной и конечной конфигурации из n дисков на трех колышках требующей более чем  −1 перекладываний, чтобы получить одну из другой по исходным правилам Люка.
−1 перекладываний, чтобы получить одну из другой по исходным правилам Люка.
Задача 5. Так называемая «диаграмма Венна» с тремя пересекающимися окружностями часто приводится для иллюстрации восьми возможных подмножеств, связанных с тремя заданными множествами:
 Можно ли проиллюстрировать четырьмя пересекающимися окружностями шестнадцать возможностей, которые возникают в связи с четырьмя заданными множествами?
Можно ли проиллюстрировать четырьмя пересекающимися окружностями шестнадцать возможностей, которые возникают в связи с четырьмя заданными множествами?
 Решение. Так как три пересекающиеся окружности иллюстрируют восемь различных подмножеств, то для того чтобы получить шестнадцать возможных подмножеств надо, чтобы четвертая окружность пересекала все восемь множеств. Но такого быть не может. Две произвольные окружности могут иметь не более двух точек пересечения, поэтому, проводя четвертую окружность, мы сможем получить максимум шесть дополнительных подмножеств. Так как возможно только два расположения четвертой окружности относительно трех данных окружностей: 1) четвертая окружность пересекает внешнее подмножество (рис. 1); 2) четвертая окружность лежит внутри трех пересекающихся окружностей (рис.2).
Решение. Так как три пересекающиеся окружности иллюстрируют восемь различных подмножеств, то для того чтобы получить шестнадцать возможных подмножеств надо, чтобы четвертая окружность пересекала все восемь множеств. Но такого быть не может. Две произвольные окружности могут иметь не более двух точек пересечения, поэтому, проводя четвертую окружность, мы сможем получить максимум шесть дополнительных подмножеств. Так как возможно только два расположения четвертой окружности относительно трех данных окружностей: 1) четвертая окружность пересекает внешнее подмножество (рис. 1); 2) четвертая окружность лежит внутри трех пересекающихся окружностей (рис.2).
 рис.1 рис.2
рис.1 рис.2
 |
Если добавленная окружность пересекает внешнее множество, то она не сможет пересечь как минимум два внутренних множества (зависит от радиуса окружности).
Если добавленная окружность лежит внутри трех пересекающихся окружностей, то она не пересекает внешнее множество и как минимум одно внутреннее множество.
Таким образом, получили, что четырьмя окружностями можно проиллюстрировать максимум 14 (8+6=14) возможных подмножеств.
Задача 6. Некоторые из областей, очерчиваемых n прямыми на плоскости, бесконечны, в то время как другие конечны. Какое максимально возможное число конечных областей?
Решение. Пусть  - максимальное число возможных конечных областей, очерчиваемых n прямыми.
- максимальное число возможных конечных областей, очерчиваемых n прямыми.



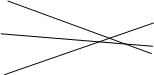
 Рассмотрим частные случаи (при условии, что n-я прямая не параллельна никакой другой прямой (следовательно, она пересекает каждую из них), и не проходит ни через одну из имеющихся точек пересечения (следовательно, она пересекает каждую из прямых в различных местах)):
Рассмотрим частные случаи (при условии, что n-я прямая не параллельна никакой другой прямой (следовательно, она пересекает каждую из них), и не проходит ни через одну из имеющихся точек пересечения (следовательно, она пересекает каждую из прямых в различных местах)):
 | |||||||||||||
 | |||||||||||||
 |  | ||||||||||||
 | |||||||||||||
 |
| ||||||||||||


Обобщая, приходим к следующему выводу: новая n-я прямая (при n≥3) пересекает n–1 старых прямых в n−1 различных точках, следовательно, получаем n областей и две крайние из которых бесконечны. Таким образом, получили следующее рекуррентное соотношение:
|

Решим данное соотношение.

|

(Здесь Ln =  + 1- максимальное число областей, на которые плоскость делится n прямыми).
+ 1- максимальное число областей, на которые плоскость делится n прямыми).
Докажем полученное равенство методом математической индукции по числу n:
1) База: n=0,  (верно);
(верно);
2) Индуктивный переход: пусть доказано для всех чисел t ≤ (n–1). Докажем для t=n: 
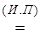
 =
=  =
=
= 
Из пунктов 1 и 2 следует: при n ≥ 0 
Задача 7. Пусть H(n) = J(n+1)−J(n). В силу уравнения (7) (см. теорию) H(2n) = J(2n+1)− J(2n) 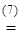 (2J(n)+1) − (2J(n)−1) = 2, a H(2n+1) = J(2n+2)− −J(2n+1) = (2J(n+1)−1)−(2J(n)+1) = 2H(n)−2 при всех n≥1. Поэтому представляется возможным доказать индукцией по n, что H(n)=2 при всех n. Что здесь не верно?
(2J(n)+1) − (2J(n)−1) = 2, a H(2n+1) = J(2n+2)− −J(2n+1) = (2J(n+1)−1)−(2J(n)+1) = 2H(n)−2 при всех n≥1. Поэтому представляется возможным доказать индукцией по n, что H(n)=2 при всех n. Что здесь не верно?
Решение. Ошибка заключается в том, что в данном рассуждении хотят доказать по индукции, что H(n)=2 при всех n (показали, что данное равенство выполняется для чисел вида 2n и 2n+1, т.к. любое натуральное число можно представить в таком виде), но при этом не проверили базу индукции (т.е. когда n принимает свое наименьшее значение: n = 1).
H(1) = J(2) − J(1) = 2J(1) −1 − J(1) = 2∙1−1−1 = 0 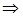 H(1)
H(1)  2
2  база индукции не выполняетс
база индукции не выполняетс
