Точка, как математическое понятие, не имеет размеров. Очевидно, если объект проецирования является пульмерным объектом, то говорить о его проецировании бессмысленно.
В геометрии под точкой целесообразно принимать физический объект, имеющий линейные измерения. Условно за точку можно принять шарик с бесконечно малым радиусом. При такой трактовке понятия точки можно говорить о ее проекциях.
|
Рис.9 Рис.10
При построении ортогональных проекций точки следует руководствоваться первым инвариантным свойством ортогонального проецирования: ортогональная проекция точки есть точка.
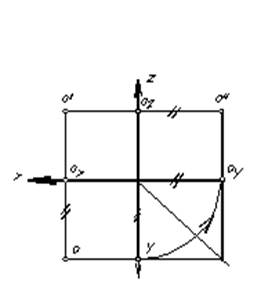
Положение точки в пространстве определяется тремя координатами: X, Y, Z, показывающие величины расстояний, на которые точка удалена от плоскостей проекций. Чтобы определить эти расстояния, достаточно определить точки встречи этих прямых с плоскостями проекций и измерить соответствующие величины, которые укажут соответственно значения абсциссы X, ординаты Y и аппликаты Z точки (рис. 10).
Проекцией точки является основание перпендикуляра, опущенного из точки на соответствующую плоскость проекций. Горизонтальной проекцией точки а называют прямоугольную проекцию точки на горизонтальной плоскости проекций, фронтальной проекцией а / – соответственно на фронтальной плоскости проекций и профильной а// – на профильной плоскости проекций.
Прямые Аа, Аa / и Аa // называются проецирующими прямыми. При этом прямую Аа, проецирующую точку А на горизонтальную плоскость проекций, называют горизонтально- проецирующей прямой, Аa / и Аa // - соответственно: фронтально и профильно-проецирущими прямыми.
Две проецирующие прямые, проходящие через точку А определяют плоскость, которую принято называть проецирующей.
При преобразовании пространственного макета, фронтальная проекция точки А – а / остается на месте, как принадлежащая плоскости, которая не меняет своего положения при рассматриваемом преобразовании. Горизонтальная проекция – а вместе с горизонтальной плоскостью проекции повернется по направлению движения часовой стрелки и расположится на одном перпендикуляре к оси Х с фронтальной проекцией. Профильная проекция - a // будет вращаться вместе с профильной плоскостью и к концу преобразования займет положение, указанное на рисунке 10. При этом - a // будет принадлежать перпендикуляру к оси Z, проведенному из точки а / и будет удалена от оси Z на такое же расстояние, на какое горизонтальная проекция а удалена от оси Х. Поэтому связь между горизонтально и профильной проекциями точки может быть установлена с помощью двух ортогональных отрезков ааy и аy a // и сопрягающей их дуги окружности с центром в точке пересечения осей (О – начало координат). Отмеченной связью пользуются для нахождения недостающей проекции (при двух заданных). Положение профильной (горизонтальной) проекции по заданным горизонтальной (профильной) и фронтальной проекциям может быть найдено с помощью прямой, проведенной под углом 450 из начала координат к оси Y (эту биссектрису называют прямой k – постоянной Монжа). Первый из указанных способов предпочтителен, как более точный.
Из этого следует:
1. Точка в пространстве удалена:
от горизонтальной плоскости H на величину заданной координаты Z,
от фронтальной плоскости V на величину заданной координаты Y,
от профильной плоскости W на величину координаты. X.
2. Две проекции любой точки принадлежат одному перпендикуляру (одной линии связи):
горизонтальная и фронтальная – перпендикуляру к оси X,
горизонтальная и профильная – перпендикуляру к оси Y,
фронтальная и профильная – перпендикуляру к оси Z.
3. Положение точки в пространстве вполне определяется положением ее двух ортогональных проекций. Из этого следует – по двум любым заданным ортогональным проекциям точки всегда иожно построить недостающую ее третью проекцию.


Рис. 11 Рис. 12
Если точка имеет три определенные координаты, то такую точку называют точкой общего положения. Если у точки одна или две координаты имеют нулевое значение, то такую точку называют точкой частного положения.
На рисунке 11 дан пространственный чертеж точек частного положения, на рисунке 12 – комплексных чертеж (эпюр) этих точек. Точка А принадлежит фронтальной плоскости проекций, точка В – горизонтальной плоскости проекций, точка С – профильной плоскости проекций и точка D – оси абсцисс (Х).
При построении проекций прямой следует исходить из инвариантного свойства ортогонального проецирования, что проекция прямой есть прямая.

|
Рис.13 Рис. 14
При ортогональном проецировании на плоскость прямая, не перпендикулярна- плоскости проекций, проецируется в прямую. Поэтому, для проецирования отрезка прямой достаточно найти проекции концов отрезка.
Наглядное (пространственное) изображение отрезка АВ показано на рисунке 13 и его ортогональное проецирование на три плоскости проекций – на рисунке 14. Отрезок АВ, определяющий прямую, занимает произвольное (общее) положение по отношению к плоскостям проекций (углы наклона прямой к плоскостям проекций произвольные, но отличные от 00 и 900). Такая прямая называется прямой общего положения.
Отметим, что если какая-либо точка принадлежит прямой, то ее проекции принадлежат соответственным проекциям данной прямой.