Московский Педагогический Государственный Университет
Биолого-химический факультет
Реферат по истории и философии науки
История изучения динамики популяций
Выполнил: студент 6 курса магистратуры
Фомин А. В.
Проверила: д. б. н. профессор
Кузнецова Н. А.
Москва 2011
Содержание
На разных уровнях развития живой материи продукционные процессы проявляют себя по-разному, но их феноменологическое описание всегда включает рождение, рост, взаимодействие с внешней средой, в том числе с другими особями своего вида или других видов, смерть особей. Именно это обстоятельство позволяет применять сходный математический аппарат для описания моделей роста и развития у таких, казалось бы, удаленных друг от друга по лестнице уровней организации живой материи, как клеточная популяция и сообщество видов в экосистеме.
Описание изменения численности популяции во времени составляет предмет популяционной динамики. Популяционная динамика является частью биологии математической, наиболее продвинутой в смысле формального математического аппарата, своего рода "математическим полигоном" для проверки теоретических идей и представлений о законах роста и эволюции биологических видов, популяций, сообществ. Возможность описания популяций различной биологической природы одинаковыми математическими соотношениями обусловлена тем, что с динамической точки зрения, рост и отбор организмов в процессе эволюции происходит по принципу "Кинетического совершенства" (Шноль, 1979)
Преимущества математического анализа любых, в том числе популяционных, процессов, очевидны. Математическое моделирование не только помогает строго формализовать знания об объекте, но иногда (при хорошей изученности объекта) дать количественное описание процесса, предсказать его ход и эффективность, дать рекомендации по оптимизации управления этим процессом. Это особенно важно для биологических процессов, имеющих прикладное и промышленное значение - биотехнологических систем, агробиоценозов, эксплуатируемых природных экосистем, продуктивность которых определяется закономерностями роста популяций живых организмов, представляющих собой "продукт" этих биологических систем.
Ряд Фибоначчи
Постановка математических задач в терминах популяционной динамики восходит к глубокой древности. Человеку свойственно рассуждать о предметах, жизненно ему близких, и что может быть ближе, чем законы размножения популяций - людей, животных, растений.
Первая дошедшая до нас математическая модель динамики популяций приводится в книге "Трактат о счете" "Liber abaci", датированной 1202 годом, написанной крупнейшим итальянским ученым Леонардо Фибоначчи - Леонардо из Пизы, (предположительно 1170-1240). В этой книге, представляющей собой собрание арифметических и алгебраических сведений того времени и впоследствии распространившейся в списках по всей Европе, рассматривается следующая задача. "Некто выращивает кроликов в пространстве, со всех сторон обнесенном высокой стеной. Сколько пар кроликов рождается в один год от одной пары, если через месяц пара кроликов производит на свет другую пару, а рожают кролики, начиная со второго месяца после своего рождения.". Решением задачи является ряд чисел:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,... (1)
(Сам Леонардо опустил первый член ряда). Два первых числа соответствуют первому и второму месяцу размножения. 12 последующих - месячному приросту поголовья кроликов. Каждый последующий ряд равен сумме двух предыдущих. Ряд (1) вошел в историю как ряд Фибоначчи, а его члены - чисел Фибоначчи. Это первая известная в Европе рекурсивная последовательность чисел (в которой соотношение между двумя или более членами ряда может быть выражена в виде формулы). Рекуррентная формула для членов ряда Фибоначчи была записана французским математиком Альбертом Гирером в 1634 г.
Здесь U представляет собой член последовательности, а нижний индекс - его номер в ряду чисел. В 1753 г. математик из Глазго Роберт Симпсон заметил, что при увеличении порядкового номера членов ряда отношение последующего члена к предыдущему приближается к числу a, называемому "Золотым сечением", равному 1,6180..., или. В 19 веке о свойствах ряда Фибоначчи и его связи с Золотым сечением много писал французский математик Эдуард Лукас. С тех пор естествоиспытатели наблюдают его закономерности в расположения чешуек на шишках, лепестков в цветке подсолнуха, в спиральных образованиях ракушек моллюсков и других творениях природы. Ряд Фибоначчи и его свойства также используются в вычислительной математике при создании специальных алгоритмов счета.
Уравнение экспоненциального роста.
Второй всемирно известной математической моделью, в основу которой положена задача о динамике численности популяции, является классическая модель неограниченного роста – геометрическая прогрессия в дискретном представлении,

или экспонента, - в непрерывном
 (2)
(2)
Модель предложена Мальтусом в 1798 г. в его классическом труде "О росте народонаселения". Томас Роберт Мальтус (1766-1834) известный английский демограф и экономист, обратил внимание на тот факт, что численность популяции растет по экспоненте (в геометрической прогрессии), в то время как производство продуктов питания растет со временем линейно (в арифметической прогрессии), из чего сделал справедливый вывод, что рано или поздно экспонента обязательно "обгонит" линейную функцию, и наступит голод. На основании этих выводов Мальтус говорит о необходимости ввести ограничения на рождаемость, в особенности для беднейших слоев общества. "Экономический пессимизм", следующий из прогнозов предложенной им модели, в основу которой положен анализ эмпирических данных, Мальтус противопоставлял модным в начале 19 века оптимистическим идеям гуманистов: Жана Жака Руссо, Уильяма Годвина и других, предсказывающих человечеству грядущее счастье и процветание. Можно говорить о том, что Мальтус был первым ученым "алармистом", который на основании результатов моделирования "бил тревогу" и предупреждал человечество об опасности следования развитию по используемым ранее сценариям прогресса. Во второй половине 20 века такую "алармистскую" роль сыграли работы Римского клуба, и в первую очередь "модель глобального роста" Дж. Форрестера. (см. Экология математическая).
Обсуждению важности вывода Мальтуса для популяционной динамики Дарвин посвятил несколько страниц своего дневника, указывая, что поскольку ни одна популяция не размножается до бесконечности, должны существовать факторы, препятствующие такому неограниченному размножению. Среди этих факторов может быть нехватка ресурса (продовольствия), вызывающая конкуренцию внутри популяции за ресурс, хищничество, конкуренция c другими видами. Результатом является замедление скорости роста популяции и выход ее численности на стационарный уровень.
Ограниченный рост
Впервые системный фактор, ограничивающий рост популяции, описал Ферхюльст в уравнении логистического роста (1848):
 (3)
(3)
Это уравнение обладает двумя важными свойствами. При малых х численность х возрастает экспоненциально (как в уравнении 2) при больших - приближается к определенному пределу К. Эта величина, называемая емкостью популяции, определяется ограниченностью пищевых ресурсов, мест для гнездования, многими другими факторами, которые могут быть различными для разных видов. Таким образом емкость экологической ниши представляет собой системный фактор, который определяет ограниченность роста популяции в данном ареале обитания.
Уравнение (3) можно также переписать в виде:
 (4)
(4)
Здесь - коэффициент внутривидовой конкуренции (за пищевой ресурс, убежища и т.п. Уравнение (3) можно решить аналитически. Решение имеет вид:
 (5)
(5)
Формула (5) описывает кинетическую кривую, то есть зависимость численности популяции от времени. Примеры экспериментально наблюдаемой динамики популяций, развивающихся по логистическому закону, приведены на рис. 1а,б.

Рис.1. Ограниченный рост. а. Динамика численности жука Rhizopertha dominica в 10-граммовой порции пшеничных зерен, пополняемых каждую неделю. Точки- экспериментальные данные, сплошная линия - логистическая кривая. б. Динамика численности водоросли Chlorella в культуре. Рисунки из [3].
На рис. 1а сплошной линией представлен график функции (5).Если выражение (5) продифференциировать два раза по t, увидим, что кривая x(t) имеет точку перегиба, с координатами:

Ордината представляет собой половину максимальной численности, а абсцисса зависит как от емкости популяции K, так и от константы собственной скорости роста r - чем выше генетические возможности популяции, тем скорее наступает перегиб на кривой численности.
Логистическая модель Ферхюльста (3) оказалось не менее замечательной, чем ряд Фибоначчи. Исследование этого уравнения в случае дискретного изменения численности в популяциях с неперекрывающимися поколениями показало целый спектр возможных типов решений, в том числе колебательные изменения разного периода и вспышки численности. Рассмотрение модификации логистического уравнения с комплексными членами привело к новому классу объектов - множествам Мандельброта и Жолиа, имеющим фрактальную структуру Бенуа Мандельброт - создатель современной теории фракталов, родился в 1924 г. в Варшаве, в 1958 г. работал в США, с 1984 г. - профессор Гарвардского университета в Англии. Полученные им впервые компьютерные изображения множества

пробрели всемирную известность и были многократно воспроизведены в разных модификациях на компьютерах. Красота фрактальных изображений завораживает. (См. "Красота фракталов", М., 1995 - перевод с англ. книги: H.-O.Peitgen, P.H.Richer " The Beauty of Fractals",Springer, 1986).
К дискретному логистическому уравнению мы обратимся позднее, а сейчас вспомним тот биологический факт, что в природе популяции имеют не только максимальную численность, определяемую величиной экологической ниши K, но и минимальную критическую численность L. При падении численности популяции ниже этой критической величины из-за неблагоприятных условий, или в результате хищнического промысла, восстановление популяции становится невозможным.
Величина нижней критической плотности различна для разных видов. Исследования биологов показали, что она может составлять всего лишь пару особей на тысячу квадратных километров в случае ондатры, и сотни тысяч особей для американского странствующего голубя. Заранее трудно было предположить, что столь многочисленный вид уже перешел через критическую границу своей численности и обречен на вымирание. Например, для голубых китов критическая граница численности оказалась равной десяткам - сотням. Хищническое истребление этих гигантских животных привело к тому, что их осталось слишком мало в Мировом океане. И хотя охота на них давно запрещена, надежд на восстановление популяции голубых китов практически нет. Кривые показателей численности для трех видов китов приведены на рис. 2.

Рис.2. Динамика численности трех видов китов в мировом океане. По оси ординат отложен индекс численности - число убитых китов на 1 тыс. судо-тонно-суток. (Gulland, 1971)
Модели, описывающие как внутривидовую конкуренцию, определяющую верхнюю границу численности популяции, так и нижнюю критическую численность популяции, имеют два устойчивых стационарных решения. Одно из них - нулевое для начальных численностей, которые ниже наименьшей критической численности популяции. Другое равно K - емкости экологической ниши в случае, когда начальная численность выше наименьшей критической величины. Такими "триггерными" свойствами обладает нелинейное уравнение, предложенное А.Д.Базыкиным [1]
 (6)
(6)
В формуле (6) первый член в правой части описывает размножение двуполой популяции, скорость которого пропорциональна квадрату численности (вероятности встреч особей разного пола) для малых плотностей, и пропорциональна числу самок в популяции - для больших плотностей популяции. Второй член описывает смертность, пропорциональную численности, а третий - внутривидовую конкуренцию, подобно тому, как это было в логистическом уравнении (4).
Зависимости численности от времени и скорости прироста от численности представлены на рис. 3 (а,б). Кривые 1,-5 соответствуют различным начальным численностям. x=0 и x=K -устойчивые стационарные состояния, x=L -неустойчивое, разделяющее области влияния устойчивых состояний равновесия. Величины L и K различны для разных популяций и могут быть определены из наблюдений и экспериментов.
Из рисунка 3а видно, что скорость восстановления популяции после ее падения в силу промысла или неблагоприятных условий зависит от того, насколько близка новая начальная численность к опасной границе L. Если ущерб, нанесенный популяции невелик (меньше половины емкости экологической ниши) популяция быстро восстанавливается по кривой 1, не имеющей точки перегиба. В случае, когда численность оставшейся популяции близка к критической, восстановление происходит сначала очень медленно, популяция надолго "застревает" вблизи опасной границы", а затем уже, "набрав силы", более быстро выходит на устойчивый стационарный уровень K (кривая 3). Кривая 2 представляет промежуточный случай. Кривые 4, 5 иллюстрирует вырождение популяции в случае, когда начальная численность опустилась ниже критической границы. обращает на себя внимание сходства начальных участков кривых 3 и 5. Близость к опасной границе со стороны больших значений (3) и меньших (5) выражается в долгом пребывании системы в неопределенном состоянии, когда малые флуктуации могут легко "перебросить" систему через опасную границу в "благополучную" область возврата к стационарному значению K, или, наоборот, в область вымирания. В это время сторонний наблюдатель не сможет определить по форме кривой динамики численности, какая судьба ожидает систему. Для самих участников жизненной драмы - нахождения системы вблизи опасной границы - исход не очевиден. Важно понимать, что в этой ситуации чрезвычайно важны любые, даже очень малые усилия, направленные на преодоление критического барьера.
Именно популяции, численность которых близка к нижней критической численности, занесены в Красную книгу. Удастся ли перенести каждый конкретный вид на "Зеленые страницы", куда переносят виды, исчезновение которых удалось предотвратить, зависит от многих обстоятельств, в частности как от репродуктивных усилий вида, так и от усилий людей, спасающих эти виды.
Влияние запаздывания.
Уравнения, которые мы рассматривали до сих пор, предполагают, что процессы размножения и гибели происходят одновременно и популяция мгновенно реагирует на любое изменение внешних условий. Однако в реальности это не так. Всегда имеется некоторое запаздывание, которое вызвано несколькими причинами.
Развитие любой взрослой особи из оплодотворенного яйца требует определенного времени T. Поэтому если какое-нибудь изменение в окружающей среде, например, увеличение ресурса, вызовет внезапное повышение продуктивности взрослых особей, то соответствующе изменение численности произойдет лишь по прошествии времени T. Это означает, что уравнение
dx/dt=f(x), (7)
где x - численность взрослых особей, следует заменить уравнением:
dx/dt=f(xt--T) (8)
где xt--T - численность половозрелых особей в момент t-T.
В реальных популяциях интенсивность размножения и гибели различны в разных возрастных группах. Например, у насекомых откладывают яйца взрослые особи, а конкуренция наиболее выражена на личиночной стадии. Такие процессы, как отравление среды продуктами метаболизма, каннибализм и т.п. в наиболее сильной степени воздействуют на ранние возрастные стадии, а их интенсивность зависит от численности взрослых особей, т.е. отрицательное влияние на коэффициент естественного прироста оказывают особи предыдущего поколения. С учетом этих обстоятельств, логистическое уравнение (4) перепишется в виде:
dx/dt=x(r-xt-T) (9)
Наиболее распространенное и изученное в динамике популяций уравнение Хатчинсона учитывает тот факт, что особи размножаются лишь с определенного возраста, и имеет вид:
 (10)
(10)
Смысл модели (10) заключается в том, что уровень лимитирования системы зависит не только от общей численности популяции в данный момент времени t, определяемой емкостью среды, но и от количества половозрелых особей в момент времени t-T. Еще более точное уравнение, учитывающее распределение времени запаздывания:

Вид функции распределения времен запаздывания w(t-s) представлен на рис. 4. Такого типа уравнения могут иметь колебательные решения. Это легко проверить для простого линейного уравнения:

которое имеет периодическое решение  в широком диапазоне значений скоростей роста r и времени запаздывания T.
в широком диапазоне значений скоростей роста r и времени запаздывания T.
В технике хорошо известно, что запаздывание в регуляции системы может привести к возникновению колебаний переменных. Если система регулируется петлей обратной связи, в которой происходит существенная задержка, то весьма вероятно возникновение колебаний. Если продолжительность задержки в петле обратной связи больше собственного времени системы, могут возникнуть колебания с нарастающей амплитудой, нарушаются их период и фаза.
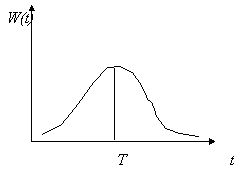
Рис.4. Модель динамики популяции с учетом распределения времен запаздывания. Типичный вид весовой функции w(t)
Дискретные модели популяций с неперекрывающимися поколениями
Даже в таких популяциях, где особи размножаются несколько лет подряд (млекопитающие и птицы, многолетние растения), наличие сезонов размножения вносит некоторое запаздывание в процессы регуляции численности. Если же взрослые особи, размножающиеся в данном году, редко или никогда не доживают до того, чтобы размножиться в будущем году, как, например, у однолетних растений, мелких грызунов, многих насекомых, это оказывает существенное влияние на динамику их численности. В этом случае уравнение (7) следует заменить уравнением
Nn+1=N(xn), (11)
где Nn - численность популяции в году n.
Наблюдения над динамикой численности показывают, что в таких системах при малых численностях N растет от одной генерации к другой, а при высоких - падает. Это свойство - резко расти при малых N и падать при больших, проявляется в экономике как закон "бумов и спадов". В таких случаях функция F - одноэкстремальная, вид ее изображен на рис. 5а.
Функция такого типа может быть описана с помощью различных формул. Ниболее широко распространена версия дискретного логистического уравнения, предложенная Мораном для численности насекомых (1950) и Рикером для рыбных популяций (1954):
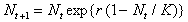 (12)
(12)
Здесь, как и в логистическом уравнении (3), r-константа собственной скорости роста, K - емкость экологической ниши популяции. Ход решения уравнения (12) можно наглядно продемонстрировать графически с помощью диаграммы и лестницы Ламерея. Точка пересечения биссектрисы первого координатного угла Nt+1=Nt и функции F(Nt) определяет равновесное состояние системы, аналогичное стационарному состоянию дифференциального уравнения. На рис. 5б показан способ нахождения значений Nt в последовательные моменты времени. Пусть в начальный момент времени N=N0. F(N0)=N1 задает значение численности в последующий момент времени t=1. Величина N1 в свою очередь определяет значение F(N1)=N2. И так далее. На рис. 5б изображен случай, когда траектория сходится к равновесному состоянию, совершая затухающие колебания.

Рис.5. Модели популяций с неперекрывающимися поколениями. а. Вид одноэкстремальной функции зависимости численности популяции в данный момент времени от численности в предыдущий момент времени. Nt+1=F(Nt); б. Определение значений численности популяции в последовательные моменты времени (см. текст) для дискретного аналога логистического уравнения (12).
В зависимости от крутизны графика функции F(N1) (кривые a,b,c,d на рис. 6) в системе могут возникать самые разнообразные режимы. С ростом r поведение усложняется. Монотонное стремление к равновесию (Рис.6а) сменяется колебательным (Рис.6б). При дальнейшем увеличении r (увеличении крутизны кривой F(N1)) возникают циклы - аналоги предельных циклов для систем дифференциальных уравнений (рис. 6 в,г). Если r еще больше растет - наблюдается квазистохастическое поведение - хаос. (рис. 6 д,е). Модели такого типа являются простейшими детерминированными объектами, демонстрирующими квазистохастическое поведение.
Квазистохастическим поведением могут обладать и переменные в непрерывных нелинейных автономных системах трех и более дифференциальных уравнений. Изображение детерминированного хаоса в популяции из трех видов: хишник - две жертвы представлено на рис.12. Таким образом, стохастичность может быть свойством, присущим самим детерминированным природным системам (Детерминированный хаос), и не зависит от того, какой математический аппарат, непрерывный или дискретны, используется.

Рис.6. Типы динамики численности в модели популяции с неперекрывающимися поколениями при разных значениях собственной скорости роста. а.- Монотонный рост; б.- Затухающие колебания; в.- двухточечный цикл; г.- четырехточечный цикл; д, е- квазистохастическое поведение.
Матричные модели популяций
Ч = П + Р – см – онк.
Доля = онк /Ч