Расчет каналов в безразмерных величинах.
Канал трапецеидального сечения проектируется при известном нормальном расходе Q, уклоне i, грунте. Форсированный расход определяется через коэффициент форсировки Qф=kфQ. Расчет ведется при равномерном движении в канале.
Требуется:
1. Определить по справочнику коэффициент шероховатости русла n и коэффициент заложения откоса m.
2. Определить размеры живого сечения (h0, b, β=b/h0) при Q по дополнительным условиям.
3. В случае, если kф>1, определить нормальную глубину hоф при Qф.
4. Определить среднюю скорость в сечении при Q и Qф и проверить возможность размыва.
| Исходные данные | Вариант 2 |
| Расход Q, м3/с | |
| Уклон i | 0,00015 |
| Грунт | Суглинок m=1,5 (связные грунты) Cрасч=0,1*105Па |
| Исходные данные | Вариант 2 |
| Коэффициент форсировки kф | 1,00 |
| Ширина b, м | - |
| Глубина h0, м | - |
| Относительная ширина β | βгн |
4m0=8.424
n=0.025 при <25 м3/с
Из первой таблицы находим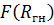 
и зная n находим Rгн.
По таблице 2 определяем: 
b=1,73*5,68=9,83=10 м
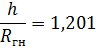
h0=1,201*1,73=2,08 м
R=0,899*1,73=1,56 м
Проверка на размыв: 
, 
по первой таблице Агроскина = 54,05
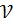доп=1,12 м/с.
Вывод: канал не размывается.
Не установившееся движение на участках на участках торможения.
В конце канала, рассчитанного в задаче 1, поставлено сооружение, которое нарушает равномерное движение. При этом устанавливается конечная глубина hкон и формируется подпора или спада.
hкон = 1,5
Требуется:
1. Определить критическую глубину hкр в канале при расходе Q.
2. Сравнивая h0, hкр, hкон выяснитьзону формирования кривой свободной поверхности, с помощью дифференциального уравнения неравномерного движения определить вид кривой и назначить начальную глубину.
3. Задаваясь количеством участков N=4 и шагом глубин 
, определить координаты и длину кривой свободной поверхности.
4. Построить на миллиметровке в масштабе продольный разрез по оси канала с указанием координат свободной поверхности, линий нормальных и критических глубин.
Расчет выполняем по способу М. Д. Чертоусова (х= 4).
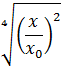
i > 0
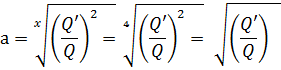
2.0 < x ≤ 5.5
Q=18 м/с
- параметр критичности, > 1 (бурное), < 1 (спокойное)
Определяем критические глубины.
= 0,998*0,71=0,71 м
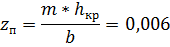
hнач = 1,02h0
0.98h0 – кривая спада
hкон = 1,5h0
h0 = 2,08 м
Расчет кривой подпоры.
| h, м |  h, м
|  , м2
| B, м |  , м
| R=  м
| C, м0,5/с | 
|
| 
| 1-
| z= 
| 
| Ф(z) | 
|  , м
| 
| l, м |
| 2,12 | 0,5 0,5 | 27,94 | 16,36 | 17,64 | 1,58 | 43,52 | 18,72 | 0,0295 | 0,0316 0,0303 | 0,9684 0,9697 | 1,02 | 0,22 0,21 | 1,55 | -0,55 -0,09 | 2,27 2,38 | 15866,67 15133,33 | 4714,88 11400,47 |
| 2,62 | 36,50 | 17,86 | 19,45 | 1,88 | 44,86 | 27,50 | 0,0311 | 1,24 | 1,00 | ||||||||
| 3,12 | 45,80 | 19,36 | 21,25 | 2,15 | 45,89 | 37,74 | 0,0322 | 1,45 | 0,91 | ||||||||
 =16115,35
|
Шлюз-регулятор-водослив с широким порогом.
При входе в трапецеидальный канал проектируется регулятор, работающий как прямоугольный водослив с широким порогом. Высота водослива p. При пропуске расчетного расхода Q глубина воды в канале перед водосливом равна hк, за водосливом – h0.
Требуется: определить ширину водослива b.
| Исходные данные | Вариант 2 |
| Расход Q, м3/с | |
| Глубина hб, м | 2,3 |
| Высота порога р, м | 0,3 |
| Исходные данные | Вариант 2 |
| Ширина канала bк, м | |
| Коэффициент заложения откоса mк, м | 1,5 |
| Глубина hк, м | 1,4hб |
; 
H=hк=1,4hб=1,4*2,3=3,22 м
Если регулятор стоит на плотине, то 
=0. 
р1=р2=0,3
m1=0,320, по таблице п. XIX
b/B=0
m2=0,325
mср=(0,320+0,325)/2=0,3225
р1/Н0=0,3/3,22=0,09
=hб-р=2,3-0,3=2
= 1 если = 0
Вывод:
Расчет плотины (водосливная часть) – водослив практического профиля криволинейного очертания.
Водосливная плотина практического профиля криволинейного очертания имеет n одинаковых пролетов с затворами на гребне водослива, поддерживающими НПУ (нормальный подпорный уровень). Ширина одного пролета b. За профилирующий принимается напор при НПУ. Скорость подхода к водосливу V0.
Требуется:
1. Определить отметку гребня водослива и его высоту из условия пропуска через открытые пролеты расчетного расхода Q при НПУ и заданной отметке уровня нижнего бьефа УНБ1.
2. Определить расход Qф через плотину при форсированном подпорном уровне ФПУ (затворы открыты) и уровне воды в нижнем бьефе УНБ2.
3. Вычислить координаты водосливной поверхности и поверхности потока при пропуске расхода Q и построить профиль плотины и свободной поверхности в масштабе на миллиметровке.
| Исходные данные | Вариант 2 |
| Расход Q, м3/с | |
| Ширина пролета b, м | |
| Число пролетов n | |
| Скорость V0, м/с | 1,4 |
| Исходные данные | Вариант 2 |
| Отметки: ФПУ, м НПУ, м Дно, м УНБ1 при НПУ, м УНБ2 при ФПУ, м |
УНБ < Гр ⇒ 
I. 1) 
а=0,11
m=0.49 (I тип водослива, Н=Нпр)
2) Уточняем первое приближение
3) 
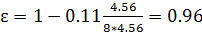
4) 
5) 
II. 
`Qф=1*0,95*0,5*8*8*4,43*5,563/2=1766 м3/с