Канторово множество
Возьмём отрезок [0;1] и разделим его на три равные части. Удалим средний интервал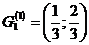 
.
Оставшиеся два отрезка вновь делим на три равные части и удаляем средние интервалы, т.е. интервалы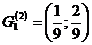 
и 
.
Осталось четыре отрезка. Каждый из них вновь делим на три равные части и удаляем средние интервалы, т.е. интервалы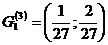 
, 
, 
, 
.
…………………………………………………………………………………………….
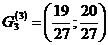Множество, оставшееся после счётного числа удалений, называется Канторовым множеством (обозначение К).
Для изучения арифметической структуры точек Канторова множества будем записывать числа из [0;1] в троичной системе. В этом случае концы удалённых интервалов и только они имеют два троичных представления.
Пример:
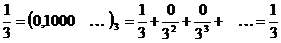
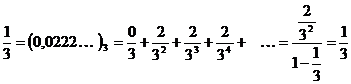
Таким образом, после первого удаления остаются точки, троичное разложение которых может быть записано так, что на первом месте стоит либо 0, либо 2 и т.д. В результате в Канторовом множестве находятся только те точки, троичное разложение которых может (для границ два представления) состоять из 0 и 2.
Свойства Канторова множества
1) Канторово множество имеет мощность континуума.
Доказательство:
Действительных точек в Канторовом множестве столько, сколько последовательностей из 0 и 2. Но последних столько же, сколько последовательностей из 0 и 1. Последовательностей из 0 и 1 континуум. Следовательно,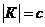 
.
Если точка является концом одного из смежных интервалов, то она называется точкой первого рода Канторова множества. Множество всех точек первого рода является счётным множеством.
Если же точка Канторова множества не является концом ни одного из смежных интервалов, то она называется точкой второго рода Канторова множества. Множество всех точек второго рода является множеством мощности континуума.
|
|
2) Канторово множество не содержит ни одного интервала.
Доказательство:
Вычислим сумму длин удалённых интервалов:
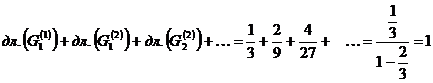
Отсюда в Канторовом множестве не может быть ни одного сплошного интервала.
Определение. Множество F называется совершенным, если F - замкнуто и не имеет изолированных точек.
Примеры:
[0;1] – совершенное множество;
(0;1] – не совершенное множество, т.к. оно не замкнуто;
- не совершенное множество, т.к. оно не замкнуто и содержит изолированные точки.
3) Канторово множество является совершенным множеством.
Доказательство:
1. Докажем, что Канторово множество замкнуто. Представим его следующим образом:
Множество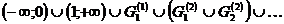 
открыто как объединение любого семейства открытых множеств. Тогда множество K замкнуто как дополнение к открытому множеству.
2. Покажем, что множество K не содержит изолированных точек.
Пусть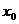 
– произвольная точка из множества K, 
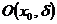- произвольная окрестность точки .
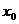Пусть число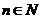 
таково, что 
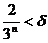. Запишем 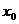в троичном разложении:
, где 
. Определим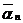 
следующим образом:
Рассмотрим число 
, 
. При этом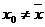 
, так как на n -ом месте в троичных разложениях 
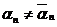. Найдём расстояние между точкам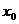и и 
:
,
,
получаем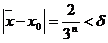 
(так как 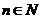мы подобрали таким образом, что 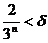). Отсюда 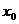не может быть изолированной точкой, так как существует точка , такая, что 
.
Таким образом, Канторово множество является совершенным множеством.
4. Мера Канторова множества равна нулю.
Пример: Определить, принадлежит ли Канторову множеству точка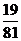 
.
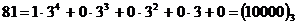
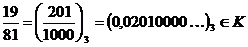
Мы получили, что точка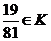 
и является точкой первого рода.
|
|
Тогда существует второе представление этой точки:
.
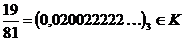Сделаем проверку:
.
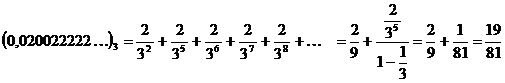