Краткая теоретическая информация
Вариационная пульсометрия - это один из методов анализа вариабельности сердечного ритма.
Данный подход является современной методологией и технологией исследования и оценки состояния регуляторных систем организма, в частности, функционального состояния различных отделов вегетативной нервной системы. Регуляция сердечного ритма в физиологических условиях является результатом ритмической активности пейсмекеров синусового узла (клеток, генерирующих электрическое возбуждение сердца) и модулирующего влияния вегетативной и центральной нервной систем, а так же ряда гуморальных и рефлекторных воздействий.
Методы изучения вариабельности сердечного ритма можно условно разделитьна три группы:
1) методы статистической оценки числового массива кардиоинтервалов;
2) методы оценки связи между кардиоинтервалами;
3) методы выявления скрытой периодичности динамического ряда кардиоинтервалов (Баевский, Кириллов, Клецкин.
Временные методы:
Временным методам относятся статистический анализ и геометрические методы, к частотным - спектральный анализ.
Наибольшее применение в России (СССР) за последние 30 лет получили следующие пять методов анализа ритма сердца:
1)Статистический анализ.
2) Вариационная пульсометрия - соответствует геометрическим методам по европейско-американским стандартам.
3) Автокорреляционный анализ.
4) Корреляционная ритмография.
5) Спектральный анализ. Эти методы являются наиболее распространенными, и в настоящее время накоплен большой опыт их применения в различных областях клинической медициныи прикладной физиологии.
В настоящей работе для оценки вариабельности сердечного ритма будет использован метод вариационной пульсометрии. Метод основан на установлении закона распределения кардиоинтервалов как случайных величин.
Использование в медицине:
Значения вариабельности сердечного ритма используются как важный
прогностический показатель, например в кардиологии, при оценке риска после острого инфаркта миокарда, при диагностике недостаточности кровообращения, при оценке риска внезапной смерти.
Показатели вариабельности сердечного ритма применяются также в других разделах медицинской практики для диагностик состояния пациента, для оценки степени тяжести состояния, для контроля за действием лекарственных препаратов и эффективностью проводимого лечения.
Кроме того, вариационная пульсометрия широко применяется в спортивной медицине для оценки состояния спортсмена при тренировках различной степени тяжести.
Достоинство метода вариационной пульсометрии заключается в простоте получения данных, высокой чувствительности метода, возможности получить количественную оценку состояния организма при нагрузках.
Анализ ритма сердца позволяют выявить его волновую структуру,
определенную периодичность в изменении продолжительности R-R интервалов.
Волновая периодика ритма отражает влияние на синусовый узел центрального и автономного контуров регуляции.
Анализ сердечного ритма методом вариационной пульсометрии позволяет дать количественно-качественную оценку текущего
функционального состояния организма, а также определить степень физической тренированности пациента.
По данным вариационной пульсометрии вычисляют такой широко
используемый показатель, как индекс напряжения регуляторных систем (Ин), который вычисляют следующим образом:
Ин = АMо/2*Mо*MxDMn.
Величина Ин в норме колеблется в пределах от 50 до 150 условных единиц. При эмоциональном стрессе и физической работе у здоровых людей значения Ин увеличиваются до 300 -500 единиц, а у людей старшего возраста со сниженными резервами такие значения наблюдаются даже в покое. При наличии стенокардии Ин достигает 600-700 единиц, а в предынфарктном состоянии даже 900-1100 единиц.
Случайные величины
Параметры, которые нельзя предсказать с высокой точностью, их величина в каждый момент времени для наблюдателя является случайным числом.
Случайные величины могут быть либо дискретными, либо непрерывными.
Дискретной называют случайную величину, принимающую определенные числовые значения. Например, число дождливых дней в году, число машин, проехавших через перекресток в течение суток, число пациентов, обратившихся к участковому врачу в
течение месяца и так далее.
Непрерывной, принимает любые значения из некоторого конечного или бесконечного интервала. Например, продолжительность жизни человека есть непрерывная случайная величина, так как она может быть определена с любой точностью (число прожитых лет; число лет и месяцев; число лет, месяцев и недель и т.д.)
В противоположность случайным величинам, значения параметров системы или процессов, которые можно точно предсказать в любой момент времени, называются детерминированными величинами или процессами.
Если для случайной дискретной величины каждому ее значению поставить в
соответствие вероятность ее появления, то такой ряд пар чисел называется рядом распределения. Например, для подброшенной монеты вероятности ее падения какой-либо стороной вверх будут – «орел» - 0,5; «решка» - 0,5.
Вероятность P того, что случайная величина X находится в интервале от - ∞ до x называется интегральной функцией распределения случайной величины F(x), то есть F (х)=Р {Х<=х}
Вероятность попадания случайной величины X в некоторый интервал от x 1 до x 2
может быть вычислена как разность значений интегральных функций распределения на границах интервала: P(x 1 <X<x 2) = F(x 2)-F(x 1). 1)
Одномерная дифференциальная функция распределения случайного процесса или плотность вероятности определяется равенством:
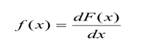 2)
2)
Таким образом, с учетом (2) формула (1) запишется в виде:
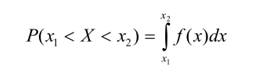
Числовые характеристики случайной величины
Любая случайная величина (непрерывная или дискретная) может быть
охарактеризована некоторыми числовыми параметрами, определяющими ее свойства.
1. Математическое ожидание М - ожидаемое среднее значение случайной
величины. Для дискретной случайной величины

где N – число значений случайного процесса X,
p i – вероятность каждого значения.
Если все значения равновероятны, p i =1/N для всех i.
Для непрерывной случайной величины
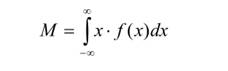
2. Дисперсия D - характеристика рассеяния случайной величины вокруг ее
среднего значения. Для дискретной случайной величины
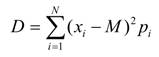
Для непрерывной:
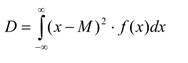
3. Удобной характеристикой рассеяния случайной величины является среднее квадратическое отклонение σ, равное:
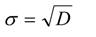
Математическая зависимость между значениями случайной величины и их вероятностями называется законом распределения. Существуют различные виды этих законов (нормальный, Пуассона, биномиальный и другие).
Нормальный закон распределения Гауса:
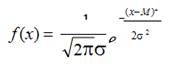
Как видно из формулы (6), нормальный закон распределения полностью
характеризуется двумя параметрами М и σ. Поэтому случайная величина, распределённая по нормальному закону, вполне может быть задана этими 2-мя параметрами.


Выражение определяет вероятность попадания на участок (x 1, х 2) случайной величины, распределенной по нормальному закону, через интегральную функцию распределения Ф(z), значение которой можно взять из таблиц.
Интегральная функция распределения Ф(z) для нормального закона имеет
свойства:
1. Ф(-∞) = 0; Ф (∞) = 1
2.Ф(-z) = 1- Ф(z)
3.Можно рассчитать вероятность попадания случайной величины X в данный
интервал: (М - σ, М + σ); (М - 2 σ; М + 2 σ); (М- З σ; М + З σ)
Р(М - σ < х < М + σ) = 0,68
Р(М-2 σ < х < М + 2 σ) = 0,95
Р(М - З σ < х < М + З σ) = 0,997
Таким образом, при нормальном распределении 68% значений случайной
величины лежат в пределах ± σ от среднего значения М, 95% в пределах от ± 2 σ от М, 99,7% в пределах ± З σ от М.
Для проверки гипотезы о соответствии закона распределения
случайной величины нормальному закону применяют критерий Пирсона.
Критерий Пирсона:
Достоинством критерия Пирсона является его универсальность: с его помощью можно проверять гипотезы о различных законах распределения. Для удобства ее обработки, разделим интервал от наименьшего до наибольшего из значений вариант на s равных частей. Будем считать, что значения вариант, попавших в каждый интервал, приближенно равны числу, задающему середину интервала.
Критерий в виде случайной величины:
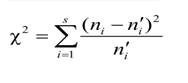
Можно доказать, что вне зависимости от реального закона распределения
генеральной совокупности закон распределения случайной величины (8) при
n → ∞ стремится к закону распределения с числом степеней свободы k = s – 1 – r, где
r– число параметров предполагаемого распределения, оцененных по данным выборки.
Нормальное распределение характеризуется двумя параметрами, поэтому k = s – 3.
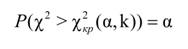
где α – уровень значимости. Следовательно, область принятия гипотезы о
нормальном законе распределения задается неравенством - х2 < х2кр (а,к)
Итак, для проверки гипотезы, что генеральная совокупность распределена
нормально – нужно вычислить по выборке наблюдаемое значение критерия:
