Основной задачей анализа движения (кинематики) звеньев плоских кулачковых механизмов является определение перемещения, скорости и ускорения ведомого звена по заданному очертанию профиля кулачка и функции движения ведущего звена. Решение этой задачи может быть осуществлено аналитическим и графическим методами.
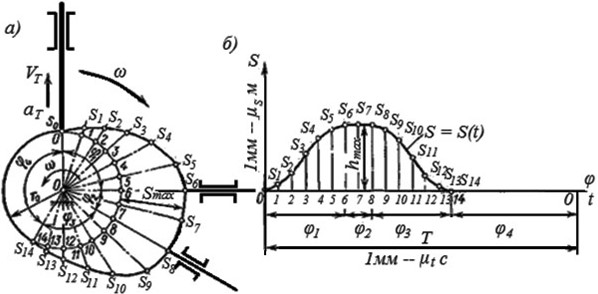
Рис. 5.2. Схема построения графика перемещения толкателя
Аналитический метод дает возможность более точно определять значения параметров кинематики в любой момент движения кулачка. Например, перемещение толкателя механизма, изображенного на рис. 5.1 б, может быть задано зависимостью S = S max · sin k φ, где S max – наибольшее перемещение толкателя; φ – угол поворота кулачка. В этом случае скорость толкателя VT = dS / dt = S max ·k ω · cos k φ, ускорение
(при ω = const) aT = dv / dt = S max ·k 2ω2 · sin k φ.
Графический метод менее точен, но он прост и нагляден, поэтому находит широкое применение. Сущность этого метода рассмотрим на следующем примере.
Построение плана положений механизма и графика перемещения толкателя. План положений может быть построен методом инверсии. (всему механизму мысленно сообщается вращение с угловой скоростью, угловой скорости кулачка ω, но противоположной по направлению.
Некоторые вопросы динамики кулачковых механизмов
Одной из важных задач динамики кулачковых механизмов является анализ сил и условий нормального взаимодействия звеньев. При этом существенное значение имеют угол давления и кпд механизма.
Понятие об угле давления. Пусть дан центральный кулачковый механизм.Положение точки А касания кулачка и толкателя относительно оси вращения кулачка определяется радиус-вектором ρ, величина которого
ρ= + ϕ r 0 S (), (5.1)
где r 0 – радиус основной шайбы кулачка; S (φ)– перемещение толкателя, соответствующее повороту кулачка на угол φ.
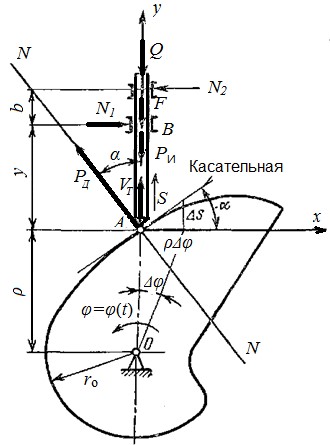
Схема сил в центральном кулачковом механизме
Движущая сила Р Д, действующая со стороны кулачка на толкатель, всегда совпадает с нормалью NN к профилю кулачка в точке А. Вектор этой силы и вектор скорости толкателя составляют угол α, углом давления. Величина угла давления может быть выражена следующим образом. Повернем кулачок на небольшой угол Δφ. Согласно, имеем tgα = Δ S /ρΔφили
dS 1 V T
tgα = ⋅ = ⋅[ ro + S ().ϕ ](5.2) d ϕ ro + S ()ϕ ω
Из выражения (5.2) следует, что угол давления α представляет собой переменную величину, зависящую от очертания профиля кулачка и угла поворота φ, и может изменяться от 0 до наибольшего значения αmax.
Изготовление профиля кулачка
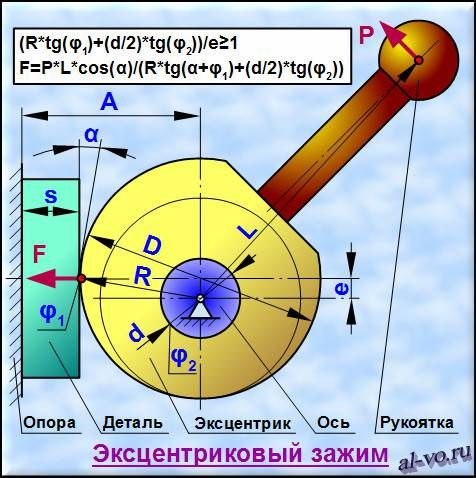
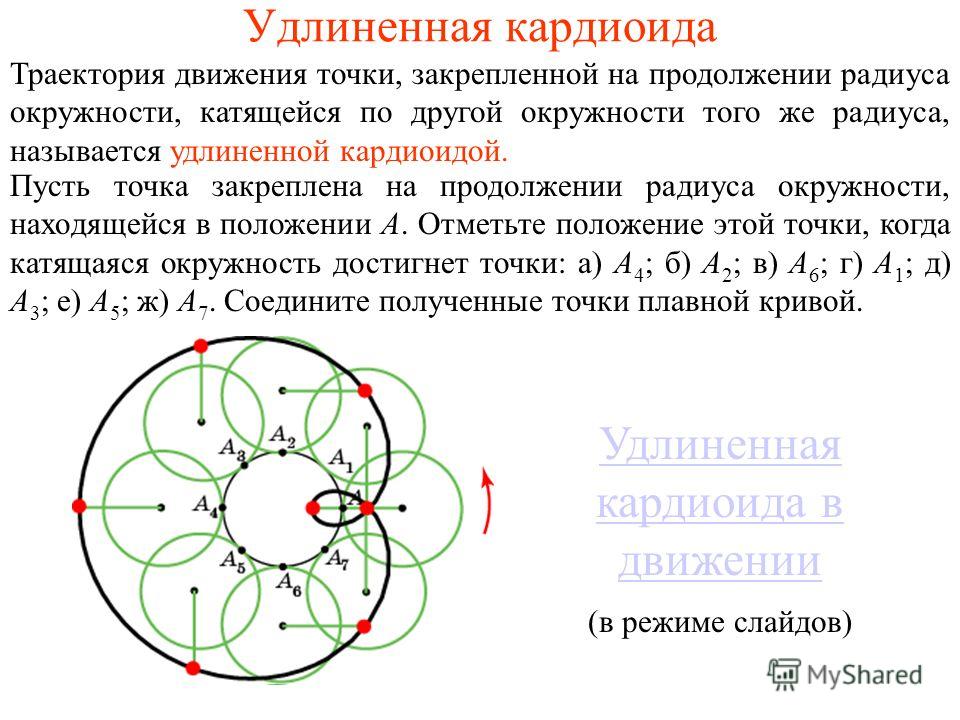
Двухползунный рычажный механизм,
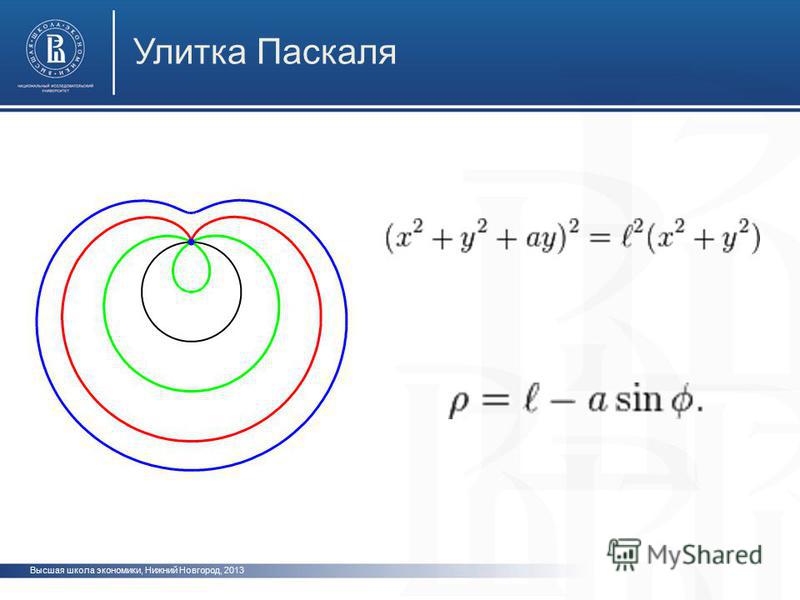
Механизм И. Кардана
(состоит из двух ползунов 1 и 3, связанных между собой шатуном2. Ползуны перемещаются по взаимно пересекающимся под углом β направляющим стойки0. Одна из точек шатуна (точка С) имеет траекторию в виде окружности радиусом r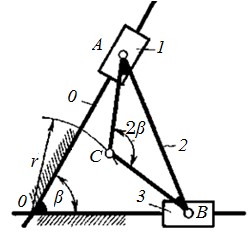 
, точки А и В движутся по прямым, а все остальные его точки – по эллипсам. Точка С является вершиной равнобедренного треугольника ABC, пристроенного к шатуну АВ. Угол при вершине С треугольника равен 2β, а боковые стороны – радиусу кривизны траектории точки С, т.е. ОС = АС = ВС. Угол β между осями направляющих чаще всего принимается равным 90°. Тогда точка С окажется на отрезке АВ и будет делить его пополам. Механизм И. Кардана является основой целого ряда прямолинейнонаправляющих механизмов приборов, механизма эллипсографа, и др.