Типовые задачи для самостоятельного решения

Типовые задачи с решениями и для самостоятельного решения

Типовые задачи с решениями

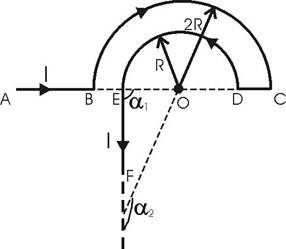
Задача 1. Бесконечно длинный провод с током I = 100 А изогнут так, как это показано на рисунке. Определить магнитную индукцию B в точке О. Радиус дуги R = 10 см.

Решение.

Магнитную индукцию B в точке O найдем, используя принцип суперпозиции магнитных полей: . В нашем случае провод можно разбить на пять частей: два прямолинейных провода AB и EF, уходящие одним концом в бесконечность, один отрезок DC и две полуокружности BC – радиусом 2R и DE – радиусом R. Тогда B=B_AB+B_BC+B_DC+B_DE+B_EF.

Магнитная индукция от участков AB и DC равна нулю, так как точка O лежит на оси провода AB. Поэтому B=B_BC+B_DE+B_EF.

Магнитная индукция поля кругового тока радиусом R равна , I – сила тока. Тогда и 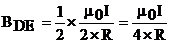. Причем вектор индукции B_BC направлен в сторону противоположную направлению вектора B_DE (из-за того что токи текут в разных направлениях). Вектор B_EF будет направлен в ту же сторону что и B_DE. Поэтому B=B_DE–B_BC +B_EF= .

Найдем B_EF. Известно, что магнитное поле на расстоянии r от отрезка длинной l, по которому течет ток силой I, равно . Поэтому в нашем случае магнитное поле от отрезка EF равно . Из рисунка видно, что α1= , α2=π, и r=R поэтому .

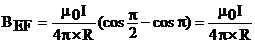Тогда магнитное поле от всей рамки равно .

Подставляем числа .

Задача 2. По двум скрещенным под прямым углом беско­нечно длинным проводам текут токи I и 2 I (I = 100 А). Определить магнитную индукцию B в точке А (рисунок). Расстояние d = 10 см.

Решение.

Магнитная индукция поля бесконечно длинного прямого тока на расстоянии r равна , I – сила тока.

Наша точка находится на расстоянии 2×d от первого провода и на расстоянии d от второго провода и тогда модули векторов магнитной индукции: , .

Из рисунка видно, что вектора B1 и B2 перпендикулярны друг другу, поэтому суммарный вектор магнитной индукции найдем по правилу Пифагора: .

Подставляем числа (переводя одновременно все величины в систему СИ). .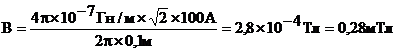

Задача 3. По тонкому кольцу радиусом R = 20 см течет ток I = 100 А. Определить магнитную индукцию B на оси кольца в точке А (рисунок). Угол α = π/3.

Решение.

Для решения задачи воспользуемся законом Био—Савара—Лапласа:

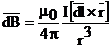, где dB — магнитная индукция поля, создаваемого элементом тока I×dl в точке, определяемой радиусом-векто­ром r.

Выделим на кольце элемент dl и от него в точку проведем радиус-вектор r (рис.). Вектор dB направим в соответствии с правилом буравчика.

Согласно принципу суперпозиции магнитных полей, магнитная индукция B в точке определяется интегри­рованием: , где интегрирование ведется по всем элементам dl кольца. Разложим вектор dB на две составляющие: dB₁, перпендикулярную плоскости кольца, и dB₂, параллель­ную плоскости кольца, т. е. .

Тогда . Заметив, что из соображений симметрии и что векторы dB₁ от различных элементов dl сонаправлены, заменим векторное суммирование (интегрирование) скалярным: 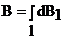, где dB₁=dB×cosα и (поскольку dl перпен­дикулярен r). Таким образом,

.

Из рисунка видно, что , откуда , поэтому

.

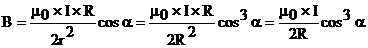Подставляем числа (переводя одновременно все величины в систему СИ). .

Типовые задачи для самостоятельного решения

1. Напряженность Н магнитного поля в центре кругового витка радиусом r = 8 см равна 30 А/м. Определить ток, текущий по витку

Рис. 1

Рис. 2

2. По бесконечно длинному проводу, изогнутому так, как это показано на рис. 1, течет ток I =200 А. Определить магнитную индукцию B в точке О. Радиус дуги R = 10 см.

3. По бесконечно длинному проводу, изогнутому так, как это показано на рис. 2, течет ток I = 200 А. Определить магнитную индукцию B в точке О. Радиус дуги R = 10 см.

4. Расстояние d между двумя длинными параллельными проводами равно 5 см. По проводам в одном направлении текут одинаковые токи I = 30 А каждый. Найти напряженность Н магнитного поля в точке, находящейся на расстоянии r ₁=4 см от одного и r ₂=3 см от другого провода.

Рис. 3

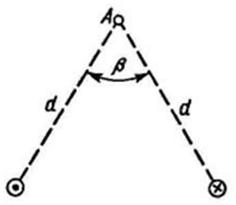Рис. 4

5. По тонкому кольцу течет ток I = 80 А. Определить магнитную индукцию B в точке A, равноудаленной от точек кольца на расстояние r = 10 см (рис. 3). Угол a = π/6.

6. По двум бесконечно длинным, прямым параллельным проводам текут одинаковые токи I = 60 А. Определить магнитную индукцию B в точке A (рис. 4), равноудаленной от проводов на расстояние d = 10 см. Угол = /2.

7. Бесконечно длинный провод с током I = 50 A изогнут так, как это показано на рис. 5. Определить магнитную индукцию B в точке A, лежащей на биссектрисе прямого угла на расстоянии d = 10 см от его вершины.

Рис. 5

Рис. 6

8. По двум скрещенным под прямым углом бесконечно длинным проводам текут токи I и 2 I (I = 100 А). Определить магнитную индукцию B в точке A (рис. 6). Расстояние d = 10 см.

Рис. 7

9. По двум бесконечно длинным проводам, скрещенным под прямым углом, текут токи I ₁ и I ₂ = 2 I ₁ (I ₁ = 100 А). Определить магнитную индукцию B в точке A, равноудаленной от проводов на расстояние d = 10 см (рис. 7).

10. По витку, имеющему форму квадрата со стороной а = 20 см, идет ток I = 5 А. Определите напряженность магнитного поля в точке пересечения диагоналей и в одной из точек пересечения сторон.