Граф называется гамильтоновым, если в нем имеется простой цикл, содержащий каждую вершину этого графа. Сам этот цикл также называется гамильтоновым. Гамильтоновой называют и простую цепь, содержащую каждую вершину графа. Слово «гамильтонов» в этих определениях связано с именем известного ирландского математика У. Гамильтона, которым в 1859 году предложена следующая игра «Кругосветное путешествие». Каждой из 20 вершин додекаэдра (рис. 1) приписано название одного из крупных городов мира.
рис. 2
Требуется, переходя от одного города к другому по ребрам додекаэдра, посетить каждый город в точности один раз и вернуться в исходный город.
Теорема Оре (О.Оре, 1960). Если для любой пары u и v несмежных вершин графа G порядка n≥3 выполняется неравенство deg u+deg v≥n, то G – гамильтонов граф.
Теорема Дирака (следствие теоремы Оре) (Г.Дирак,1952 г.). Если |G|=n≥3 и для любой вершины v графа G выполняется неравенство deg v≥n/2, то G – гамильтонов граф.
Лемма (о длине цикла)
Пусть 
- произвольный неориентированный граф и 
- минимальная степень его вершин. Если 
, то в графе существует цикл 
длиной 
.
Доказательство:
Рассмотрим путь максимальной длины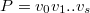 
. Все смежные с 
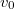вершины лежат на 
. Обозначим 
. Тогда 
. Цикл 
имеет длину 
Доказательство теоремы Дирака
Пусть - цикл наибольшей длины в графе . По лемме его длина . Если - гамильтонов, то теорема доказана. Предположим обратное, т. е. 
. Рассмотрим путь 
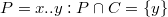наибольшей длины 
. Заметим, что по условию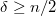 
, а значит 
и каждая вершина из 
смежна с некоторыми вершинами из . Заметим, что вершина 
не может быть смежна:
· с вершинами из , расстояние от которых до 
(по ) не превышает m. Действительно, пусть вершина 
и расстояние от 
до по циклу меньше либо равно . Тогда этот участок цикла можно заменить на 
, длина которого 
. Таким образом образуется цикл большей длины, что противоречит предположению о максимальности цикл .
|
|
· двум смежным вершинам на . Пусть 
и 
. Тогда заменив ребро 
на 
, увеличим длину цикла на 
.
· вершинам из 
, поскольку максимальный.
Получаем 
.
Противоречие.
граф теорема коммивояжер
Задача о коммивояжере
Историческая справка
Точно неизвестно, когда проблему коммивояжера исследовали впервые. Однако, известна изданная в 1832 году книга с названием «Коммивояжер — как он должен вести себя и что должен делать для того, чтобы доставлять товар и иметь успех в своих делах — советы старого курьера» в которой описана проблема, но математический аппарат для её решения не применяется. Зато в ней предложены примеры маршрутов для некоторых регионов Германии и Швейцарии.
Ранним вариантом задачи может рассматриваться игра Уильяма Гамильтона 19 века, которая заключалась в том, чтобы найти маршруты на графе с 20 узлами. Первые упоминания в качестве математической задачи на оптимизацию принадлежат Карлу Менгеру, который сформулировал её на математическом коллоквиуме в 1930 году так: «Мы называем проблемой посыльного (поскольку этот вопрос возникает у каждого почтальона, в частности, ее решают многие путешественники) задачу найти кратчайший путь между конечным множеством мест, расстояние между которыми известно.»
Вскоре появилось известное сейчас название задача странствующего торговца, которую предложил Гаслер Уитни из Принстонского университета.
|
|
Вместе с простотой определения и сравнительной простотой нахождения хороших решений задача коммивояжера отличается тем, что нахождение действительно оптимального пути является достаточно сложной задачей. Учитывая эти свойства, начиная со второй половины 20-го века, исследование задачи коммивояжера имеет не столько практический смысл, сколько теоретический в качестве модели для разработки новых алгоритмов оптимизации.
Многие современные распространенные методы дискретной оптимизации, такие как метод отсечений, ветвей и границ и различные варианты эвристических алгоритмов, были разработаны на примере задачи коммивояжера.
В 1950-е и 1960-е годы задача коммивояжера привлекла внимание ученых в США и Европе. Важный вклад в исследование задачи принадлежит Джорджу Данцигу, Делберту Рею Фалкерсону и Селмеру Джонсону, которые в 1954 году в институте RAND Corporation сформулировали задачу в виде задачи дискретной оптимизации и применили для ее решения метод отсечений. Используя этот метод, они построили путь коммивояжера для одной частной постановки задачи с 49 городами и обосновали его оптимальность. В 1960-е и 1970-е годы задача изучалась многими учеными как теоретически, так и с точки зрения ее приложений в информатике, экономике, химии и биологии.
Ричард Карп в 1972 году доказал NP-полноту задачи поиска гамильтоновых путей, из чего, благодаря полиномиальной сводимости, вытекала NP-трудность задачи коммивояжера. На основе этих свойств им было приведено теоретическое обоснование сложности поиска решений задачи на практике.
|
|
Больших успехов удалось достичь в конце 1970-х и 1980-х годах, когда Мартин Грётчел, Манфред Падберг и Джованни Ринальди и другие, с применением новых методов деления плоскостью, ветвей и границ вычислили решение для отдельного случая задачи с 2393 городами.
В 1990-е годы Дэвид Аплгейт, Роберт Биксби, Вашека Шватал и Уильям Кук установили рекорды по программе Конкорд. Герхард Райнельт создал TSPLIB — набор стандартизованных экземпляров задачи коммивояжера различной степени сложности для сравнения результатов работы различных групп исследователей. В марте 2005 года задача с 33 810 узлами была решена программой Конкорд: был вычислен путь длиной в 66 048 945 и доказано отсутствие более коротких путей. В апреле 2006 было найдено решение для экземпляра с 85 900 узлами. Используя методы декомпозиции, можно вычислить решения для случаев задачи с миллионами узлов, длина которых менее чем на 1 % больше оптимальной.